Файл: Практикум волгоград 2014 Печатается по решению редакционноиздательского совета.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 259
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Наиболее простая модель этой молекулы – отрезок спирали. Пусть на такую молекулу, диаметр витка которой равен а, падает линейно поляризованная волна 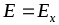 (рис.2). Она вызовет движение зарядов, направленное вдоль оси Х. Но если заряды будут двигаться вдоль спирали, то неизбежно возникнет их движение вдоль оси Y. Возникающее движение зарядов приведет к возбуждению Y - компоненты волны в Рис. 2
(рис.2). Она вызовет движение зарядов, направленное вдоль оси Х. Но если заряды будут двигаться вдоль спирали, то неизбежно возникнет их движение вдоль оси Y. Возникающее движение зарядов приведет к возбуждению Y - компоненты волны в Рис. 2
веществе, наличие которой должно привести к отклонению плоскости колебаний от направления Е=Ех Детальный расчет приводит к следующему результату для разности показателей преломления:
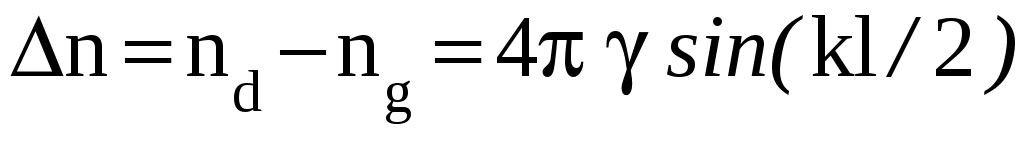 (11)
(11)
здесь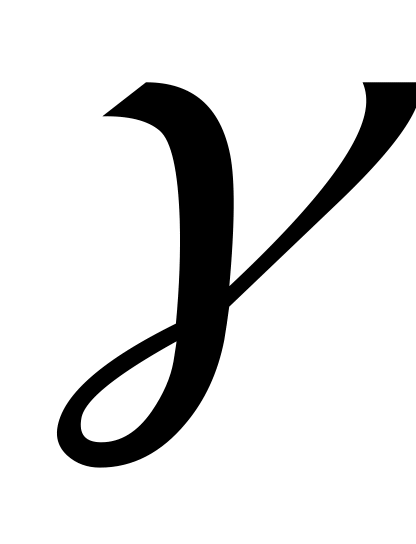 - некоторая постоянная, l - характерный размер молекулы оптически активного вещества. Таким образом, молекулярная теория позволяет объяснить различие в скоростях распространения волн, поляризованных по правому и левому кругу, что является существенным моментом в объяснении явления вращения плоскости поляризации.
- некоторая постоянная, l - характерный размер молекулы оптически активного вещества. Таким образом, молекулярная теория позволяет объяснить различие в скоростях распространения волн, поляризованных по правому и левому кругу, что является существенным моментом в объяснении явления вращения плоскости поляризации.
2.Описание установки.
Лабораторная установка (рис. 3) состоит из монохроматора (1), ртутной лампы (2), предназначенной для градуировки монохроматора, пульта питания (3), двух окулярных насадок к монохроматору - с ножом (4) и со щелью (5). Первая используется при градуировке, вторая - при измерениях.
Рис. 3. Схема лабораторной установки
О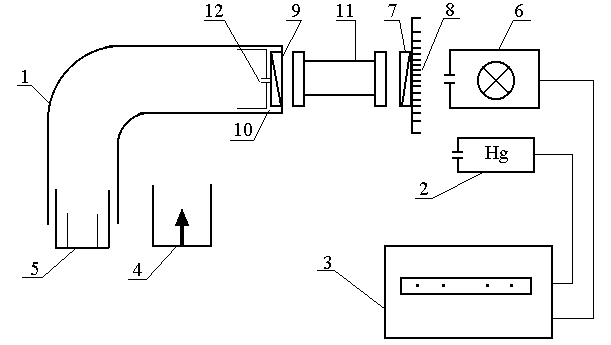
светитель (6) служит источником сплошного спектра. На нем укреплен вращающийся поляризатор (7) с лимбом и нониусом (8). Анализатор (9) вмонтирован во входное окно (10) монохроматора. Он неподвижен. Исследуемый раствор находится в кювете (11). При градуировке входная щель (12) монохроматора должна быть предельно малой (0.01 - 0.02 мм); при работе - полностью открытой. Для уменьшения фоновой засветки раствора желательно, чтобы оптические оси источника света, кюветы и входной трубы монохроматора совпадали. Однако, в процессе работы переюстировка запрещается.
3. Порядок выполнения работы
В настоящей работе исследуется вращение плоскости поляризации раствором активного вещества (сахарозы С12
Н22О11 в оптически нейтральном растворителе).
3.1. Используя формулу построить теоретическую зависимость постоянной врашения от длины волны для видимой области спектра в диапазоне от 400 Ả до 800 Ả с интервалом 25 Ả, полагая l = 10 Ả,
построить теоретическую зависимость постоянной врашения от длины волны для видимой области спектра в диапазоне от 400 Ả до 800 Ả с интервалом 25 Ả, полагая l = 10 Ả,  = 0.019 град·см2/г. Построение выполнить заранее в процессе домашней подготовки к работе.
= 0.019 град·см2/г. Построение выполнить заранее в процессе домашней подготовки к работе.
3.2. Произвести градуировку монохроматора. Для этого:
3.2.1. Установить ртутную лампу на рельсе и совместить оптические оси источника излучения и входной трубы монохроматора. Для увеличения интенсивности спектра поместить между ртутной лампой и монохроматором конденсор.
3.2.2. Добиться четкого изображения источника в центре колпачка на входной трубе, меняя положение лампы и конденсора на рельсе.
3.2.3. Укрепить на спектроскопе окулярную насадку с ножом.
3.2.4. Навести окуляр на резкость по ножу.
3.2.5. Ориентируясь на желтый дублет ртути (5770 Ả и 5790 Ả), отождествить ртутный спектр с указанным в атласе.
3.2.6. Произвести градуировку прибора (снять зависимость между показаниями барабана и длиной волны для каждой наблюдаемой линии ртутного спектра), взять не менее 25 точек во всех областях видимого спектра.
3.2.7. Построить градуировочный график.
3.3. Используя метод скрещенных поляризаторов, получить зависимость угла поворота плоскости поляризации от длины волны излучения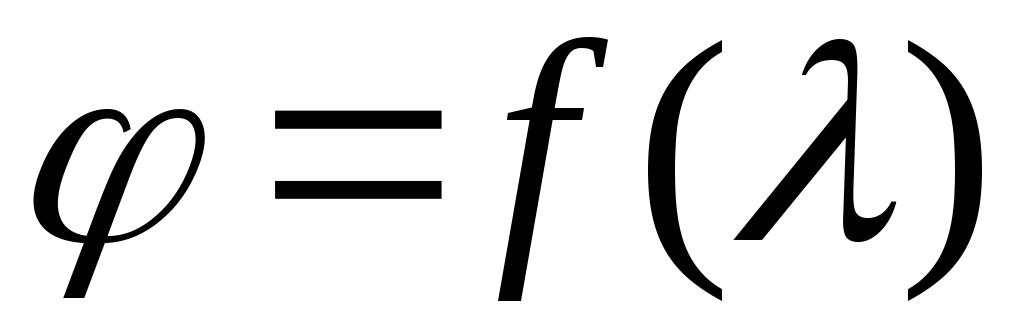 .
.
3.3.1. Заменить ртутную лампу источником сплошного спектра.
3.3.2. Совместить оптические оси входной трубы монохроматора и осветителя.
3.3.3. Укрепить на монохроматоре окулярную насадку со щелью.
3.3.4. Вращением поляризатора добиться минимального значения интенсивности, при этом отсчет по лимбу поляризатора принять за нулевой.
3.3.5. Установить между поляроидами кювету с исследуемым раствором.
3.3.6. Вращая поляризатор, добиться вновь минимального значения интенсивности для последовательных положений барабана монохроматора с шагом, соответствующим изменению длины волны излучения на 50 Ả За угол поворота плоскости поляризации φ принять разницу положений поляризатора (по лимбу).
3.4. Пересчитать зависимость
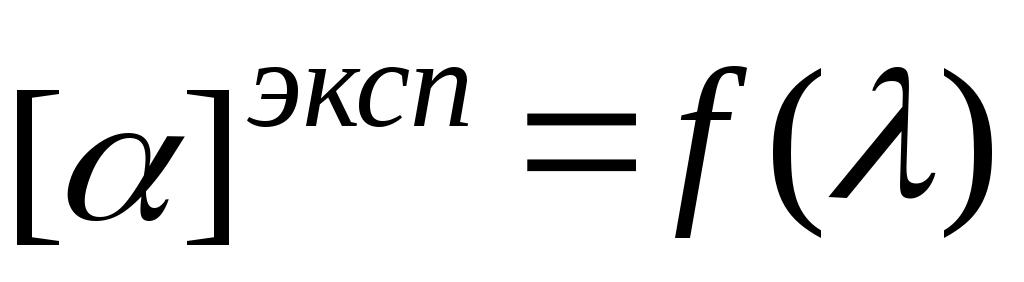 по формуле
по формуле 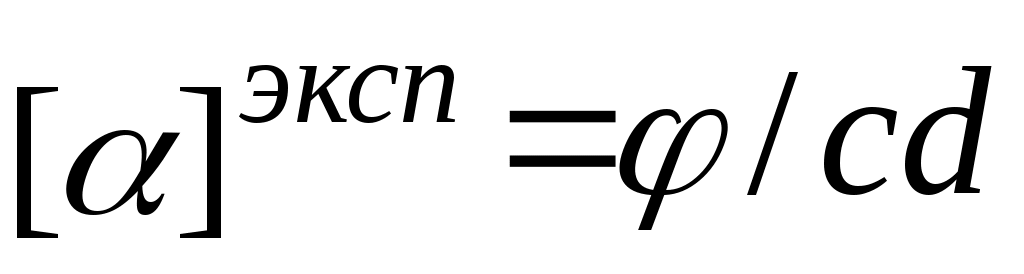
при d= 20 см, c= 0.87 г/см3.
3.5. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.6. На одной координатной сетке построить экспериментальные и теоретические зависимости постоянной вращения от длины волны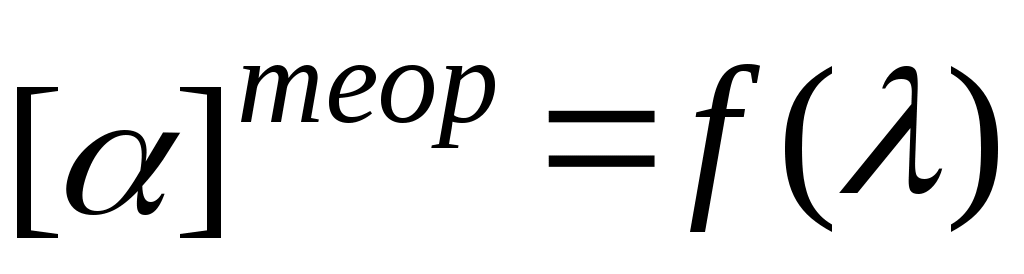 и
и 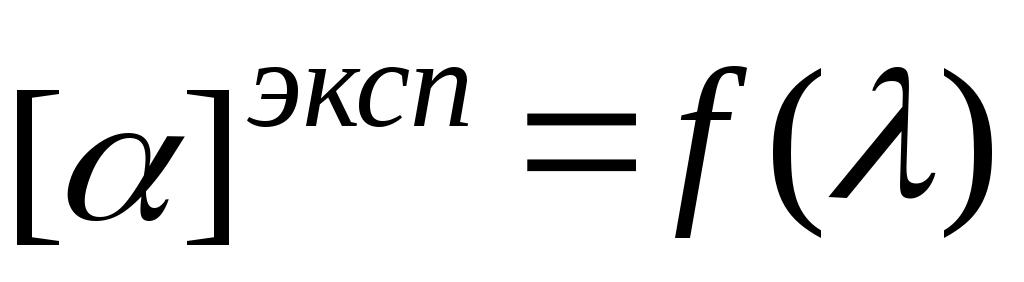 .
.
4. Контрольные вопросы и задания
1. В чем отличие поляризованного света от неполяризованного ?
2. Как отличить свет, поляризованный по кругу, от естественного света ?
3. Описать характер поляризации плоской монохроматической световой волны в зависимости от отношения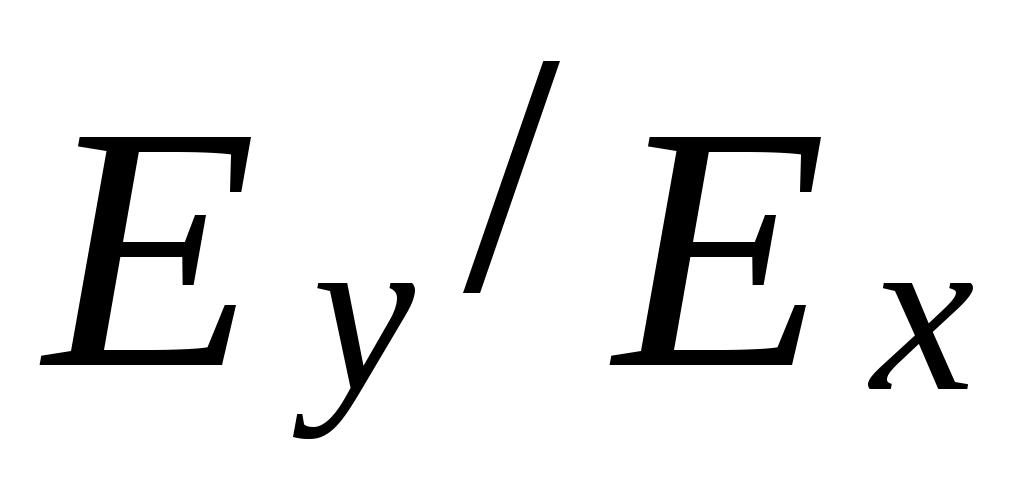 компонент комплексной амплитуды - электрического поля волны.
компонент комплексной амплитуды - электрического поля волны.
4. Описать установку, предложенную Френелем для экспериментального доказательства существования в одной из модификаций кристалла кварца двух циркулярно поляризованных волн.
5. Дать свои соображения относительно прямо пропорциональной зависимости угла поворота плоскости поляризации в растворах оптически активных веществ от концентрации последних.
6. Рассмотреть случай, когда падающий на активное вещество линейно поляризованный свет направлен под углом 45° к оси Х. Провести анализ вращения плоскости поляризации.
7. Пластинка кварца толщиной в 1 мм вырезана перпендикулярно к оптической оси и помещена между скрещенными николями. Будет ли пластинка оставаться освещенной при любой, длине волны падающего света из видимого диапазона? Объясните возникающее явление.
8. Какую минимальную разность показателей преломления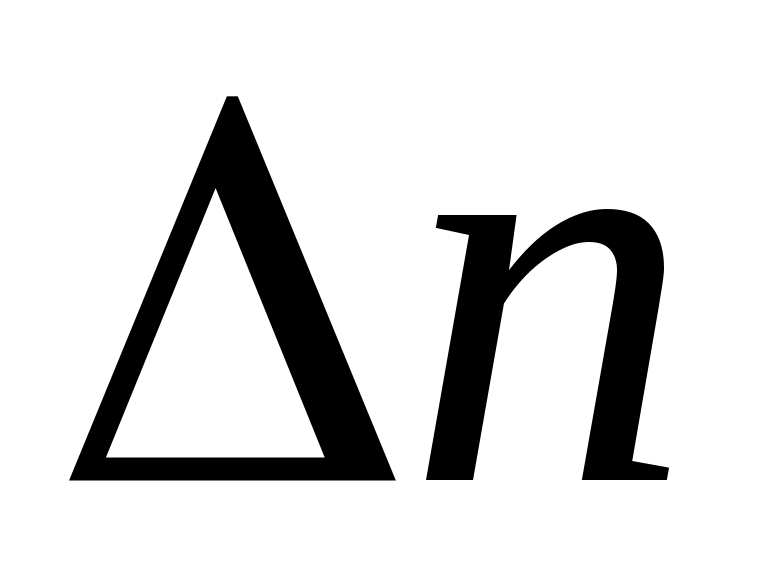 право- и левополяризованных по кругу волн (
право- и левополяризованных по кругу волн (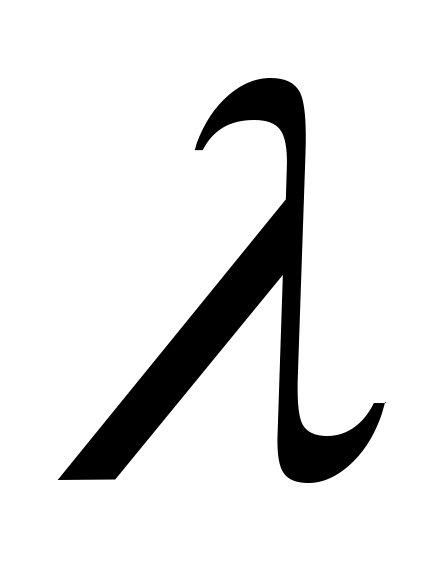 = 5893 А°) можно обнаружить при слое вещества l = 30 см, если измерять угол поворота плоскости поляризации с точностью 1° ?
= 5893 А°) можно обнаружить при слое вещества l = 30 см, если измерять угол поворота плоскости поляризации с точностью 1° ?
9. Объяснить действие поляризационной призмы Николя. Определить степень поляризации выходящего из призмы излучения при падении на нее естественного света.
10. Сравните действие поляроидной пластинки на поляризованное излучение маломощного непрерывного лазера и на естественный свет (в последнем случае для контроля поляризации применить два скрещенных поляроида).
11. Оценить степень поляризации прошедшего света, отраженного под углом Брюстера от стеклянной пластинки. Падающий свет – естественный.
12. Ветровое стекло и фары автомашины иногда снабжаются пластинками из поляроида. Как должны быть расположены эти пластины, чтобы шофер мог видеть дорогу, освещенную светом его фар, и не страдал от света фар встречных машин? Возможна ли, ситуация, когда при включенных фарах машин водители не увидят машину, едущую навстречу, и произойдет автомобильная катастрофа? Объяснение дать на основании законов оптики.

10 мкм). Поэтому в данном случае речь идет об интерференции в тонких пленках.
веществе, наличие которой должно привести к отклонению плоскости колебаний от направления Е=Ех Детальный расчет приводит к следующему результату для разности показателей преломления:
здесь
2.Описание установки.
Лабораторная установка (рис. 3) состоит из монохроматора (1), ртутной лампы (2), предназначенной для градуировки монохроматора, пульта питания (3), двух окулярных насадок к монохроматору - с ножом (4) и со щелью (5). Первая используется при градуировке, вторая - при измерениях.
Рис. 3. Схема лабораторной установки
О

светитель (6) служит источником сплошного спектра. На нем укреплен вращающийся поляризатор (7) с лимбом и нониусом (8). Анализатор (9) вмонтирован во входное окно (10) монохроматора. Он неподвижен. Исследуемый раствор находится в кювете (11). При градуировке входная щель (12) монохроматора должна быть предельно малой (0.01 - 0.02 мм); при работе - полностью открытой. Для уменьшения фоновой засветки раствора желательно, чтобы оптические оси источника света, кюветы и входной трубы монохроматора совпадали. Однако, в процессе работы переюстировка запрещается.
3. Порядок выполнения работы
В настоящей работе исследуется вращение плоскости поляризации раствором активного вещества (сахарозы С12
Н22О11 в оптически нейтральном растворителе).
3.1. Используя формулу
 построить теоретическую зависимость постоянной врашения от длины волны для видимой области спектра в диапазоне от 400 Ả до 800 Ả с интервалом 25 Ả, полагая l = 10 Ả,
построить теоретическую зависимость постоянной врашения от длины волны для видимой области спектра в диапазоне от 400 Ả до 800 Ả с интервалом 25 Ả, полагая l = 10 Ả, 3.2. Произвести градуировку монохроматора. Для этого:
3.2.1. Установить ртутную лампу на рельсе и совместить оптические оси источника излучения и входной трубы монохроматора. Для увеличения интенсивности спектра поместить между ртутной лампой и монохроматором конденсор.
3.2.2. Добиться четкого изображения источника в центре колпачка на входной трубе, меняя положение лампы и конденсора на рельсе.
3.2.3. Укрепить на спектроскопе окулярную насадку с ножом.
3.2.4. Навести окуляр на резкость по ножу.
3.2.5. Ориентируясь на желтый дублет ртути (5770 Ả и 5790 Ả), отождествить ртутный спектр с указанным в атласе.
3.2.6. Произвести градуировку прибора (снять зависимость между показаниями барабана и длиной волны для каждой наблюдаемой линии ртутного спектра), взять не менее 25 точек во всех областях видимого спектра.
3.2.7. Построить градуировочный график.
3.3. Используя метод скрещенных поляризаторов, получить зависимость угла поворота плоскости поляризации от длины волны излучения
3.3.1. Заменить ртутную лампу источником сплошного спектра.
3.3.2. Совместить оптические оси входной трубы монохроматора и осветителя.
3.3.3. Укрепить на монохроматоре окулярную насадку со щелью.
3.3.4. Вращением поляризатора добиться минимального значения интенсивности, при этом отсчет по лимбу поляризатора принять за нулевой.
3.3.5. Установить между поляроидами кювету с исследуемым раствором.
3.3.6. Вращая поляризатор, добиться вновь минимального значения интенсивности для последовательных положений барабана монохроматора с шагом, соответствующим изменению длины волны излучения на 50 Ả За угол поворота плоскости поляризации φ принять разницу положений поляризатора (по лимбу).
3.4. Пересчитать зависимость
при d= 20 см, c= 0.87 г/см3.
3.5. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.6. На одной координатной сетке построить экспериментальные и теоретические зависимости постоянной вращения от длины волны
4. Контрольные вопросы и задания
1. В чем отличие поляризованного света от неполяризованного ?
2. Как отличить свет, поляризованный по кругу, от естественного света ?
3. Описать характер поляризации плоской монохроматической световой волны в зависимости от отношения
4. Описать установку, предложенную Френелем для экспериментального доказательства существования в одной из модификаций кристалла кварца двух циркулярно поляризованных волн.
5. Дать свои соображения относительно прямо пропорциональной зависимости угла поворота плоскости поляризации в растворах оптически активных веществ от концентрации последних.
6. Рассмотреть случай, когда падающий на активное вещество линейно поляризованный свет направлен под углом 45° к оси Х. Провести анализ вращения плоскости поляризации.
7. Пластинка кварца толщиной в 1 мм вырезана перпендикулярно к оптической оси и помещена между скрещенными николями. Будет ли пластинка оставаться освещенной при любой, длине волны падающего света из видимого диапазона? Объясните возникающее явление.
8. Какую минимальную разность показателей преломления
9. Объяснить действие поляризационной призмы Николя. Определить степень поляризации выходящего из призмы излучения при падении на нее естественного света.
10. Сравните действие поляроидной пластинки на поляризованное излучение маломощного непрерывного лазера и на естественный свет (в последнем случае для контроля поляризации применить два скрещенных поляроида).
11. Оценить степень поляризации прошедшего света, отраженного под углом Брюстера от стеклянной пластинки. Падающий свет – естественный.
12. Ветровое стекло и фары автомашины иногда снабжаются пластинками из поляроида. Как должны быть расположены эти пластины, чтобы шофер мог видеть дорогу, освещенную светом его фар, и не страдал от света фар встречных машин? Возможна ли, ситуация, когда при включенных фарах машин водители не увидят машину, едущую навстречу, и произойдет автомобильная катастрофа? Объяснение дать на основании законов оптики.

ИНТЕРФЕРЕНЦИЯ СВЕТА
Лабораторная работа
ИНТЕРФЕРЕНЦИЯ СФЕРИЧЕСКИХ ВОЛН
(БИПРИЗМА ФРЕНЕЛЯ)
ЦЕЛЬ РАБОТЫ: изучение явления двухлучевой интерференции с помощью бипризмы Френеля, определение длины световой волны с использование данной интерферометрической схемы.
ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, две линзы (собирающая и рассеивающая), бипризма Френеля, экран, линейка, оптическая скамья с набором рейтеров.
1. Теоретическая часть [1¸6]
1.1. Интерференция волн
В эксперименте возможна ситуация, когда интенсивность света, создаваемая какими-либо двумя источниками, не равна сумме интенсивностей отдельных источников. Оказывается, что если свет от одного источника разделить прибором на два пучка и заставить их проходить разные пути, а затем наложить их друг на друга, то интенсивность их в области суперпозиции пучков будет изменяться от точки к точке. Она может достигать максимума, превышающего сумму интенсивностей пучков, и минимума, который может оказаться равным нулю. Это явление называется интерференцией. Оказывается, что при суперпозиции пучков строго монохроматического света интерференция возникает всегда. Однако, свет от физических источников никогда не бывает строго монохроматическим. Как следует из теории излучения атома, его амплитуда и фаза флуктуируют непрерывно и так быстро, что ни глаз, ни быстрый физический детектор не могут уследить за их изменениями.
Если две световых волны происходят от одного источника, то возникающие в них флуктуации амплитуды и фазы, вообще говоря, коррелированы, и о таких волнах говорят, что они полностью или частично когерентны, в зависимости от того, будет ли эта корреляция полной или частичной. В общем случае колебания (или волны) называются когерентными, если разность их фаз остается постоянной (или изменяется по определенному закону) во времени. В световых пучках от разных источников флуктуации совершенно независимы и пучки, как говорят, взаимно некогерентны. При наложении таких пучков от независимых источников интерференция в обычных экспериментальных условиях не наблюдается. Детальный анализ показывает, что «степень корреляции» между флуктуациями в двух световых пучках определяет «четкость» интерференционных эффектов, возникающих при суперпозиции пучков и, наоборот, «степень корреляции» сама определяется этими эффектами.
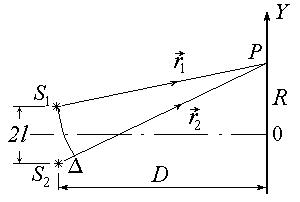
Рис.1
Рассмотрим вначале классическую схему Юнга наблюдения интерференционной картины для простейшего случая двух гармонических волн. Пусть два точечных источника S1 и S2 , расположенных на расстоянии 2l друг от друга излучают две монохроматические сферические когерентные волны 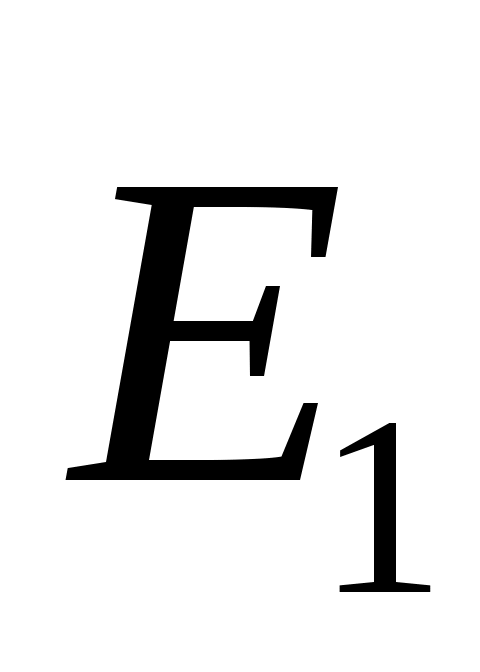 и
и 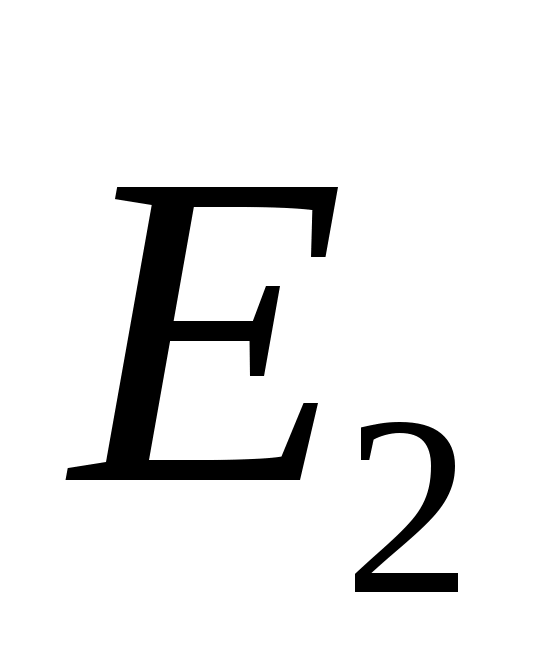 (рис.1). Предположим, что расстояние D от источников до экрана значительно больше 2l и положим для простоты, что амплитуды волн E1и E2в точке Р одинаковы и равны Е0 . Найдем результирующую амплитуду волн в точке Р, если
(рис.1). Предположим, что расстояние D от источников до экрана значительно больше 2l и положим для простоты, что амплитуды волн E1и E2в точке Р одинаковы и равны Е0 . Найдем результирующую амплитуду волн в точке Р, если
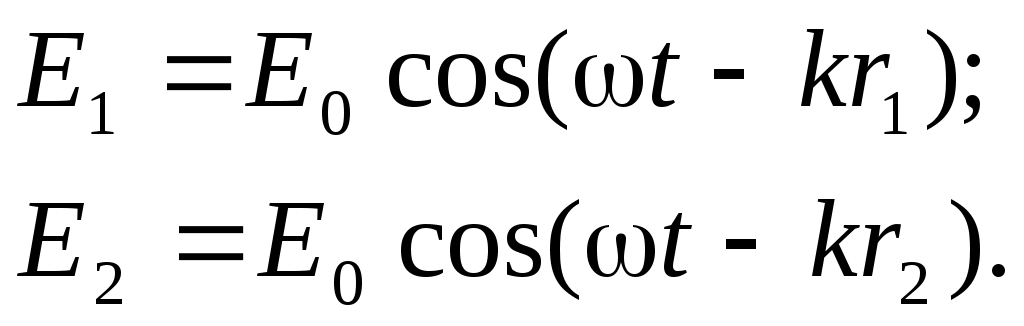 (1)
(1)
Тогда суммарная волна в точке Р:
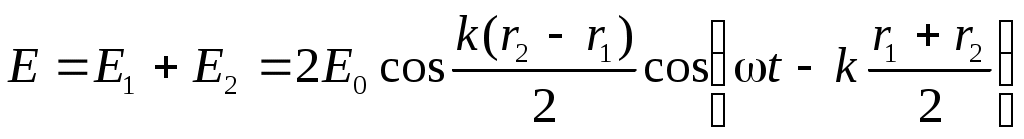 . (2)
. (2)
Введем величину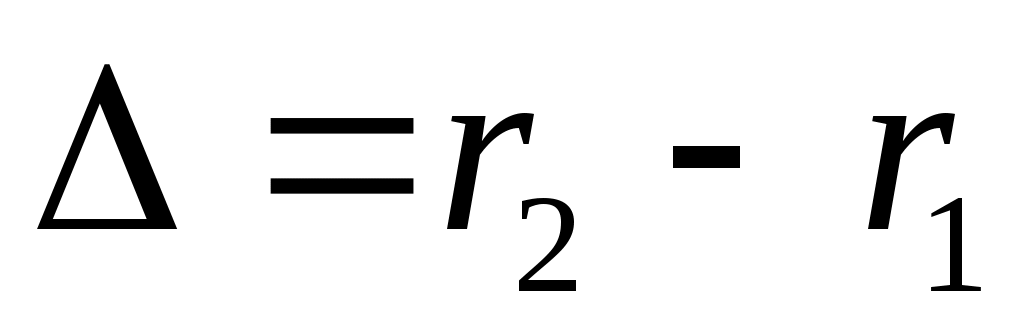 , называемую геометрической разностьюхода. Тогда интенсивность света будет равна:
, называемую геометрической разностьюхода. Тогда интенсивность света будет равна:
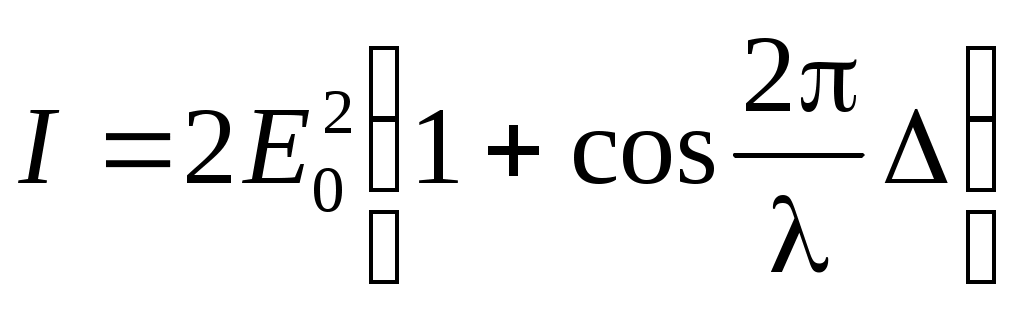 . (3)
. (3)
Видим, что
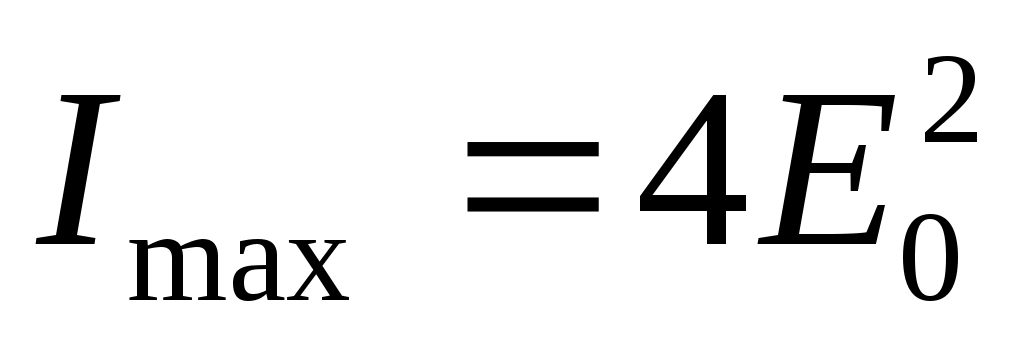 при
при 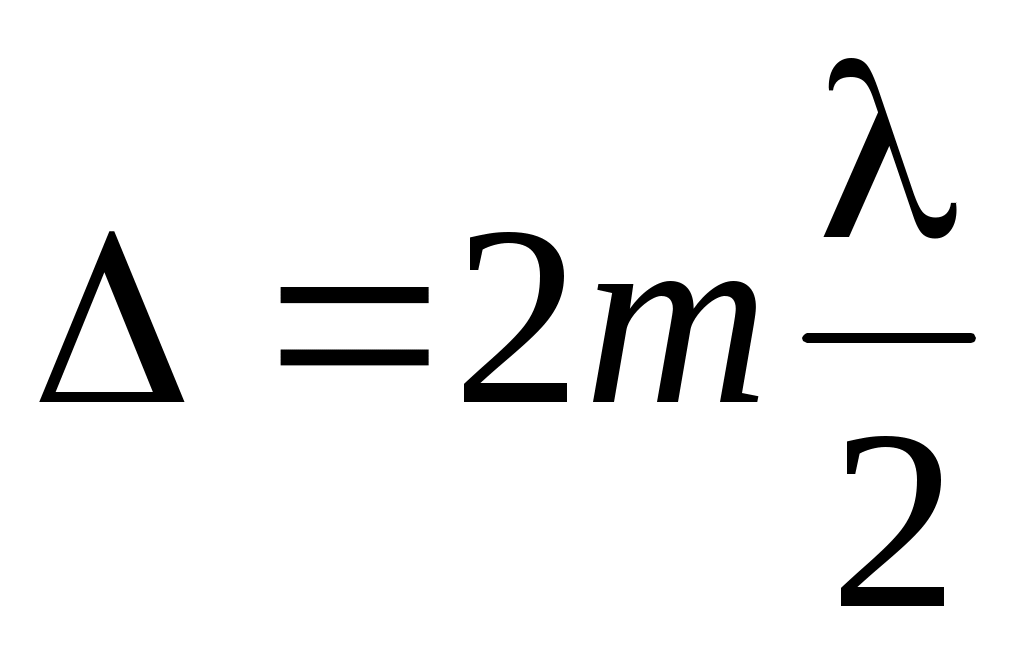 ; (4)
; (4)
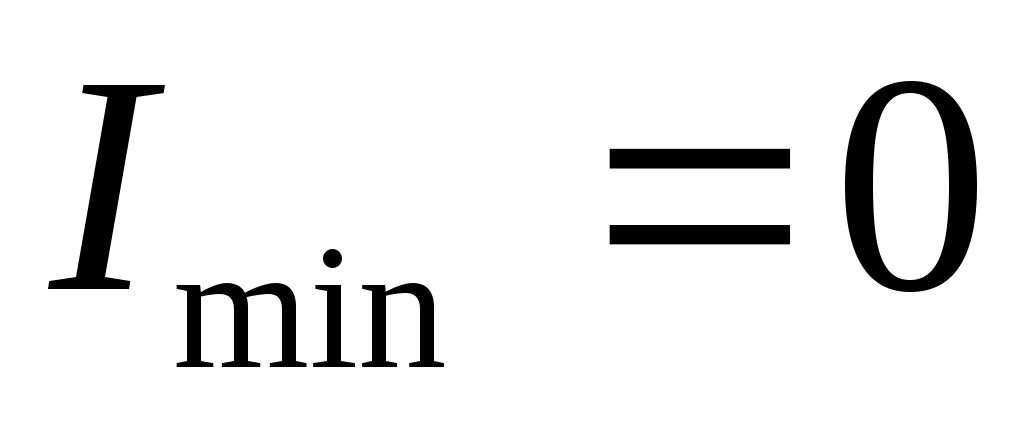 при
при 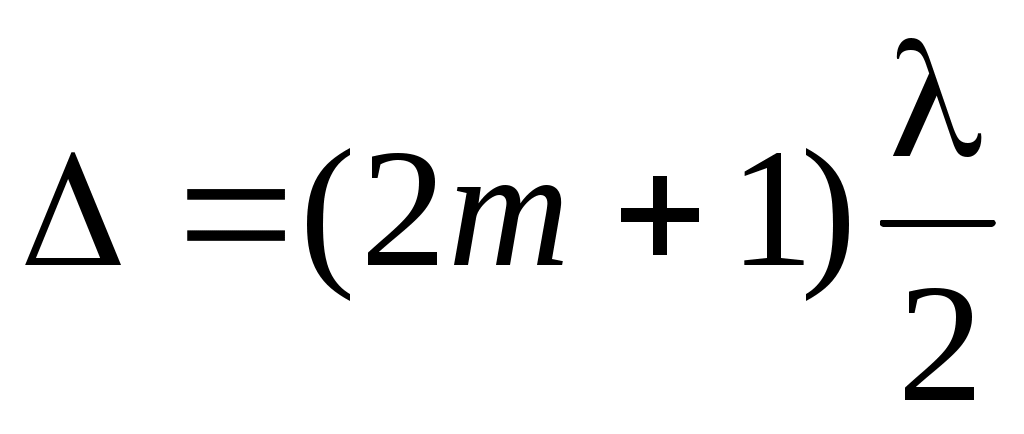 . (5)
. (5)
Таким образом, в результате наложения двух когерентных волн мы будем наблюдать в пространстве (или на экране, как это делается в эксперименте) чередующуюся в зависимости от разности хода картину максимумов и минимумов, называемую интерференционными полосами.
1.2. Получение когерентных световых волн с помощью бипризмы Френеля
Для получения когерентных световых волн от реальных источников пользуются следующим искусственным приемом. Волновой фронт разделяют на несколько частей. Полученные таким образом волны проходят различные оптические пути и при дальнейшем сложении уже обладают разностью хода, оставаясь когерентными. Потому, что разность хода зависит только от конструкции прибора.
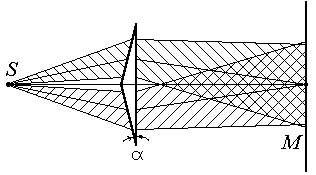
Рис.2
На рис. 2 приведен способ деления фронта волны на две части с помощью бипризмы Френеля. Важно отметить, что в практических приборах разность хода не делается обычно больше 100 ¸ 200 мм, т.к. длительность излучения атома
10-8 с, и при большой разности хода может случиться, что будут складываться волны, полученные уже от разных актов испускания, т.е. когерентность нарушится. Бипризма Френеля имеет малые преломляющие углы (a = 30/ ) и разность хода, приобретаемая волнами здесь мала. После преломления в бипризме падающий пучок света разделяется на два когерентных пучка с источниками в мнимых изображениях S‘ и S“ источника S (рис.3). Вычислим разность хода волн, приходящих в точку Р, через геометрические размеры оптической схемы.
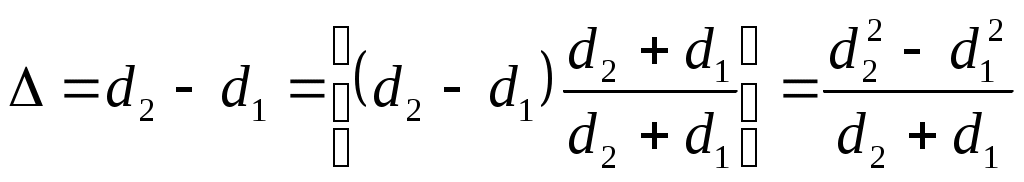 . (6)
. (6)
Считая, что в практических схемах d » D, ОР = y«D и следовательно: 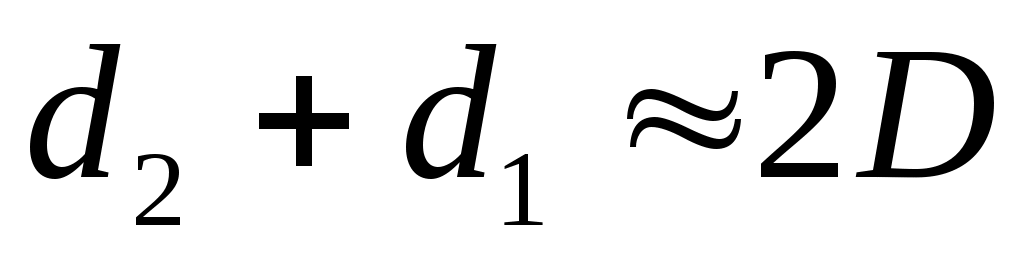 , получим:
, получим:
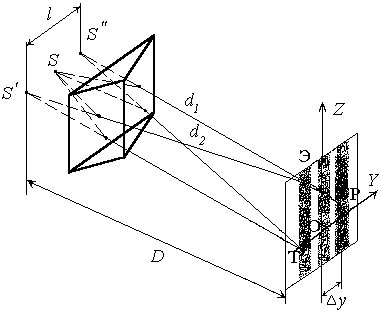
Рис.3
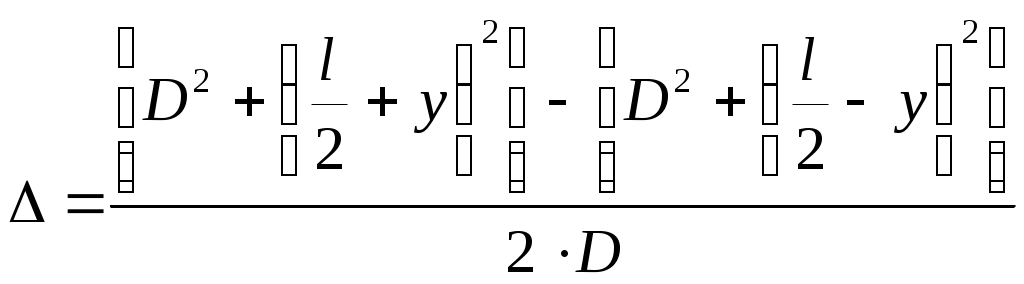 (7)
(7)
Преобразуя (7), получим:
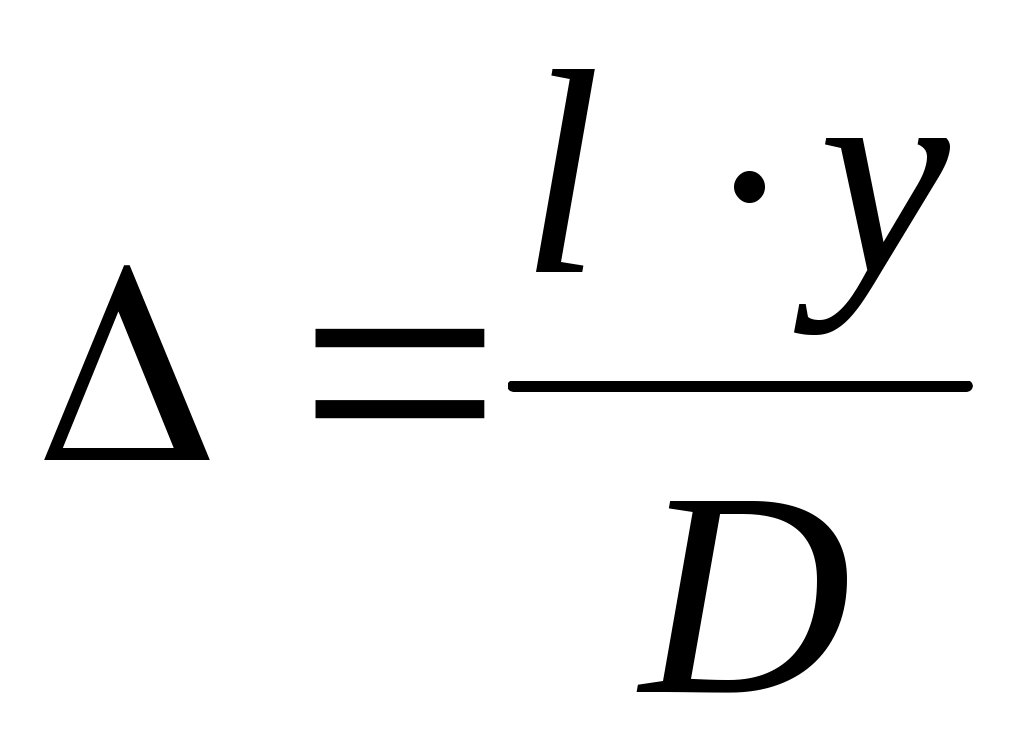 (8)
(8)
Пользуясь условием (4), при котором получается максимум интенсивности на экране, находим:
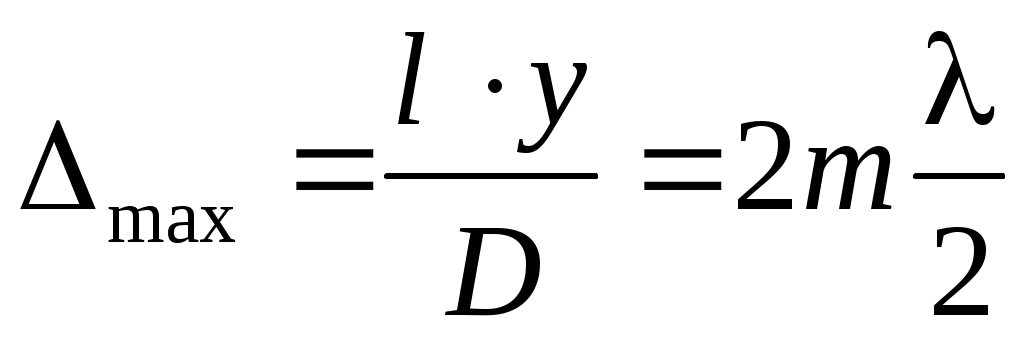 ; (9)
; (9)
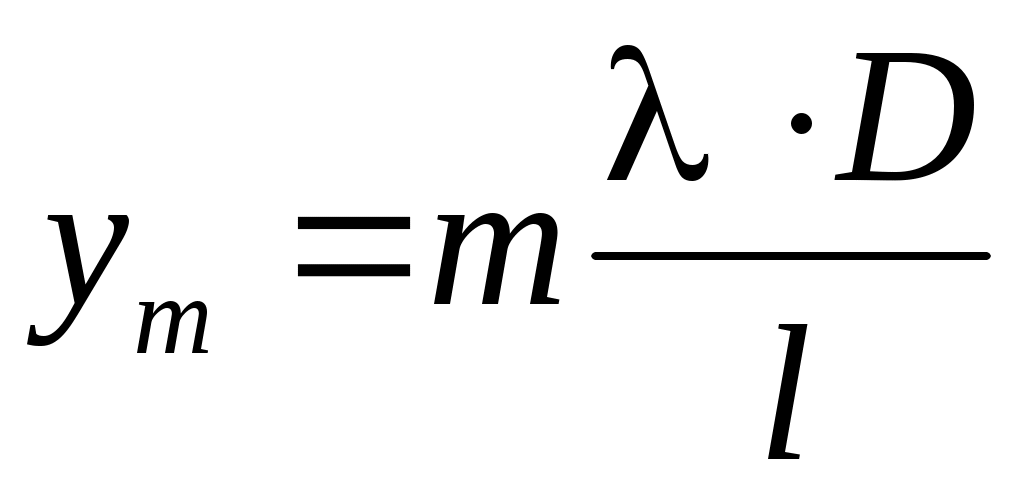 . (10)
. (10)
Соотношение (10) показывает, что максимумы отстоят друг от друга на равных расстояниях. Обозначая расстояние, соответствующее одному из максимумов ym, а следующему ym+1, получим:
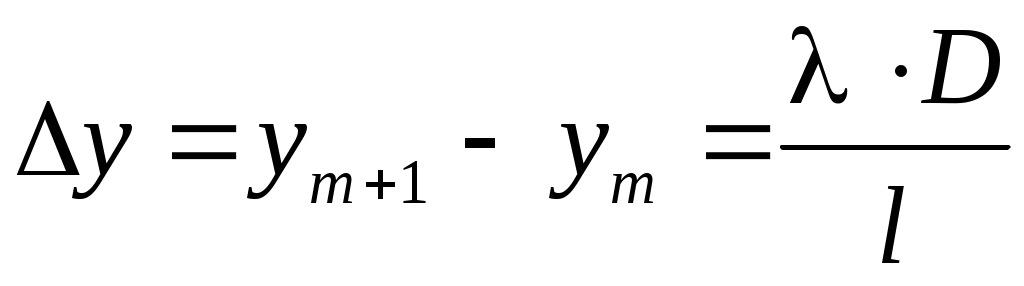 . (11)
. (11)
2. Описание установки
2.1. Определение длины световой волны с помощью бипризмы Френеля
Лабораторная установка (рис.4) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), короткофокусной собирающей линзы с фокусным расстоянием f1= 1 см (3), бипризмы Френеля (4) и экрана (5). Все элементы установлены на оптической скамье (6).
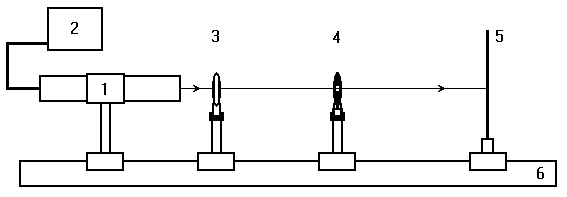
Рис. 4. Схема лабораторной установки
2.2. Получение увеличенного изображения интерференционной картины
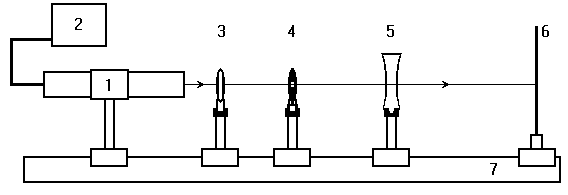
Рис. 5. Схема лабораторной установки
Лабораторная установка (рис.5) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), короткофокусной собирающей линзы (3) с фокусным расстоянием f1= 1 см, бипризмы Френеля (4), рассеивающей линзы (5) с фокусным расстоянием f2= -11 см, и экрана (6). Все элементы установлены на оптической скамье (7).
Линзы закреплены в оправах и устанавливаются в рейтеры, которые могут перемещаться вдоль оптической скамьи. Положение всех элементов на скамье определяется с помощью шкалы, прикрепленной к оптической скамье, или линейки. Все оптические детали центрируются, т.е. должны быть установлены так, чтобы их центры лежали на одной высоте, оптические оси линз были параллельны ребру оптической скамьи, плоскость экрана была перпендикулярна оптической оси линз.
3. Порядок выполнения работы
3.1. Установить оптические элементы согласно рис.4. Включить лазер.
3.2. Съюстировать линзу (3) по лучу лазера. Луч должен проходить вдоль главной оптической оси линзы. Это можно проконтролировать по отражению от поверхности линзы: отраженный луч должен попадать в выходное отверстие лазера. При этом лазерный пучок собирается в точку в фокальной плоскости.
3.3. Установить бипризму на расстоянии a
8–10 см от точки фокуса линзы. Расположить ее так, чтобы ребро бипризмы находилось в середине расфокусированного пятна.
3.4. Установить экран на расстоянии b
100 см от бипризмы. На экране будет наблюдаться интерференционная картина, образованная двумя когерентными пучками, идущими от мнимых источников, расстояние l между которыми вычисляется по формуле:
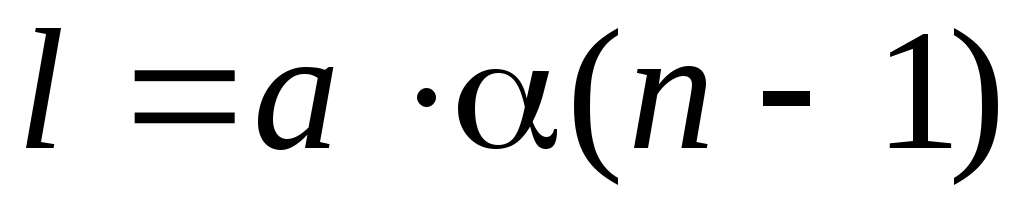 , (12)
, (12)
где a - угол между преломляющей гранью и основанием бипризмы (a = 20/ = 5,8.10-3 рад).
-
Измерить ширину интерференционной полосы Dy (расстояния между соседними максимумами) не менее трёх раз. С целью увеличения точности измерения Dy нужно определять расстояние между максимально удаленными друг от другаi-й и k-й интерференционными полосами и делить его на 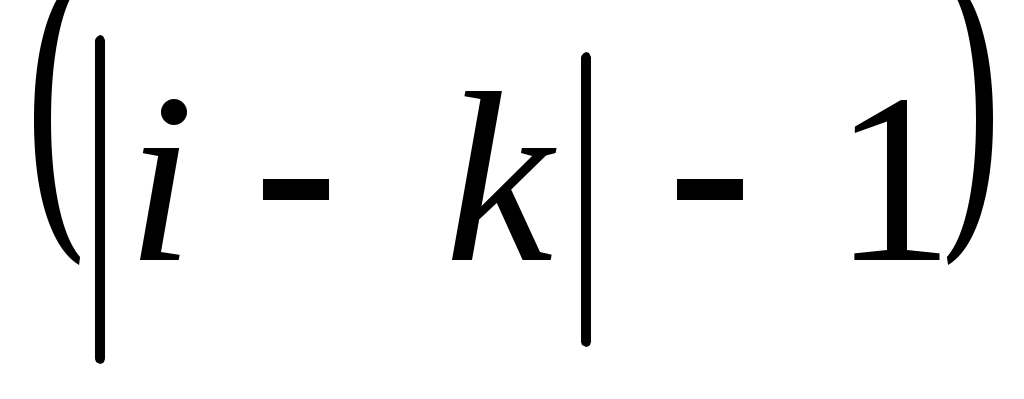 .
.
-
По формуле:
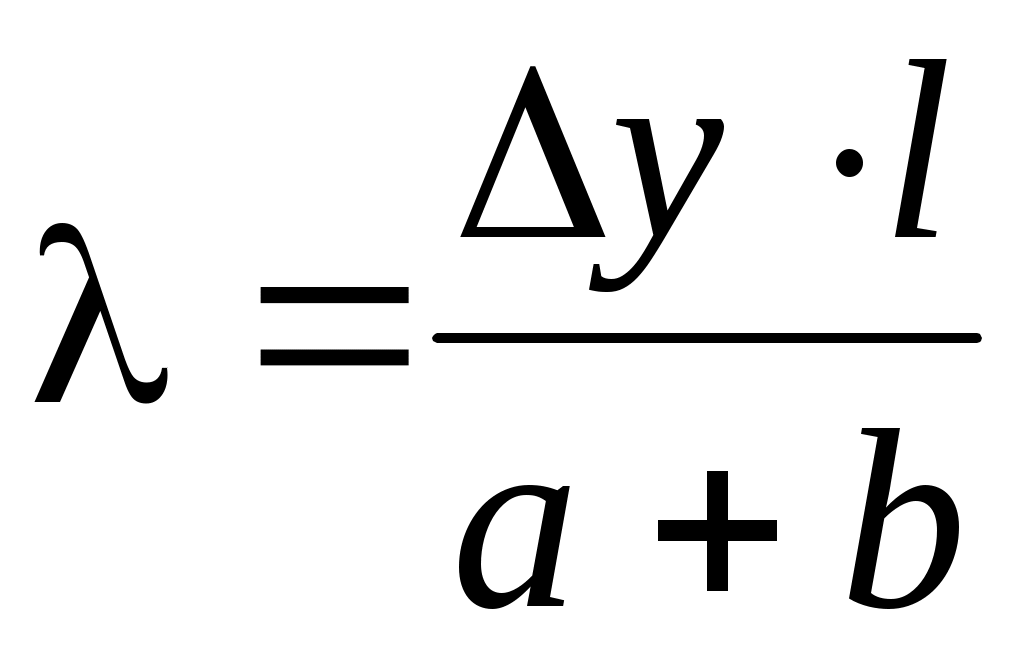 (13)
(13)
определить длину волны l излучения лазера для различных значений Dy.
3.7. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.8. Установить оптические элементы согласно рис.5. Получить увеличенную интерференционную картину. Ширина интерференционной полосы при наличии рассеивающей линзы будет определяться выражением:
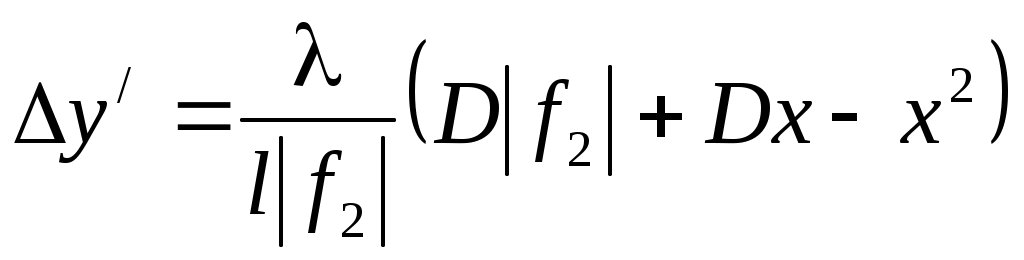 , (14)
, (14)
где x - расстояние между мнимыми источниками и рассеивающей линзой, D - расстояние между экраном и мнимыми источниками. Измерить Dy’ при разных положениях линзы не менее трёх раз.
3.9. Определить из формулы (14) длину волны лазера для различных значений Dy’. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.10. Сравнить полученный результат с истинной длиной волны лазера и со значением, полученным в п.3.7.
4. Контрольные вопросы и задания
-
В чем состоит классический опыт Юнга по наблюдению интерференционной картины? Из какого условия находятся минимальные и максимальные значения интенсивности на экране для этого случая?
-
Что называется интерференцией?
-
В результате интерференции каких волн получается четкая интерференционная картина?
-
Как связаны между собой когерентность и монохроматичность световых волн?
-
Может ли наблюдаться интерференционная картина в солнечном свете?
-
Какие существуют способы получения когерентных волн в оптике?
-
Объясните принцип действия билинзы Бийе, бизеркал Френеля, зеркала Ллойда?
-
Точечный монохроматический источник света (l = 0,5 мкм) расположен на оси симметрии бипризмы Френеля, перпендикулярной наибольшей стороне, на расстоянии 0,1 м от бипризмы, а плоский экран находится на расстоянии 2,9 м от бипризмы. Сколько белых и темных полос образуется на экране (угол a при вершине бипризмы составляет 20’, толщиной бипризмы в расчетах можно пренебречь)?
-
Найдите распределение интенсивности на экране в установке с зеркалами Френеля. Интерферирующие лучи падают на экран приблизительно перпендикулярно его поверхности.
-
Найдите ширину полос интерференции в установке с зеркалом Ллойда, если известна длина волны излучения, расстояние от вторичных источников до экрана и расстояние от источника до зеркала.
Лабораторная работа
КОЛЬЦА НЬЮТОНА
ЦЕЛЬ РАБОТЫ: изучение явления интерференции в тонких клиньях с помощью колец Ньютона (полосы равной толщины), определение радиуса кривизны линзы и длины световой волны с помощью такой интерференционной схемы.
ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, ртутная лампа, оптическая скамья, набор светофильтров, микроскоп, волоконный световод, система «линза-пластинка» для наблюдения колец Ньютона.
1. Теоретическая часть [1¸6]
1.1. Виды интерференционных полос
Происхождение интерференционной картины и способ ее получения определяют вид интерференционных полос, представляющих собой чередующиеся максимумы и минимумы интенсивности света.
Пусть интерференционное устройство представляет собой слой прозрачного диэлектрика с частично отражающими и пропускающими поверхностями, в котором возникает геометрическая разность хода D при произвольном угле падения j света на это устройство. К такому типу интерферометров можно отнести плоскопараллельные и клиновидные диэлектрические пластины (например, интерференция в тонких пленках, кольца Ньютона и др.), а также интерферометры, расщепляющие пучки с помощью зеркал (интерферометр Майкельсона и его аналоги, эталон Фабри-Перо). Здесь можно рассмотреть три вида интерференционных полос, получающихся при следующих условиях:
-
l = const; j = const. При вариации геометрической разности хода имеют место полосы равной толщины.
-
l = const; D = const. При вариации угла падения получаем полосы равного наклона.
-
j = const; D = const. При вариации длины волны получаем полосы равного хроматического порядка.
Полосы равной толщины возникают в том случае, если интерферирующие пучки после прохождения интерференционной системы имеют реальное или мнимое пересечение в пространстве изображений.
Полосы равного наклона возникают между параллельными пучками света, которые после прохождения интерферометра приобретают определенную разность хода.
Полосы равного хроматического порядка в интерференционных схемах используется крайне редко (для очень точных измерений толщины плоскопараллельных пластин или воздушных промежутков).
1.2. Интерференция в тонких пленках
При распространении световой волны в среде уменьшается скорость распространения волны и соответственно ее длина, т.к. частота не изменяется. При расчете изменения фаз волны в среде в качестве длины пути удобнее брать оптическую длину пути, равную геометрической длине, умноженной на показатель преломления:
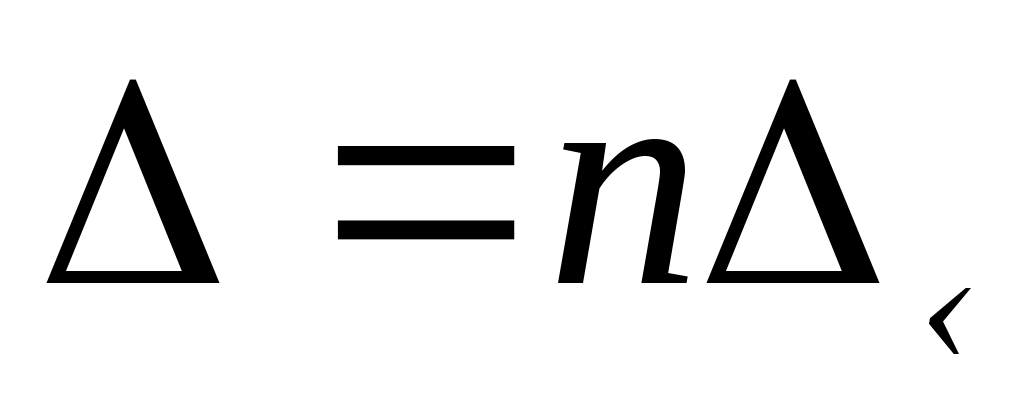 . (1)
. (1)
Тогда длину волны и волновой вектор в формулах можно задавать равными их значениям в вакууме. Аналогично (1) вводится и связь между геометрической и оптической разностью хода.
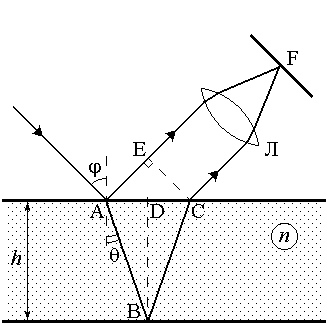
Рис.1
Полосы равного наклона. Рассмотрим случай, когда плоская монохроматическая волна падает под углом j на поверхность плоскопараллельной пластинки с относительным показателем преломления n и толщиной h(рис.1). Интерференция возникает между двумя волнами, отраженными от верхней и нижней поверхностями пластины. Так как эти пучки параллельны между собой, то интерференция наблюдается (локализована) или на бесконечности, или в фокальной плоскости Fлинзы Л. С учетом потери полволны на границе раздела сред (если n> 1, то в точке A, если n< 1, то в точке B) оптическая разность хода в данном случае равна
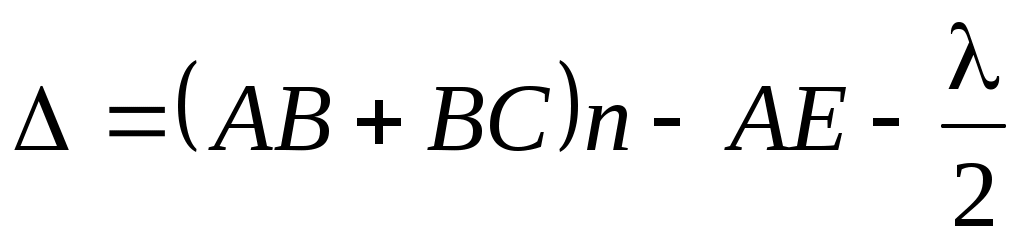 . (1)
. (1)
Проведем ряд несложных преобразований для нахождения оптической разности хода.
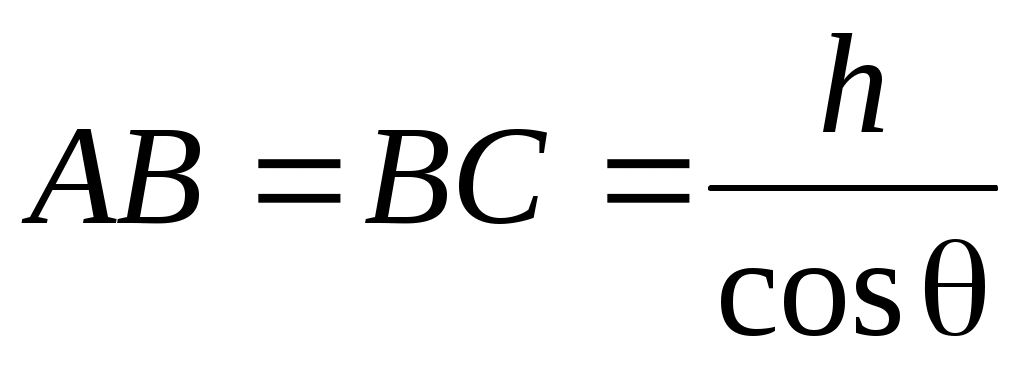 . (2)
. (2)
Тогда
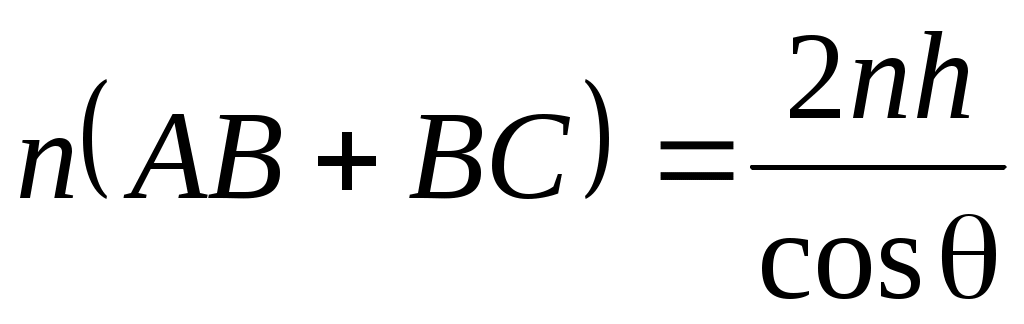 . (3)
. (3)
Далее,
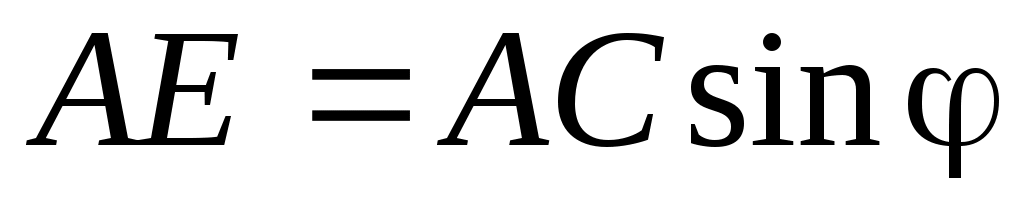 . (4)
. (4)
Но
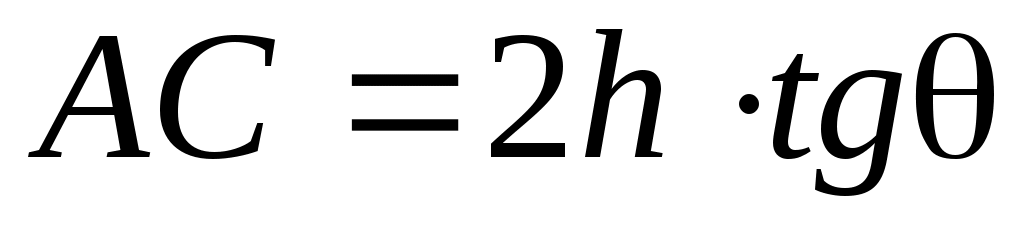 . (5)
. (5)
Поэтому
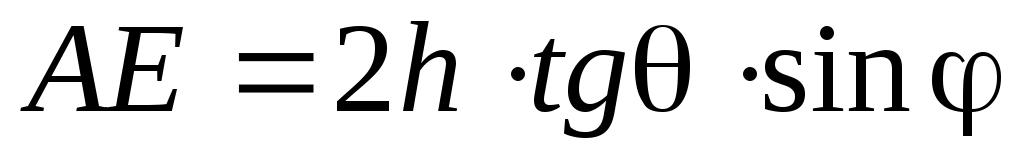 . (6)
. (6)
Тогда:
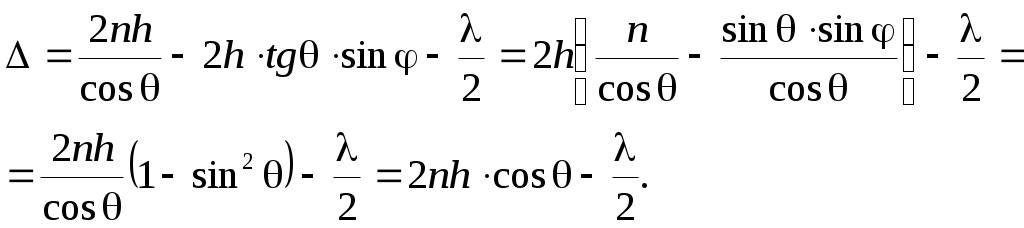 (7)
(7)
Здесь учтена связь из закона Снеллиуса углов падения j и преломления q:
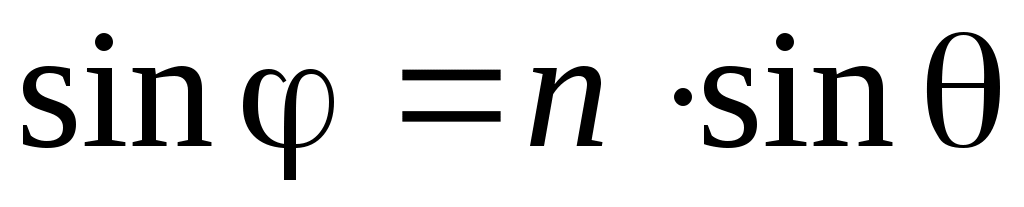 . (8)
. (8)
Таким образом, получаем для оптической разности хода:
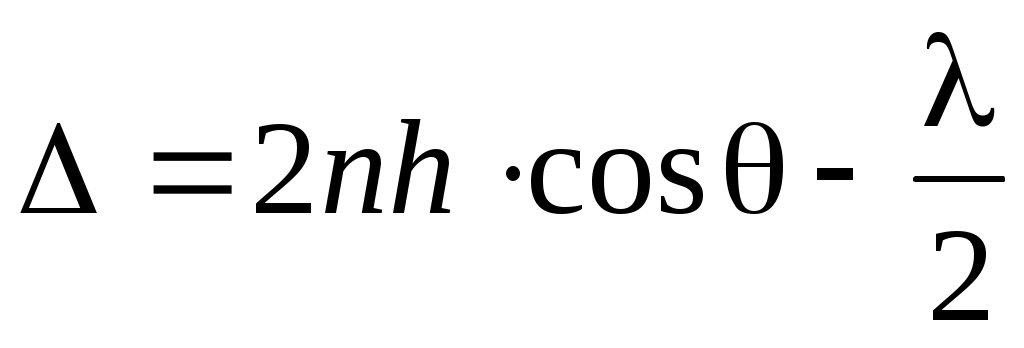 . (9)
. (9)
Условием максимума интерференционной картины является (см. лабораторную работу «Бипризма Френеля»:
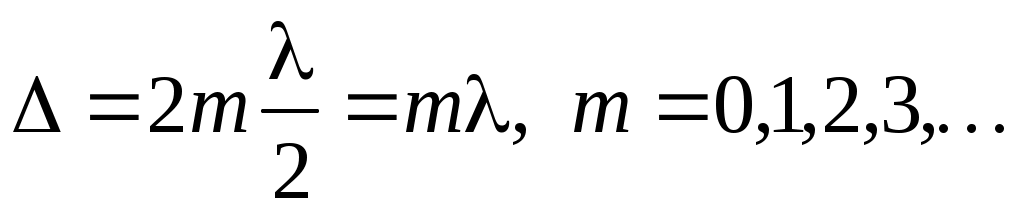 . (10)
. (10)
а условием минимума –
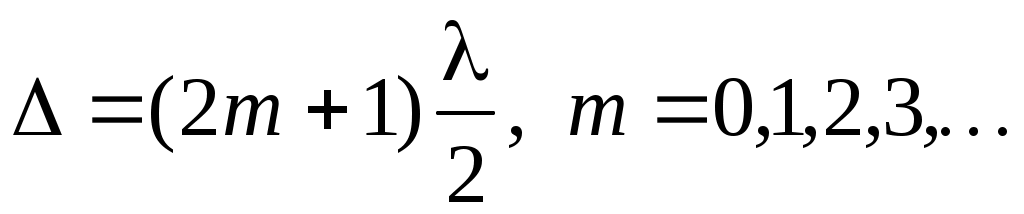 (11)
(11)
Если на пластинку падают непараллельные пучки света, то и интерферирующие пучки будут иметь все всевозможные направления распространения. При заданных толщине пластины и показателе преломления каждому углу падения волны соответствует своя интерференционная полоса. Поэтому такие полосы и называют полосами равного наклона. При аксиально симметричном распределении падающих пучков линии равного наклона являются окружностями.
Даже если источник света протяженный, и различные его точки излучают некогерентно, интерференционные картины не зависят от фазы волны в точке расщепления пучков на поверхности пластины (точка A на рис.1) и от положения этой точки, а зависят лишь от угла падения. Поэтому конечность размеров источника не смазывает картину полос равного наклона и не является ограничивающим интерференцию фактором.
Если падающий свет не монохроматичный, при увеличении разности длин падающих волн интерференционные кольца разделяются и при некотором значении этой разности полосы соседних порядков перекрываются. Разность длин волн, при которой наступает перекрытие полос соседних порядков интерференции, называется дисперсионной областью(или областью свободной дисперсии). Увеличение толщины пластины уменьшает дисперсионную область. Для наблюдения интерференции в белом свете толщина должна быть достаточно малой (
10 мкм). Поэтому в данном случае речь идет об интерференции в тонких пленках.
ИНТЕРФЕРЕНЦИЯ СВЕТА
Лабораторная работа
ИНТЕРФЕРЕНЦИЯ СФЕРИЧЕСКИХ ВОЛН
(БИПРИЗМА ФРЕНЕЛЯ)
ЦЕЛЬ РАБОТЫ: изучение явления двухлучевой интерференции с помощью бипризмы Френеля, определение длины световой волны с использование данной интерферометрической схемы.
ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, две линзы (собирающая и рассеивающая), бипризма Френеля, экран, линейка, оптическая скамья с набором рейтеров.
1. Теоретическая часть [1¸6]
1.1. Интерференция волн
В эксперименте возможна ситуация, когда интенсивность света, создаваемая какими-либо двумя источниками, не равна сумме интенсивностей отдельных источников. Оказывается, что если свет от одного источника разделить прибором на два пучка и заставить их проходить разные пути, а затем наложить их друг на друга, то интенсивность их в области суперпозиции пучков будет изменяться от точки к точке. Она может достигать максимума, превышающего сумму интенсивностей пучков, и минимума, который может оказаться равным нулю. Это явление называется интерференцией. Оказывается, что при суперпозиции пучков строго монохроматического света интерференция возникает всегда. Однако, свет от физических источников никогда не бывает строго монохроматическим. Как следует из теории излучения атома, его амплитуда и фаза флуктуируют непрерывно и так быстро, что ни глаз, ни быстрый физический детектор не могут уследить за их изменениями.
Если две световых волны происходят от одного источника, то возникающие в них флуктуации амплитуды и фазы, вообще говоря, коррелированы, и о таких волнах говорят, что они полностью или частично когерентны, в зависимости от того, будет ли эта корреляция полной или частичной. В общем случае колебания (или волны) называются когерентными, если разность их фаз остается постоянной (или изменяется по определенному закону) во времени. В световых пучках от разных источников флуктуации совершенно независимы и пучки, как говорят, взаимно некогерентны. При наложении таких пучков от независимых источников интерференция в обычных экспериментальных условиях не наблюдается. Детальный анализ показывает, что «степень корреляции» между флуктуациями в двух световых пучках определяет «четкость» интерференционных эффектов, возникающих при суперпозиции пучков и, наоборот, «степень корреляции» сама определяется этими эффектами.

Рис.1
Рассмотрим вначале классическую схему Юнга наблюдения интерференционной картины для простейшего случая двух гармонических волн. Пусть два точечных источника S1 и S2 , расположенных на расстоянии 2l друг от друга излучают две монохроматические сферические когерентные волны 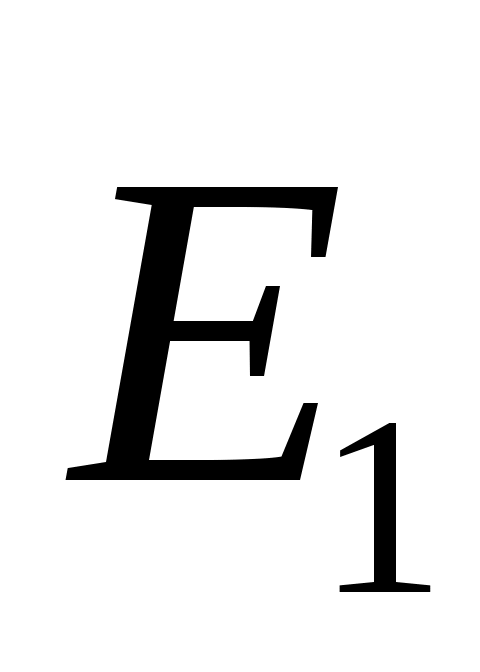 и
и 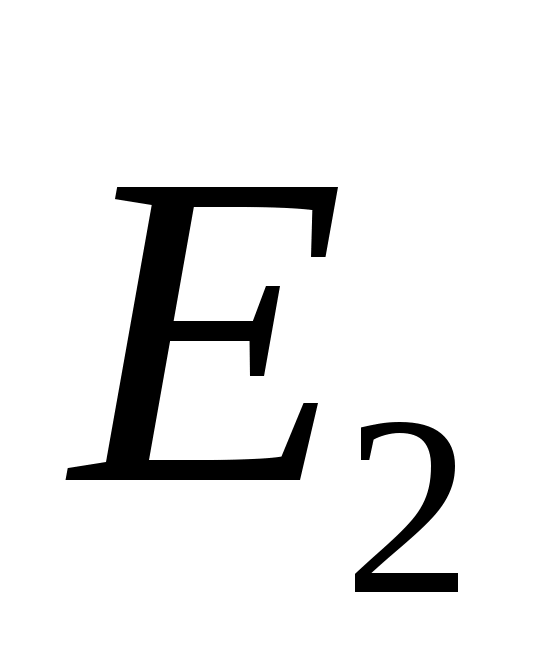 (рис.1). Предположим, что расстояние D от источников до экрана значительно больше 2l и положим для простоты, что амплитуды волн E1и E2в точке Р одинаковы и равны Е0 . Найдем результирующую амплитуду волн в точке Р, если
(рис.1). Предположим, что расстояние D от источников до экрана значительно больше 2l и положим для простоты, что амплитуды волн E1и E2в точке Р одинаковы и равны Е0 . Найдем результирующую амплитуду волн в точке Р, если
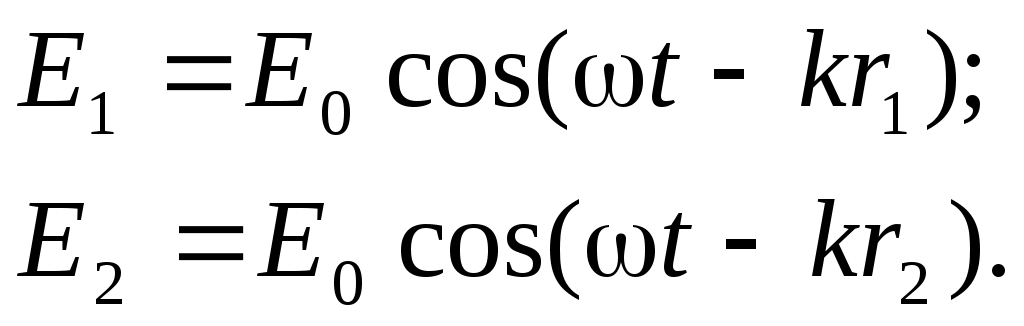 (1)
(1)
Тогда суммарная волна в точке Р:
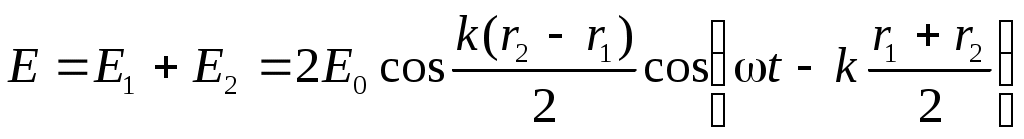 . (2)
. (2)
Введем величину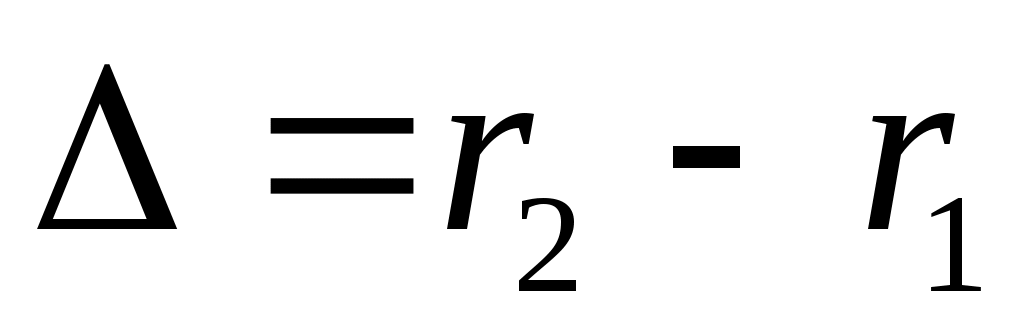 , называемую геометрической разностьюхода. Тогда интенсивность света будет равна:
, называемую геометрической разностьюхода. Тогда интенсивность света будет равна:
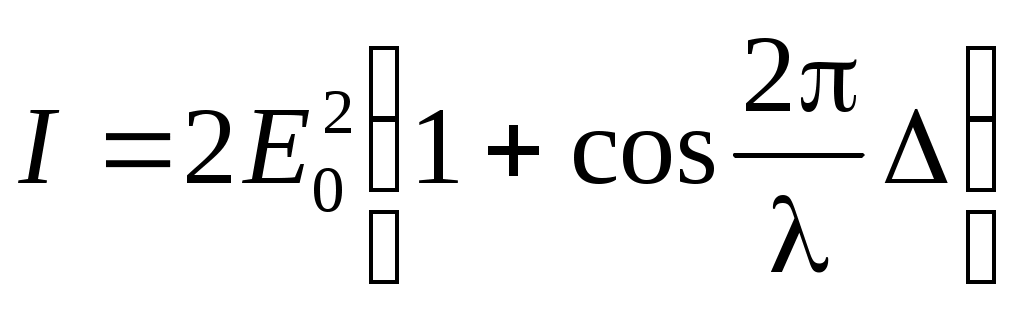 . (3)
. (3)
Видим, что
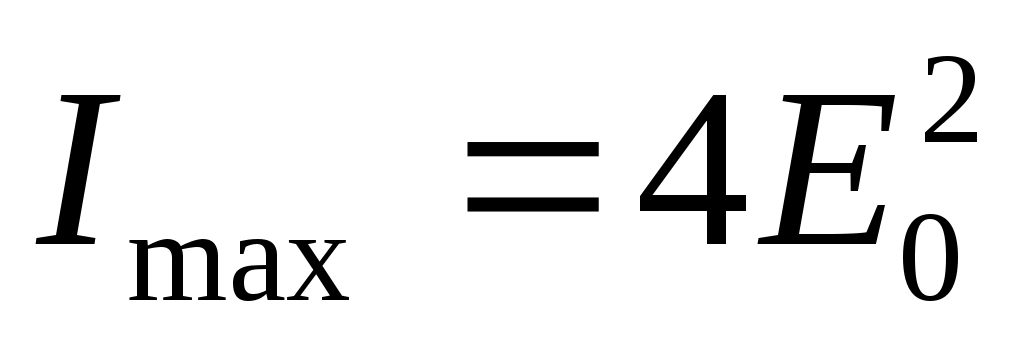 при
при 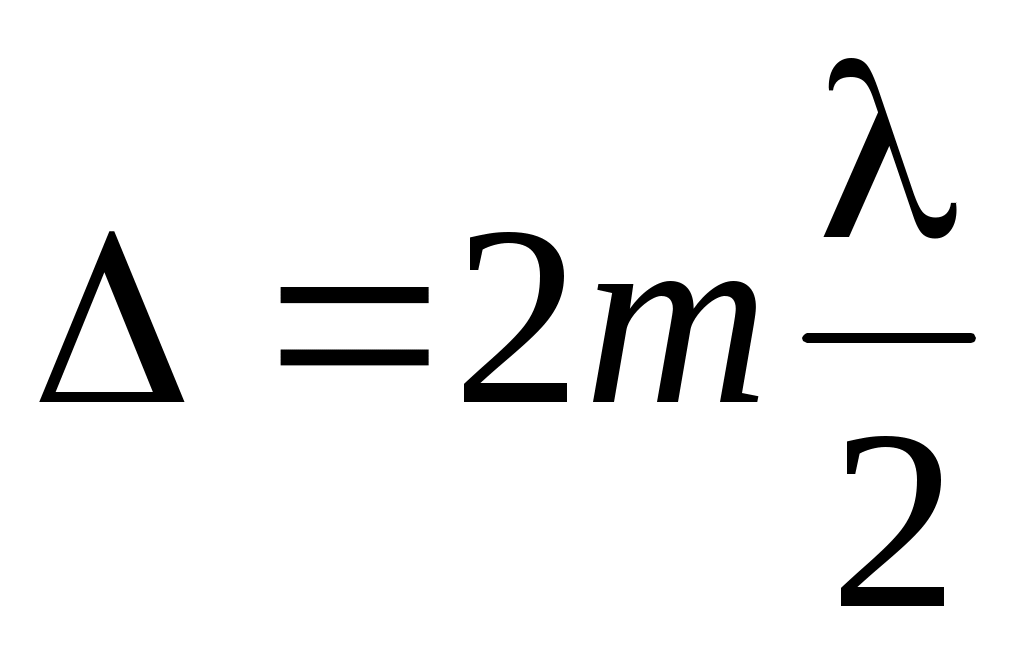 ; (4)
; (4)
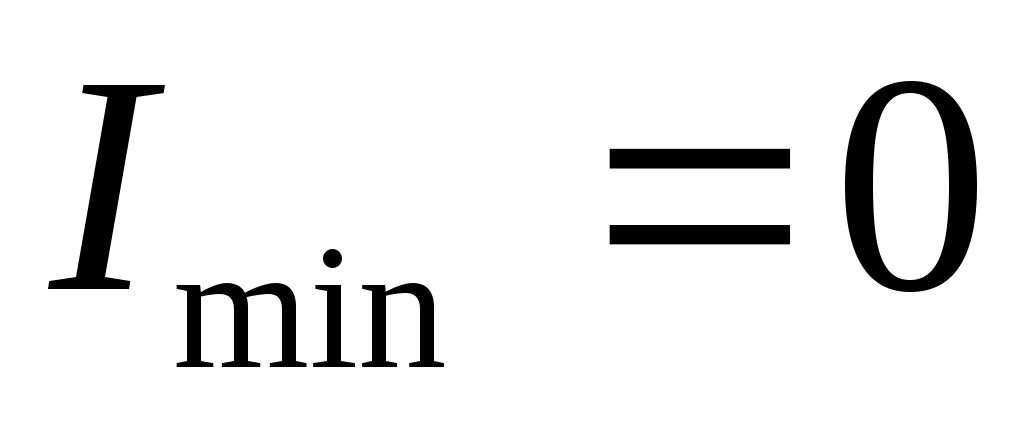 при
при 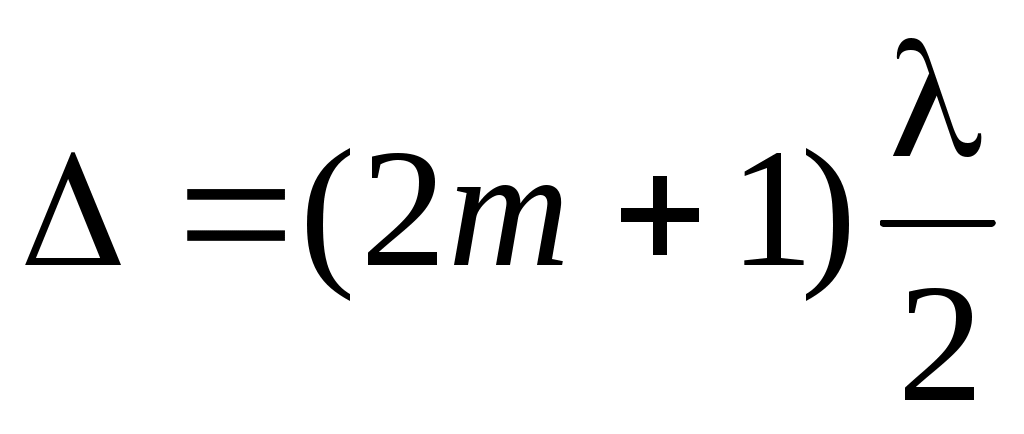 . (5)
. (5)
Таким образом, в результате наложения двух когерентных волн мы будем наблюдать в пространстве (или на экране, как это делается в эксперименте) чередующуюся в зависимости от разности хода картину максимумов и минимумов, называемую интерференционными полосами.
1.2. Получение когерентных световых волн с помощью бипризмы Френеля
Для получения когерентных световых волн от реальных источников пользуются следующим искусственным приемом. Волновой фронт разделяют на несколько частей. Полученные таким образом волны проходят различные оптические пути и при дальнейшем сложении уже обладают разностью хода, оставаясь когерентными. Потому, что разность хода зависит только от конструкции прибора.

Рис.2
На рис. 2 приведен способ деления фронта волны на две части с помощью бипризмы Френеля. Важно отметить, что в практических приборах разность хода не делается обычно больше 100 ¸ 200 мм, т.к. длительность излучения атома
10-8 с, и при большой разности хода может случиться, что будут складываться волны, полученные уже от разных актов испускания, т.е. когерентность нарушится. Бипризма Френеля имеет малые преломляющие углы (a = 30/ ) и разность хода, приобретаемая волнами здесь мала. После преломления в бипризме падающий пучок света разделяется на два когерентных пучка с источниками в мнимых изображениях S‘ и S“ источника S (рис.3). Вычислим разность хода волн, приходящих в точку Р, через геометрические размеры оптической схемы.
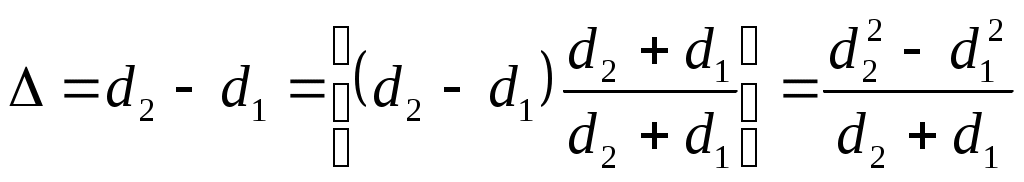 . (6)
. (6)
Считая, что в практических схемах d » D, ОР = y«D и следовательно: 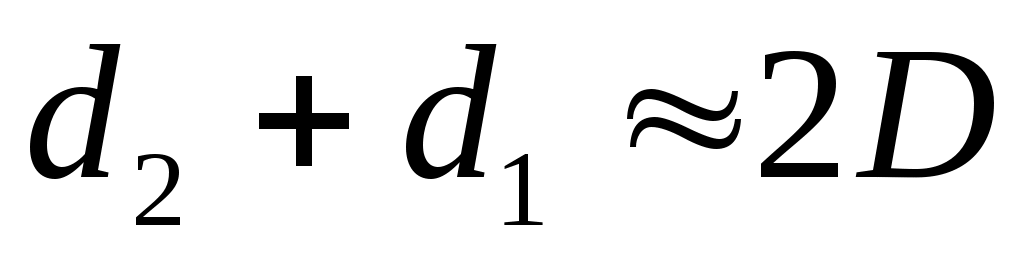 , получим:
, получим:

Рис.3
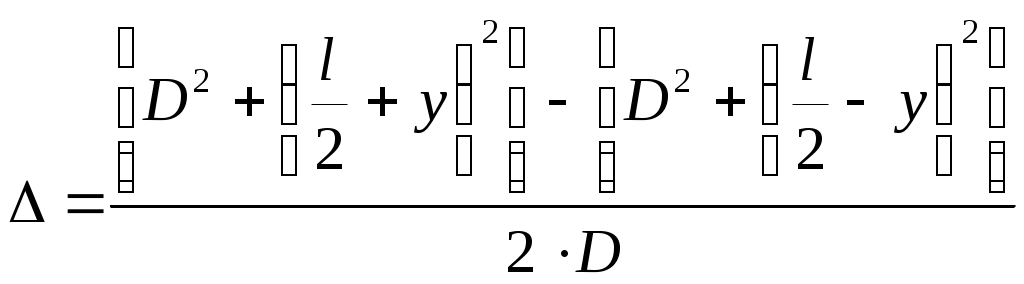 (7)
(7)
Преобразуя (7), получим:
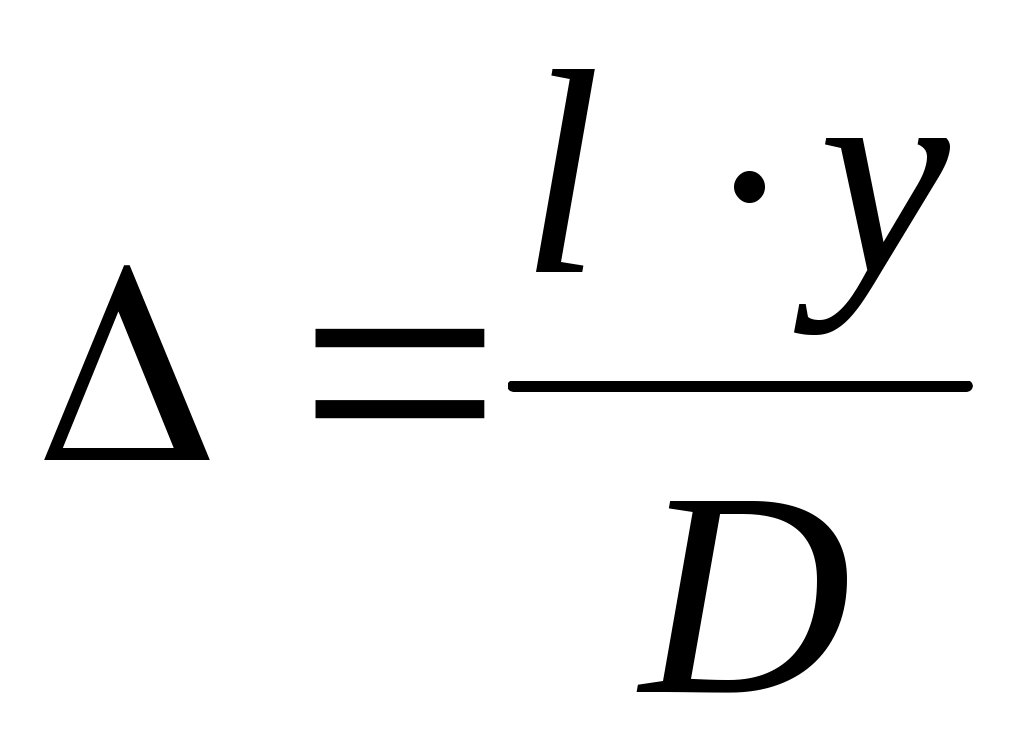 (8)
(8)
Пользуясь условием (4), при котором получается максимум интенсивности на экране, находим:
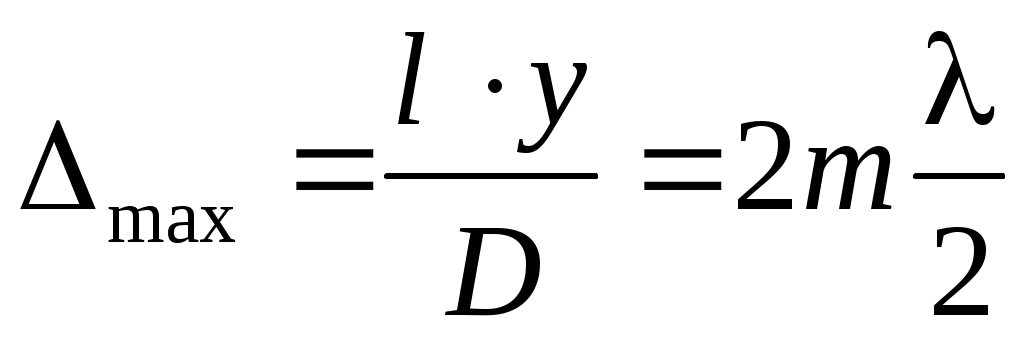 ; (9)
; (9)
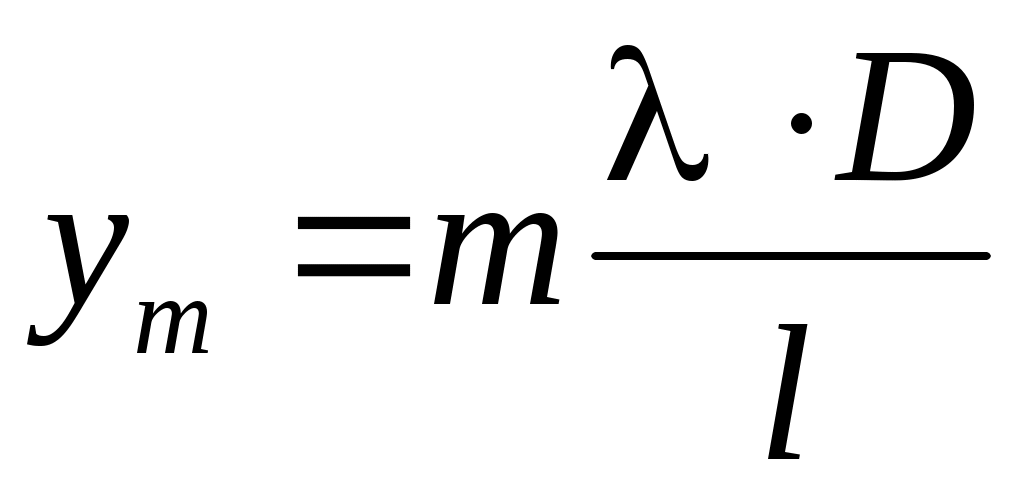 . (10)
. (10)
Соотношение (10) показывает, что максимумы отстоят друг от друга на равных расстояниях. Обозначая расстояние, соответствующее одному из максимумов ym, а следующему ym+1, получим:
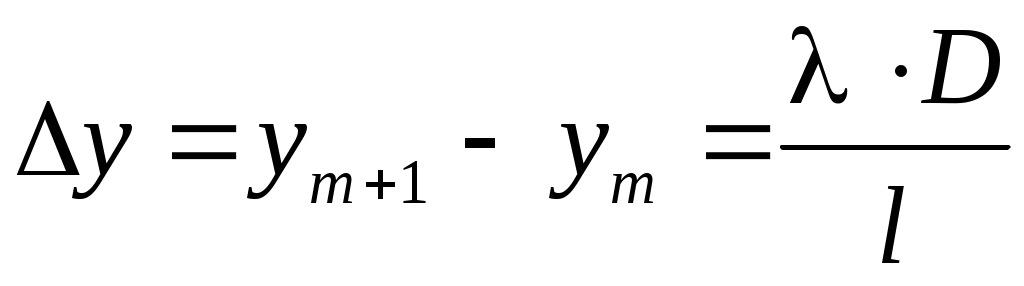 . (11)
. (11)
2. Описание установки
2.1. Определение длины световой волны с помощью бипризмы Френеля
Лабораторная установка (рис.4) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), короткофокусной собирающей линзы с фокусным расстоянием f1= 1 см (3), бипризмы Френеля (4) и экрана (5). Все элементы установлены на оптической скамье (6).

Рис. 4. Схема лабораторной установки
2.2. Получение увеличенного изображения интерференционной картины

Рис. 5. Схема лабораторной установки
Лабораторная установка (рис.5) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), короткофокусной собирающей линзы (3) с фокусным расстоянием f1= 1 см, бипризмы Френеля (4), рассеивающей линзы (5) с фокусным расстоянием f2= -11 см, и экрана (6). Все элементы установлены на оптической скамье (7).
Линзы закреплены в оправах и устанавливаются в рейтеры, которые могут перемещаться вдоль оптической скамьи. Положение всех элементов на скамье определяется с помощью шкалы, прикрепленной к оптической скамье, или линейки. Все оптические детали центрируются, т.е. должны быть установлены так, чтобы их центры лежали на одной высоте, оптические оси линз были параллельны ребру оптической скамьи, плоскость экрана была перпендикулярна оптической оси линз.
3. Порядок выполнения работы
3.1. Установить оптические элементы согласно рис.4. Включить лазер.
3.2. Съюстировать линзу (3) по лучу лазера. Луч должен проходить вдоль главной оптической оси линзы. Это можно проконтролировать по отражению от поверхности линзы: отраженный луч должен попадать в выходное отверстие лазера. При этом лазерный пучок собирается в точку в фокальной плоскости.
3.3. Установить бипризму на расстоянии a
8–10 см от точки фокуса линзы. Расположить ее так, чтобы ребро бипризмы находилось в середине расфокусированного пятна.ИНТЕРФЕРЕНЦИЯ СВЕТА
Лабораторная работа
ИНТЕРФЕРЕНЦИЯ СФЕРИЧЕСКИХ ВОЛН
(БИПРИЗМА ФРЕНЕЛЯ)
ЦЕЛЬ РАБОТЫ: изучение явления двухлучевой интерференции с помощью бипризмы Френеля, определение длины световой волны с использование данной интерферометрической схемы.
ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, две линзы (собирающая и рассеивающая), бипризма Френеля, экран, линейка, оптическая скамья с набором рейтеров.
1. Теоретическая часть [1¸6]
1.1. Интерференция волн
В эксперименте возможна ситуация, когда интенсивность света, создаваемая какими-либо двумя источниками, не равна сумме интенсивностей отдельных источников. Оказывается, что если свет от одного источника разделить прибором на два пучка и заставить их проходить разные пути, а затем наложить их друг на друга, то интенсивность их в области суперпозиции пучков будет изменяться от точки к точке. Она может достигать максимума, превышающего сумму интенсивностей пучков, и минимума, который может оказаться равным нулю. Это явление называется интерференцией. Оказывается, что при суперпозиции пучков строго монохроматического света интерференция возникает всегда. Однако, свет от физических источников никогда не бывает строго монохроматическим. Как следует из теории излучения атома, его амплитуда и фаза флуктуируют непрерывно и так быстро, что ни глаз, ни быстрый физический детектор не могут уследить за их изменениями.
Если две световых волны происходят от одного источника, то возникающие в них флуктуации амплитуды и фазы, вообще говоря, коррелированы, и о таких волнах говорят, что они полностью или частично когерентны, в зависимости от того, будет ли эта корреляция полной или частичной. В общем случае колебания (или волны) называются когерентными, если разность их фаз остается постоянной (или изменяется по определенному закону) во времени. В световых пучках от разных источников флуктуации совершенно независимы и пучки, как говорят, взаимно некогерентны. При наложении таких пучков от независимых источников интерференция в обычных экспериментальных условиях не наблюдается. Детальный анализ показывает, что «степень корреляции» между флуктуациями в двух световых пучках определяет «четкость» интерференционных эффектов, возникающих при суперпозиции пучков и, наоборот, «степень корреляции» сама определяется этими эффектами.

Рис.1
Рассмотрим вначале классическую схему Юнга наблюдения интерференционной картины для простейшего случая двух гармонических волн. Пусть два точечных источника S1 и S2 , расположенных на расстоянии 2l друг от друга излучают две монохроматические сферические когерентные волны
Тогда суммарная волна в точке Р:
Введем величину
Видим, что
Таким образом, в результате наложения двух когерентных волн мы будем наблюдать в пространстве (или на экране, как это делается в эксперименте) чередующуюся в зависимости от разности хода картину максимумов и минимумов, называемую интерференционными полосами.
1.2. Получение когерентных световых волн с помощью бипризмы Френеля
Для получения когерентных световых волн от реальных источников пользуются следующим искусственным приемом. Волновой фронт разделяют на несколько частей. Полученные таким образом волны проходят различные оптические пути и при дальнейшем сложении уже обладают разностью хода, оставаясь когерентными. Потому, что разность хода зависит только от конструкции прибора.

Рис.2
На рис. 2 приведен способ деления фронта волны на две части с помощью бипризмы Френеля. Важно отметить, что в практических приборах разность хода не делается обычно больше 100 ¸ 200 мм, т.к. длительность излучения атома
3.4. Установить экран на расстоянии b
Измерить ширину интерференционной полосы Dy (расстояния между соседними максимумами) не менее трёх раз. С целью увеличения точности измерения Dy нужно определять расстояние между максимально удаленными друг от другаi-й и k-й интерференционными полосами и делить его на
По формуле:
В чем состоит классический опыт Юнга по наблюдению интерференционной картины? Из какого условия находятся минимальные и максимальные значения интенсивности на экране для этого случая?
Что называется интерференцией?
В результате интерференции каких волн получается четкая интерференционная картина?
Как связаны между собой когерентность и монохроматичность световых волн?
Может ли наблюдаться интерференционная картина в солнечном свете?
Какие существуют способы получения когерентных волн в оптике?
Объясните принцип действия билинзы Бийе, бизеркал Френеля, зеркала Ллойда?
Точечный монохроматический источник света (l = 0,5 мкм) расположен на оси симметрии бипризмы Френеля, перпендикулярной наибольшей стороне, на расстоянии 0,1 м от бипризмы, а плоский экран находится на расстоянии 2,9 м от бипризмы. Сколько белых и темных полос образуется на экране (угол a при вершине бипризмы составляет 20’, толщиной бипризмы в расчетах можно пренебречь)?
Найдите распределение интенсивности на экране в установке с зеркалами Френеля. Интерферирующие лучи падают на экран приблизительно перпендикулярно его поверхности.
Найдите ширину полос интерференции в установке с зеркалом Ллойда, если известна длина волны излучения, расстояние от вторичных источников до экрана и расстояние от источника до зеркала.
l = const; j = const. При вариации геометрической разности хода имеют место полосы равной толщины.
l = const; D = const. При вариации угла падения получаем полосы равного наклона.
j = const; D = const. При вариации длины волны получаем полосы равного хроматического порядка.