Файл: Дайте определение основным понятиям и терминам моделирования хим тех процессов. (модель хтп, хтс, моделирование, классификации моделей, традукция мат модели ).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 79
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Дайте определение основным понятиям и терминам моделирования хим.-тех. процессов. (модель ХТП, ХТС, моделирование, классификации моделей, традукция мат. модели ).
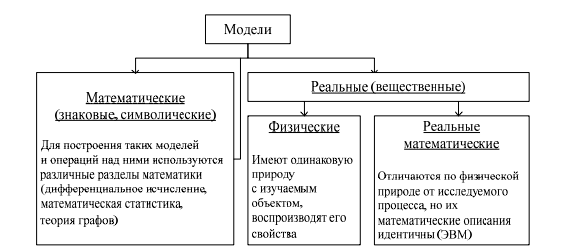
Математическим моделированием называют изучение свойств объекта на математической модели, целью которого является определение оптимальных условий протекания процесса, управление им на основе математической модели и перенос результатов на объект.
Математическая модель химико-технологического процесса (ХТП) – совокупность математических структур: формул, уравнений, неравенств и т. д., адекватно описывающая исследуемые свойства объекта. Реализованная на компьютере математическая модель называется компьютерной математической моделью, а проведение целенаправленных расчетов с помощью компьютерной модели называется вычислительным экспериментом.
Математическое моделирование включает в себя три взаимосвязанных этапа:
составление математического описания изучаемого объекта. Применительно к химической технологии математическая модель – совокупность математических зависимостей, отражающих в явной форме сущность химико-технологического процесса и связывающих его физические, режимные, физико-химические и конструктивные параметры;
выбор метода решения системы уравнений математического описания и реализация его в форме моделирующей программы;
установление соответствия (адекватности модели объекту).
Традуктивность (от лат. traductio – перенесение, перевод) предполагает возможность количественного перенесения результатов моделирования на реальный объект. Традуктивность моделирования тесно связана с условием подобия между моделью и оригиналом. С учетом теории подобия можно сформулировать правило традукции: безразмерные комплексы (критерии подобия) в сходственных точках подобных объектов (то есть модели и оригинала) равны.
В общем случае под моделью понимают мысленно представляемую или материально реализованную систему, которая отображает и (или) воспроизводит реальный объект исследования (и, соответственно, позволяет получать о нем новые сведения).
-
Оптимизация модели химико-технологического процесса. (постановка задачи оптимизации, критерий оптимальности, функция цели, ограничения, оптимизирующие параметры)
Оптимизация – процесс достижения наилучших или определение (нахождение) наиболее благоприятных условий проведения какого-либо процесса (действия). В приложении к технологическому процессу – определение наилучших условий проведения процесса.
При постановке задачи оптимизации необходимо иметь количественную оценку качества работы оптимизируемой системы, которая позволяет сравнивать различные состояния системы между собой. Эта количественная оценка носит название критерия оптимизации.
При постановке задачи оптимизации необходимо требовать достижения экстремального значения лишь одной величины. Таким образом, одновременно системе не должно приписываться два или более критериев оптимальности, поскольку практически во всех случаях экстремум одного критерия не соответствует экстремуму другого. Поэтому неправильная постановка задачи: получить максимальную производительность при минимальной себестоимости продукта; правильная постановка задачи: получить максимальную производительность при заданной себестоимости или получить минимальную себестоимость при заданной производительности. В первом случае критерий оптимальности – производительность, во втором – себестоимость.
Критерием оптимальности называется количественная оценка качества работы оптимизируемой системы. Критерий оптимальности – это главный признак, по которому судят о том, насколько хорошо функционирует технологическая система, работает данный процесс, и т.д., а также, насколько хорошо решена задача оптимизации. Критерий оптимальности является одним из выходных параметров системы, и, к нему предъявляются следующие требования:
1. критерий оптимальности должен выражаться количественно;
2. критерий оптимальности должен быть единственным;
3. величина критерия оптимальности должна изменяться монотонно (без разрывов и скачков);
4. критерий оптимальности должен отражать наиболее существенные стороны процесса;
5. желательно чтобы критерий оптимальности имел ясный физический смысл и легко рассчитывался.
На основании выбранного критерия оптимальности составляется целевая функция, представляющая собой зависимость критерия оптимальности от параметров, влияющих на ее значение.
Если в число оптимизирующих переменных включены конструктивные характеристики процесса (размеры, типы конструкций и т.п.), то решается задача оптимального проектирования.
Если в число оптимизирующих переменных не включены конструктивные характеристики процесса (размеры, типы конструкций и т.п.), то решается задача оптимального управления. В этом случае оптимизирующие переменные называются управляющими переменными и поиск их оптимальных значений осуществляется с целью определения наилучших режимных параметров действующих процессов.
-
Детерминированный и стохастический подходы к составлению математических моделей процесса, их возможность и сфера использования.
Детерминированный подход основан на применении детерминированной математической модели физической системы. При построении детерминированных моделей случайными факторами пренебрегают, учитывая лишь конкретные условия решаемой задачи, свойства и внутренние связи объекта (по этому принципу построены практически все разделы классической физики).
Детерминированная модель описывает процесс, в котором значение выходной величины однозначно определяется значением входной величины
Детерминированная модель допустима в следующих случаях:
-
влияние случайных факторов столь незначительно, что пренебрежение ими не приведет к ощутимому искажению результатов моделирования., -
детерминированная математическая модель отображает реальные физические процессы в усредненном смысле. В тех задачах, где не требуется высокой точности результатов моделирования, предпочтение отдается детерминированной модели. Это объясняется тем, что реализация и анализ детерминированной математической модели много проще, чем стохастической.
Детерминированная модель недопустима когда случайные процессы ω(t) соизмеримы с детерминированными x(t). Результаты, полученные с помощью детерминированной математической модели, будут неадекватными реальным процессам.
Стохастические (эмпирические, статистические) модели – отражают вероятностный характер явлений, когда рассчитывается не истинное значение параметров процесса, а вероятность их расчета в определенном интервале значений. Данные модели не несут информации о физикохимической сущности решаемой задачи, но их простота позволяет их эффективно использовать при моделировании химико-технологических процессов (ХТП). Стохастическая модель описывает процесс, в котором значение выходной величины не находится в однозначном соответствии с входной величиной.
Для анализа стохастических ММ необходимо использовать методы теории вероятностей, случайных процессов и математической статистики. Однако основная трудность их применения обычно связана с тем, что вероятностные характеристики случайных величин (математические ожидания, дисперсии, законы распределения) часто не известны или известны с невысокой точностью, т.е. ММ не удовлетворяет требованию продуктивности ММ. В таких случаях эффективнее использовать ММ, более грубую по сравнению со стохастической, но и более устойчивую по отношению к недостоверности исходных данных, т.е. в большей мере удовлетворяющую требованию робастности.
-
Материальные и мысленные модели. Физическое моделирование, область применения.
Материальное моделирование предполагает наличие связи, имеющей материальный характер, между моделью и исследуемым объектом. В материальном моделировании можно условно выделить три основные группы методов: пространственное, физическое и аналоговое моделирование. В пространственном моделировании используются модели, предназначенные для воспроизведения или отображения пространственных (геометрических) свойств изучаемых объектов. В качестве примеров такой группы моделей можно назвать макеты разнообразных типов (зданий, устройств и т.д.). В физическом моделировании используются модели, предназначенные для воспроизведения динамики процессов, происходящих в изучаемых объектах, причем общность процессов, происходящих в объекте исследования и модели, основывается на сходстве их физической природы. Наиболее известным примером физического моделирования является исследование летательных аппаратов на основе экспериментов в аэродинамической трубе. В аналоговом моделировании используются материальные модели, физическая природа которых отличается от природы исследуемых объектов, но, вместе с тем, они
описываются сходными математическими соотношениями, т.е. связь между моделью и объектом основывается на аналогии их математического описания.
Идеальное моделирование принципиально отличается от материального, поскольку оно основывается не на материальной аналогии между моделью и изучаемым объектом, а на идеальной, т.е. мыслимой связи между ними. В формализованном моделировании моделями служат системы знаков или образов, вместе с которыми задаются правила их преобразования и интерпретации. В знаковом (символьном) моделировании в качестве моделей используются системы знаков, которые могут существенно отличаться друг от. Важнейшим видом знакового моделирования является математическое моделирование, при использовании которого модель записывается в виде совокупности формул, преобразуемых на основе правил логики и математики. В образном моделировании при построении модели используются такие наглядные элементы, как упругие шары, потоки жидкости, траектории движения тел. Неформализованное моделирование – это анализ проблем разнообразного типа, когда модель не формулируется, а вместо нее используется некоторое, не зафиксированное точно, мысленное ощущение реальности, служащее основой для рассуждения и принятия решений
-
Математическое моделирование химического реактора идеального смешения. (основные формулы для расчетов)
Уравнение такой модели записывают в виде математического выражения, характеризующего изменение концентрации в реакционной среде во времени, которое обусловливается, во-первых, движением потока (гидродинамический фактор) и, во-вторых, химическим превращением (кинетический фактор). Поэтому указанную модель следует строить на основе типовой модели идеального перемешивания с учетом скорости химической реакции, т.е. записать изменение концентрации как алгебраическую сумму:
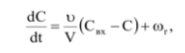
где ωr – скорость химической реакции.
Аналогичных уравнений записывают столько, сколько веществ участвует в реакции. Тогда переменная С будет концентрацией соответствующего i-го вещества (СA, CB, ...) и ωr – скоростью реакции по тому же i-му веществу. Система указанных уравнений будет математической моделью рассматриваемого реактора идеального перемешивания с учетом изменения Ci во времени (динамическая модель).