Если принять, что исходным является вещество А, и заменить величины

(вещество А убывает), а также представить время пребывания как отношение реакционного объема к объемной скорости τ=V/ 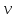то уравнение (1) примет вид:
(2)

При установившемся режиме работы реактора, который характеризуется соблюдением условия 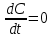, уравнение (2) можно записать так:


Уравнение (3) является статической моделью химического реактора идеального перемешивания в общем виде.

6. 
   Адекватность математической модели ХТП. Проверка на адекватность полученной модели.
   

Под адекватностью математической модели понимается соответствие ее реальному объекту как качественное (тенденции изменения переменных в модели и в объекте должны быть одинаковы), так и количественное (экспериментальные данные должны совпадать с расчетными).



Адекватная ММ ХТП подвергается исследованию, в ходе которого анализируется параметрическая чувствительность модели, т. е. определяется влияние различных переменных и коэффициентов, в том числе и физико-химических моделей, на выходные переменные процесса. В результате выявляются наиболее подходящие ресурсы для управления реальным процессом и его оптимизации. Одновременно ХТП моделируется (симулируется) на компьютере, т. е. проводятся его расчетные исследования с целью анализа поведения процесса при различных условиях и всевозможных режимах работы. Это позволяет с использованием адекватных компьютерных моделей определять «узкие места» химических производств и возможности их совершенствования и модернизации.

7. Математическое моделирование химического реактора идеального вытеснения. (основные формулы для расчетов)

Данную модель записывают в виде дифференциального уравнения, которое описывает распределение вещества в реакционной среде как за счет гидродинамических факторов, так и за счет химического превращения.

---

Следовательно, в общем виде такое математическое описание, построенное на основе типовой модели идеального вытеснения с учетом влияния скорости химической реакции, должно быть представлено алгебраической суммой:


Аналогичные уравнения записывают для всех участвующих в реакции веществ. В результате получим математическое описание процесса в реакторе вытеснения с учетом изменения переменной С (концентрация i-го вещества) во времени, т. е. динамическую модель.

Для установившегося режима работы реактора, когда 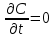, уравнение (5) описывает статику процесса химического превращения и после замены 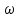_{r = 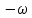rA} (исходное вещество А убывает) принимает такой вид:


Если учесть, что линейная скорость а элемент длины то

уравнение (6) примет вид:

Теловой режим в реакторе идеального вытеснения описывается уравнением:


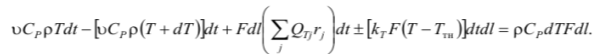
Уравнение теплового баланса для установившегося режима после преобразований

8. 
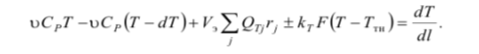
   Использование разложения в степенной ряд Тейлора для решения эмпирических уравнений.
   

9. Этапы построения математической модели ХТП. (описать последовательность, блок схема построения мат. модели, рассказать, что происходит на каждом этапе).

---

10. 
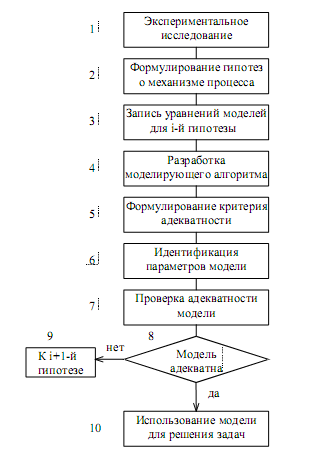
    Понятие о планировании эксперимента. Пассивные и активные эксперименты. Какими оптимальными свойствами должен обладать план эксперимента? (на лекциях не успели, есть в 5 лабораторной работе и учебнике)
    

Чтобы составить статистическую модель необходимо иметь достаточный объем статистического материала, получаемого в результате исследования. В зависимости от сбора статистического материала для построения статистической модели различают пассивный и активный (планируемый) эксперимент.

Пассивный эксперимент проводится в режиме нормальной эксплуатации объекта и предполагает регистрацию контролируемых параметров без внесения искусственных возмущений в его работу.

Преимущества пассивного эксперимента:

1) простота его организации и «невмешательство» в ход технологического процесса.

Недостатки:

1) ограниченность действия полученной математической модели областью рабочего режима процесса

2) в следствие сложности, протекающих химико-технологических процессов не всегда удается составить их математическую модель в рамках теоретических предпосылок статистических методов.

Активный (планируемый) эксперимент предполагает, что на вход исследуемого объекта подаются определенные воздействия, которые заранее планируются в соответствии с определенным оптимальным критерием (методы планирования экспериментов).

Такая постановка эксперимента позволяет соблюсти теоретические предпосылки статистических методов, резко сократить количество экспериментов и получить математическую модель с min возможной ошибкой. Однако планируемый эксперимент не всегда удобно проводить на действующих технологических объектах. Поэтому его широко используют при исследовании опытных и пилотных установок.

---

План эксперимента устанавливает численные значения факторов и условия проведения опытов.

Критерии оптимальности планов и способы организации активного эксперимента можно разделить на три группы.

К I-й группе относят критерии, связанные с точностью оценок коэффициентов регрессии.

Ортогональность позволяет оценивать все коэффициенты регрессии независимо друг от друга и упрощать или усложнять модели, исключая или добавляя новые коэффициенты без пересчета уже найденных. Ортогональность плана эксперимента обеспечивает минимальное число вычислений.

Д-оптимальность обеспечивает минимум обобщенной дисперсии всех оценок коэффициентов. При составлении планов, обеспечивающих минимум обобщенной дисперсии только части оценок коэффициентов, план называется усеченным Д-оптимальным.

А-оптимальность обеспечивает минимум средней дисперсии оценок коэффициентов.

Е-оптимальность не дает возможности некоторым оценкам коэффициентов иметь слишком большие дисперсии.

Ко II-ой группе относят критерии, которые определяют точность предсказания отклика с помощью построенной модели.

Ротатабельность планов обеспечивает одинаковую точность предсказания для точек, равно удаленных от центра плана по любому направлению.

G-оптимальные планы гарантируют отсутствие в области эксперимента точек, имеющих слишком низкую точность оценки отклика.

Q-оптимальные планы минимизируют среднюю дисперсию предсказания.

К III-ей группе относят критерии, связанные со стратегией эксперимента.

Насыщенность плана обеспечивает минимум числа опытов. Минимум задается числом коэффициентов модели. Приближение к нему служит мерой насыщенности плана.

10. 
    Основные требования, предъявляемые к процессу моделирования. Теория подобия объекта и модели.
    

1. Модель должна строиться исходя из цели исследования системы (явления, процесса) и соответствия цели точности результатов моделирования.

2. Соответствие целям исследования для решения конкретного класса задач, исходя из которых выбираются существенные свойства системы.

Попытки создания универсальной модели, нацеленной на решение большого числа разнообразных задач, приводят к такому усложнению, что она оказывается практически непригодной. Строить модель, приближающуюся по сложности к реальной системе не имеет смысла.

---

3. Абстрагирования от второстепенных деталей - упрощение при сохранении существенных свойств системы. Детализация модели определяется необходимой точностью решения задачи для достижения цели исследования.

Модель должна быть в некоторых отношениях проще прототипа и соответствовать реальной системе по уровню сложности исходя из выбранного множества свойств - игнорируются менее существенные свойства, не оказывающие влияния на решение поставленной задачи, детально рассматриваются основные исследуемые свойства.

4. Блочная структура модели и минимальные связи между блоками с учетом разделения модели по этапам и режимам функционирования системы.

Это дает возможность использования накопленного опыта в процессе отработки модели и многовариантной реализации блоков, отличающихся по точности и сложности, - построения ансамбля моделей.

Подобными явлениями называются такие физические явления, которые одинаковы качественно по форме и по содержанию, т.е. имеют одну физическую природу, развиваются под действием одинаковых сил и описываются одинаковыми по форме дифференциальными уравнениями и краевыми условиями.

Обязательным условием подобия физических явлений должно быть геометрическое подобие систем, где эти явления протекают. Два физических явления будут подобны лишь в том случае, если будут подобны все величины, которые характеризуют их.

Для всех подобных систем существуют безразмерные комплексы величин, которые называются критериями или числами подобия.

Основные положения теории подобия формулируют в виде 3-х теорем подобия.

1 теорема: Подобные явления имеют одинаковые числа подобия.

2 теорема: Любая зависимость между переменными, характеризующая какие-либо явления, может быть представлена, в виде зависимости между числами подобия, составленными из этих переменных. Эта зависимость называется критериальным уравнением.

3 теорема: Подобны те явления, условия однозначности которых подобны, и числа подобия, составленные из условий однозначности, численно равны.

Числа подобия, составленные из величин, входящих в условия однозначности называются определяющими. Числа подобия, в которые входят искомые величины, называются определяемыми.

10. 
    Метод наименьших квадратов. (где используется в мат. моделировании, как с помощью этого метода найти параметры модели, )
    

---

Смотрите также файлы

• Основы информационной безопасности.pdf

• Члены Организации Объединённых Наций, собравшиеся 1 мая 1974 г.docx

• Отчет по преддипломной практике специальности 270802 Строительство и эксплуатация зданий и сооружений.doc

• Международный научный журнал 8 (403) Издается с декабря 2008 г. Выходит еженедельно.pdf

• Лекция 14 учет хозяйственных операций.pdf