Подсистему подготовки сырья вводят в том случае, если сырье по своим характеристикам не соответствует требованиям главной подсистемы. Операторами этой подсистемы являются хранение и транспортировка сырья, нагрев и охлаждение, испарение, плавление, растворение, сушка, измельчение и др.

Подсистема выделения целевого продукта предназначена для разделения реакционной смеси на отдельные компоненты. Операторы подсистемы – ректификация, экстракция, фильтрация и др.

Подсистема обработки технического продукта имеет целью доведение целевого продукта до заданного уровня качества и придания ему товарного вида. В эту подсистему могут быть включены операторы расфасовки, укупорки, маркировки, транспорта, хранения и др.

Энергетическая подсистема включает в себя подсистемы производства энергии, рекуперации энергии и водоподготовки.

Экологическая подсистема предназначена для рекуперации сырья, очистки сточных вод и газовых выбросов.

В состав ХТС кроме элементов включаются еще связи. Связь - это физический канал, по которому происходит обмен веществом, энергией или информацией между элементами (внутренние связи) и между отдельными системами (внешние связи). По физическому смыслу связи бывают материальные, энергетические и информационные.

10. 1   2   3   4

---

Основы математического моделирования элементов ХТС на примере модуля смесителя. (Схема, матер. и тепловой балансы, допущения при моделировании)

В соответствии с исходной задачей, два потока вещества, имеющие расходы G₁ и G₂(моль/сек), температуры T₁ и T₂ (град.К), составы X_1i и X_2i (мольные доли), теплоту Q₁ и Q₂(Вт) подаются в смеситель, откуда выходит один поток с расходом G₃, температурой T₃, составом Х_3i и теплотой Q₃



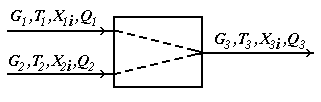
Обычно при составлении упрощенной детерминированной модели принимаются некоторые допущения. Для смесителя, допущения будут следующие:

1. 
   Структура потока в аппарате соответствует режиму идеального смешения; В противном случае, поток на выходе смесителя будет не полностью перемешанный, и, в таком случае необходимо будет либо усложнять модель с учетом коэффициента перемешивания, либо усложнять модель с учетом гидродинамики потоков в аппарате. Это может быть не оправдано по удельным затратам времени на разработку модели, а при неполном учете в модели всех протекающих физико-химических явлений приводить к значительным ошибкам.
   
2. 
   Процесс смешения – адиабатический, не учитывается теплота смешения; В противном случае необходимо учитывать процессы подвода и отвода теплоты, а также теплоту смешения, выделяющуюся при смешении веществ (в особых случаях, в тепловом балансе смесителя требуется учитывать теплоту смешения).
   
3. 
   Все потоки имеют одно фазовое состояние; В противном случае модель нужно будет значительно усложнить, т.к. необходимо использовать смеситель, имеющий 2 или 3 выходных потока (газ, жидкость и твердое), т.к. одним потоком невозможно одновременно выразить различные фазовые состояния, будет необходимо учитывать фазовое равновесие в системе твердое-жидкость-газ, и условия его установления, а также тепловой баланс процессов установления фазового равновесия.
   
4. 
   Давление входных и выходных потоков – одинаковое; При изменении давления могут возникнуть условия, приводящие к изменению фазового состояния
   

---

Общее уравнение материального баланса запишется:



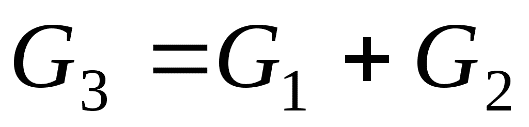
С использованием уравнения материального баланса для вещества можно рассчитать состав выходного потока:



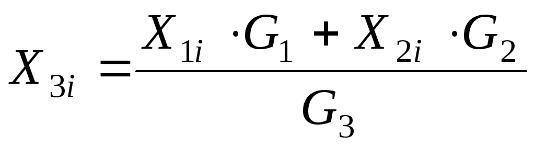
Общее уравнение теплового баланса запишется:



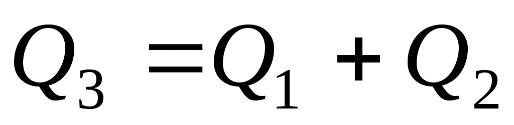
Температура выходного потока рассчитывается методом итераций:

10. 
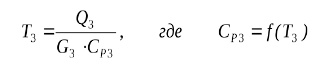
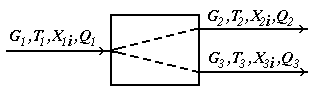
    Основы математического моделирования элементов ХТС на примере модуля делителя. (Схема, матер. и тепловой балансы, допущения при моделировании)
    

Модуль делителя является одним из наиболее простых модулей. В соответствии с исходной задачей, поток вещества, имеющий расход G₁ (моль/сек), температуру T₁ (град.К), составы X_1i (мольные доли) и теплоту Q₁ (Вт) подается в делитель, откуда выходят два потока с расходами G₂ иG₃, температурами T₂ и T₃, составами X_2i и Х_3i и теплотой Q₂ и Q₃



Для делителя, допущения будут следующие:

1. 
   Состав, температура и давление выходных потоков равны составу, температуре и давлению входного потока;
   
2. 
   Все потоки имеют одно фазовое состояние.
   

Известно два способа деления потока. Для ПЕРВОГО способа требуется знать расход первого выходящего потока, а для ВТОРОГО – коэффициент деления потока. В зависимости от типа связанного с делителем оборудования, применяться могут оба способа, однако ПЕРВЫЙ способ имеет ограничения, которые заключаются в том, что используются абсолютные значения, а не относительные. Например, в процессе расчетов, расход входящего потока будет меньше заданного расхода первого выходящего потока, т.е. второй выходящий поток будет иметь отрицательный расход, что невозможно. ВТОРОЙ способ более стабильный в расчетах, т.к. используются относительные значения, однако, в зависимости от типа связанного с делителем оборудования, использование фиксированного коэффициента деления может не соответствовать реальной ХТС.

---

Для реализации ПЕРВОГО способа необходимо знать: расход G₁ (моль/сек), температура T₁ (град.К), состав X_1i (мольные доли) и теплота Q₁ (Вт), также расход первого выходящего потока G₂.

Основное уравнение материального баланса запишется:



Исходя из допущения, состав выходных потоков будет равен составу входного потока:

10. 
    Основы математического моделирования элементов ХТС на примере модуля теплообменника. (Схема, виды теплообменников, матер. и тепловой балансы, основные формулы при расчете параметров теплообменника – алгоритм решения)
    

В отличие от модулей смесителя и делителя, модуль теплообменника не является столь простым, т.к. при изменении температуры потоков возможно изменение их фазового состояния, а, следовательно, при расчете необходимо учитывать такие изменения. В связи с этим, например, только для систем газ-газ, жидкость-жидкость и газ-жидкость различают следующие модели теплообменников:

1. 
   Теплообменник газ-газ или жидкость-жидкость без фазовых переходов (нагреватели и холодильники);
   
2. 
   Теплообменник газ-газ или жидкость-жидкость с фазовым переходом (для системы газ-газ он называется конденсатор, а для системы жидкость-жидкость – испаритель, также существует более сложный вариант, когда тепло от конденсирующегося газа используется для испарения жидкости);
   

Кроме того, так как на процесс расчета теплообменника оказывает влияние его конструкция, то для каждого указанного выше типа теплообменников различают следующие модели:

1. 
   Противоточный ("холодный" и "горячий" агенты идут навстречу друг другу, т.е. противотоком);
   
2. 
   Прямоточный ("холодный" и "горячий" агенты идут параллельно, т.е. прямотоком);
   
3. 
   Перекрестноточный (промежуточный вариант между указанными выше);
   
4. 
   Одноходовой или многоходовой теплообменники (в многоходовых теплообменниках часть труб работает в режиме противотока, а часть – в режиме прямотока, или в многоходовом перекрестноточном теплообменнике жидкость или газ по трубам может двигаться по ходу или против хода потока в межтрубном пространстве);
   
5. 
   Варианты, когда один из агентов (или оба агента) движется за счет естественной конвекции, которые, по интенсивности перемешивания потока за счет естественной конвекции, в свою очередь делятся на горизонтальные и вертикальные;
   
6. 
   Теплообменники смешения ("холодный" и "горячий" агенты непосредственно контактируют друг с другом, например, в аппарате с насадкой).
   

---

И, наконец, теплообменники, различающиеся по режиму работы на:

1. 
   периодические;
   
2. 
   непрерывные.
   

В качестве примера рассмотрим проверочный расчет теплообменника-подогревателя для системы газ-газ, жидкость-жидкость или газ-жидкость с учетом следующих допущений:

• 
  Одноходовой кожухотрубный теплообменник в стационарном режиме;
  
• 
  Теплопередача не сопровождается изменением агрегатного состояния;
  
• 
  Коэффициенты теплоотдачи для "холодного" и "горячего" потоков рассчитывается при начальных температурах теплоносителей;
  
• 
  Схема движения потоков – противоточная;
  
• 
  Потери теплоты отсутствуют.
  

10. 
    Методы поиска оптимума целевой функции. (назвать и рассказать какие основные методы существуют, подробнее остановиться на численных методах: оптимизация перебором, сканирование, метод золотого сечения).
    

Метод множителей Лагранжа  Здесь вместо решения системы конечных уравнений для отыскания оптимума необходимо интегрировать систему диф-ференциальных уравнений. Множители Лагранжа используют так же в качестве вспомога-тельного средства при решении задач с ограничением типа равенств в вариационном исчи-слении и динамическом программировании. Следует особо подчеркнуть, что метод множи-теля Лагранжа позволяют найти лишь необходимые условия существования условного экс-тремума для непрерывных функций, имеющих к тому же непрерывные производные.

Полученные в результате решения значения неизвестных X_i должны быть проверены на экстремум с помощью анализа производных более высокого порядка или другими методами.

Методы вариационного исчисления Оптимальные задачи, когда решение представляется не как совокупность значения конечного числа переменных, а как совокупность функции, вид которых заранее не известен, составляют сущность вариационного исчисления. Вариационное исчисление применяется для оптимизации математически описанных процессов.

---

Смотрите также файлы

• Основы информационной безопасности.pdf

• Члены Организации Объединённых Наций, собравшиеся 1 мая 1974 г.docx

• Отчет по преддипломной практике специальности 270802 Строительство и эксплуатация зданий и сооружений.doc

• Международный научный журнал 8 (403) Издается с декабря 2008 г. Выходит еженедельно.pdf

• Лекция 14 учет хозяйственных операций.pdf