Рис.12

 

На рис.12 показаны в сравнении профили силовой (б) и крепежной (а) резьб. При равной в обоих случаях осевой нагрузке р крепежная резьба имеет большую силу трения в витках. Сила трения в силовой резьбе:

F_б=Pf

Сила трения в крепежной резьбе:

      Fa = Nf =  = Pf¢; f¢ = .

                             f¢ > f;  Fб > Fa.

 

2. По шагу резьбы разделяются на основные и мелкие. Мелкие резьбы для тех же диаметров имеют меньший шаг того же профиля, что и в основной резьбе. Применение мелких резьб меньше ослабляет сечение деталей и благодаря меньшему углу спирали нарезки лучше предохраняет соединение против самоотвинчивания.

Для диаметров свыше 20 мм уже обычно применяются мелкие резьбы.

Пример обозначения резьбы:

М 16 х 2 - основная;    М 16 х 1,5 - мелкая.

Здесь: М - метрическая; 16 - номинальный (наружной) ди аметр резьбы в мм; 2 и 1,5 - шаг резьбы в мм.

 

3. По числу заходов нарезки



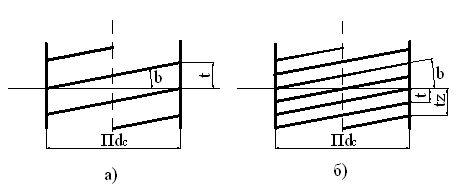
Рис. 13

 

Однозаходные (рис. 13 a) применяются для крепежных деталей.

Многозаходные (рис. 13 б) - обычно для силовых соединений. Угол наклона спирали нарезки b определяется из формул:

для однозаходных резьб -  tgb = ,

для многозаходных резьб - tgb = ,

 где Z - число заходов,  t - шаг, d_c - средний диаметр.

 

4. Цилиндрические и конусные резьбы



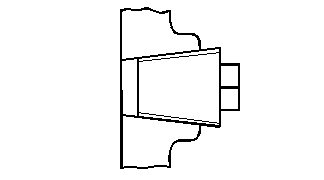
Рис. 14

 

Конусные резьбы (рис.14) применяются там, где необходимо герметически плотное соединение (пробки, трубы, наконечники арматуры). Применяются конусное резьбы как метрической, так и дюймовой системы измерения.

Для возможности свертывания конических резьб с цилиндрическими, биссектриса угла профиля конусной резьбы по ГОСТ перпендикулярна оси.

 

5. Метрические и дюймовые резьбы   

Для нового проектирования резьбы дюймовой системы измерения запрещены; они применяются только для ремонтных целей.

В дюймовых резьбах шаг определяется числом ниток резьбы на дюйм.

 

Элементы крепежных соединений

---

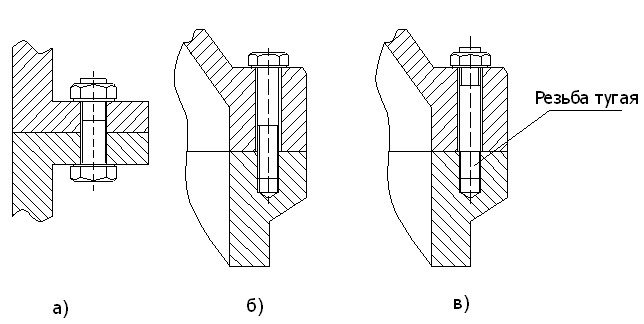
Рис. 15

 

Болт (рис. 15 a) требует для размещения гайки много места что увеличивает габариты и вес конструкции. Зато, при обрыве он легко заменяется.

Винт (рис.15 6) может иметь головку разной формы, в частности и шестигранную. Винт ввертывается в корпус и поэтому требует мало места для размещения,  что сокращает размеры и вес конструкции. Однако, при сборке, резьба в корпусе (в особенности чугунном или алюминиевом) может быть повреждена. При обрыве трудно извлечь оставшуюся в резьбе часть винта.

Шпилька также ввертывается в корпус, для чего имеет с этой стороны тугую нарезку. При разборке свинчивается только гайка и тугая резьба в корпусе не повреждается. Шпильки рекомендуется применять при чугунных или алюминиевых корпусах.

 

Силовые зависимости в резьбовом соединении



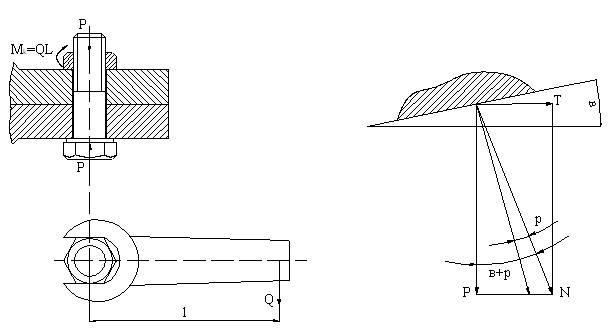
Рис. 16

 

а) зависимость между осевой силой и крутящим моментом на оси винта иди гайки при завинчивании

D_c - средний диаметр трения по торцу головки или гайки;

d_c - средний диаметр резьбы;

M_k - крутящий момент на оси ;

P - осевое усилие;

Т - окружное усилие по среднему диаметру резьбы;

N - нормальное усилие взаимодействия между винтом и гайкой, вектор которого смещен на угол трения r;

f - коэффициент трения в торце;

f₁ - коэффициент трения в резьбе.

tg r = f₁

При завинчивании возникают моменты трения в резьбе и на торце:

M_k = M_рез + M_гор

M_рез = T= Ptg(b+r)

M_гор = Pf

M_k = Ptg(b+r)+ Pf

M_k = P[tg(b+r)+ f]

 

б)   определение КПД резьбы

КПД резьбы определяется отношением идеального момента (без учета сил трения) к реальному моменту (с учетом трения).

КПД - h = 

h = 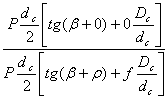 ;                h =  .

 

В частном случае, когда трение в опорах по торцам очень мало (например,  если опорой являются подшипники качения):

h =  .

 

Материал винтовых соединений

Стандартные винты и гайки изготавливаются из Ст.3, иногда Ст.4 и Ст.5, а также сталей: А-12 (автоматная), Ст.20, Ст.35, Ст.45 и других.

---

Для более ответственных напряженных соединений применяются: СТ.40Х, СТ.40ХН и другие. Шайбы пружинные изготавливаются из Ст.65Г с термообработкой, отгибные пластины и проволока для завязывания - из Ст.1.

Распределение нагрузки по виткам резьбы



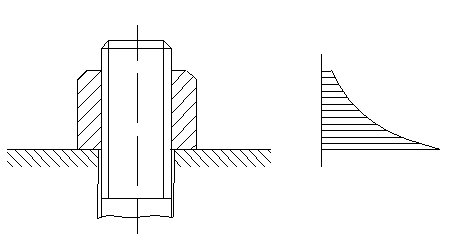
Рис. 17

Распределение нагрузки по виткам резьбы вследствие большой жесткости гайки неравномерно, на рис.17 показана эпюра по Н.Е.Жуковскому. Применив гайку переменной жесткости (показано пунктиром), можно получить более благоприятную эпюру.

 

Расчет винтовых соединений

Опасными напряженными состояниями для болта или винта могут быть следующие:

а) стержень болта - на разрыв по внутреннему сечению резьбы;

б) резьба гайки - на смятие, срез или изгиб;

в) головка болта - на срез.

В стандартных болтах пункты (б) и (в) равнопрочны с пунктом (а), поэтому рассчитывается только стержень на разрыв. Из этих соображений высота головки h=0,7d,    гайки - H=0,8d.

Различают следующие виды резьбовых соединений:

-  ненапряженные, воспринимающие только нагрузку;

- напряженные, которые, кроме действующей нагрузки, воспринимают также усилиe дополнительной затяжки.

 

 

1.       Расчет ненапряженных болтов (винтов)



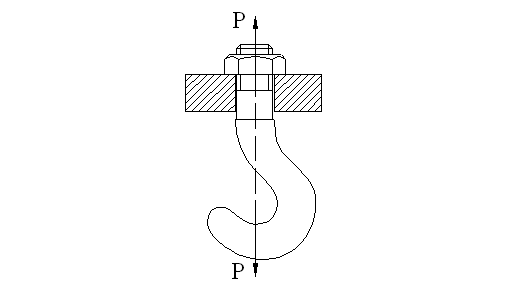
Рис. 18

Напряжение разрыва в стержне болта:

s =   £ [s]

где    P- осевая нагрузка;

Z - число болтов;

d₁ - внутренний диаметр резьбы;

[s] - допускаемое напряжение.

В этой формуле, для упрощения расчетов, приняты некоторые допущения. В действительности явления, происходящие в растянутом стержне болта, более сложны и эпюра распределения напряжений по сечению не вполне равномерна. Эти отклонения учитываются при выборе допускаемых напряжений.

 

2. Расчет напряженных болтов при нагрузке центральной осевой силой

Это соединение осуществляется затяжкой болтов или   гаек при действующей нагрузке. При этом стержень болта дополнительно нагружен касательными напряжениям от крутящего момента, для компенсации действия которых расчетная нагрузка принимается увеличенной на 30%. Усилие затяжки Р_зат = 1,3Р.

s =   £ [s]

 

 

3.Расчет болтов при нагрузке поперечной сдвигающей силой

---

 



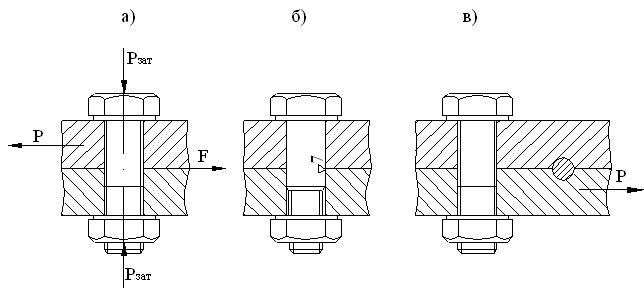
Рис. 19

 

 В этом случае возможны следующие варианты расчета:

 

Вариант А - стандартные болты с зазором (а).

Расчет производится на затяжку соединения осевой силой Р_зат так, чтобы возникающая в стыке сила трения – F противостояла и была равна действию поперечной нагрузки - Р.

F = P = P_зат f

s =   =   £ [s]

    где f - коэффициент трения в стыке; можно принимать f = 0,2;

 Z - число болтов;

1,3 - коэффициент, учитывающий влияние касательных напряжений кручения, возникающих при затяжке в стержне болта.

 

Вариант Б - призонные (плотные) болты или штифты, втулки, шпонки (б), (в)

В этом случае все крепежные отверстия должны быть обработаны (развернуты) в сборе, а болты в отверстиях установлены по плотной посадке. Только при этом обеспечивается восприятие поперечной нагрузки всеми болтами.

Касательное напряжение среза:

t=   £ [t]

Можно принимать [t]  = 0,7[s]

Достоинства варианта А в том, что применяемые при нем болты - стандартные и обеспечивается взаимозаменяемость соединения; недостаток - потребность в большом количестве болтов, которые не всегда можно разместить.

Достоинство варианта Б в малом количестве необходимых для передачи нагрузки болтов; недостаток - потеря взаимозаме няемости при замене одной из соединяемых деталей (например, вследствие износа). Для восстановления соединения необхо димо совместно обработать отверстия на больший размер под болты большего диаметра.



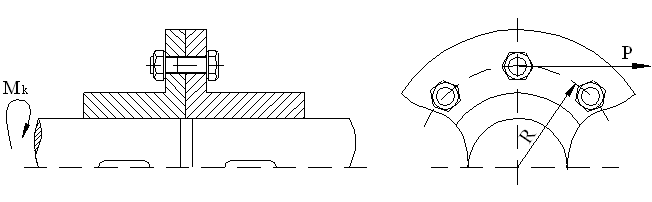
Риc. 20

 

Если соединение нагружено крутящим моментом в плоскости стыка (рис.20), то сначала определяется касательное усилие P =  , которое и является поперечной силой,  а затем поступают так, как указано выше по варианту А или Б.

 

         4. Резьбовые соединения, нагруженные центральной отрывающей силой, когда требуется гарантированная плотность стыка

При действии отрывающей силы Р необходима начальная затяжка, обеспечивающая плотность и жесткость стыка. Часть нагрузки cР дополнительно нагружает винты, остальная часть Р - cР идет на разгрузку стыка. Задача распределения нагрузки между винтом и стыком - статически неопределимая и решается из условий совместной их деформации.

---

Совместная деформация

d = cPl_b = (1-c)Pl_c

l_b и l_c- податливость винта и стыка при действии единичной силы.

Отсюда:

c = 

Податливость винта по закону Гука

l_c = 

 



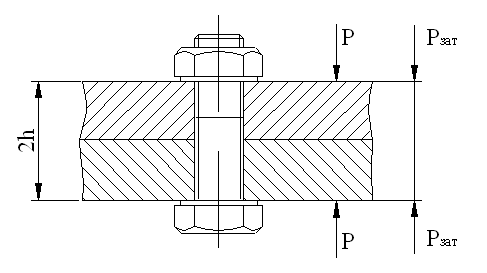
Рис. 21

 

Податливость стыка определяется на основания так называемых конусов давленая (рис.21) опытным путем, например, по опытной формуле:

l_c = 

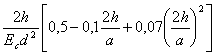
Из условия сохранения плотности (нераскрытия стыка) определяется усилие затяжки:

KP = P_зат + KcP;     P_зат = KP(1 - c).

где К - коэффициент затяжки. Для статической нагрузки К = 1,3+1,5, для динамической -   К= 1,5+l,4.

Расчетная нагрузка:

P_p = 1,3P_зат+cP

 

4а. Расчет болтов крепления крышек резервуаров с внутренним давлением



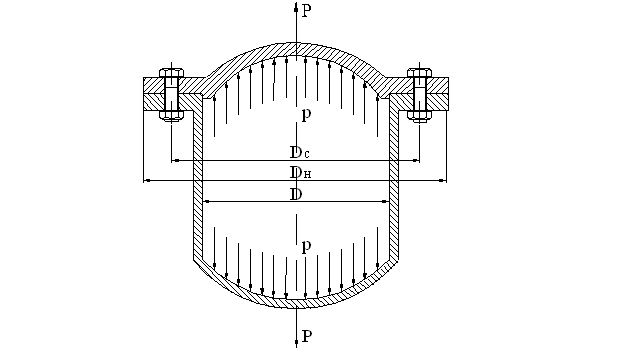
Рис. 22

В этом случае (рис.22) болты должны быть затянуты так, чтобы не только преодолеть нагрузку от сил внутреннего давления, но также дополнительно сжать прокладку для обеспечения герметичности стыка. Усилие затяжки:

P_зат = Р + Р_пр

P_зат =

Здесь: r - внутреннее давление в резервуаре;

К  - коэффициент, учитывающий сжатие прокладки;

К = 2 - 3,5.

Число болтов Z необходимо проверить по условию их размещения на среднем диаметре стыка D_с. Шаг размещения болтов

t = 

должен быть таким, чтобы между болтами оставалось достаточно места для ключа, завертывающего гайку или болт.

 

 

4б. Расчет болтовых соединений при действии отрывающего момента в плоскости перпендикулярной стыку

Нагрузка Р разлагается по осям и дает следующие состав ляющие:

1) нормальная сила

N = Psina

2) касательная сила

Q = Pcos a

3) отрывающий момент

M = Qh = Phcosa

Из условия плотности (нераскрытия) стыка:

s_N =  - нормальные растягиваю щие напряже ния в стыке;

s_U =   - изгибающие напряжения в стыке;

s_зат =  - напряжения затяжки в стыке, которые должны перекрыть действие s

---

Смотрите также файлы

• Геологопоисковые работы на территории Коми асср.pptx

• Геймификация обучения образовательный.pptx

• Конспект для проведения занятия со слушателями Учебного пункта в группе профессиональной подготовки пожарный по дисциплине Экстренная психологическая помощь пострадавшим в чс.doc

• Методические указания к лабораторным работам д ля студентов направления 230700 Прикладная информатика.doc

• Направление подготовки 09. 03.docx