Файл: Учебный курс для студентов очной и заочной форм обучения.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 930
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, в которых выпуклые зубья шестерни зацепляются с вогнутыми зубьями колеса.
К тому же выпуклый и вогнутый профили (обычно круговые) имеют близкие по абсолютной величине радиусы кривизны. За счёт этого получается большая площадка контакта, контактные напряжения уменьшаются и появляется возможность передавать примерно в 1,4 ¸ 1,8 раза большие вращающие моменты.
К сожалению, при этом приходится пожертвовать основным достоинством эвольвентных зацеплений – качением профилей зубьев друг по другу и соответственно получить высокое трение в зубьях. Однако для тихоходных м
ашин это не так важно.
Рабочие боковые поверхности зубьев представляют собой круговинтовые поверхности, поэтому передачи можно называть круговинтовыми. В дальнейшем был разработан вариант передачи с двумя линиями зацепления.
В ней зубья каждого колеса имеют вогнутые ножки и выпуклые головки. Передачи с двумя линиями зацепления обладают большей несущей способностью, менее чувствительны к смещению осей, работают с меньшим шумом и более технологичны. Эти передачи успешно применяются при малых числах зубьев (Z1 < 10) и дают достаточную жёсткость шестерён при их большой относительной ширине.
Зацепления Новикова в редукторах применяют вместо перехода на колёса с твёрдыми поверхностями.
Расчёт передач Новикова на контактную прочность проводят на основе формулы Герца-Беляева, учитывая экспериментально установленный факт, что несущая способность передач при прочих равных условиях обратно пропорциональна синусу угла наклона зубьев. Кроме того, в расчёте немного завышаются допускаемые напряжения.
Передачи бывают однопарные, применяемые в редукторах общего назначения и многопарные, получаемые за счёт увеличения осевого размера и применяемые в прокатных станах, редукторах турбин и т.п.
Конические зубчатые передачи
Передают вращающий момент между валами с пересекающимися осями (чаще всего под углом 900). Их зубья бывают прямыми, косыми, круговыми и обычно имеют эвольвентный профиль.
И
хотя, конические колёса сложнее цилиндрических как по своей геометрии, так и в изготовлении, принципы силового взаимодействия, условия работы, а следовательно, и методика расчёта аналогичны цилиндрическим.
Здесь мы рассмотрим только отличительные особенности расчёта конических колёс.
Сначала конструктор выбирает внешний окружной модуль mte, из которого рассчитывается вся геометрия зацепления, в частности, нормальный модуль в с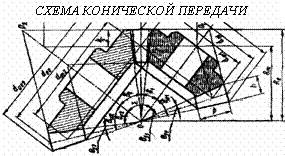
ередине зуба
mnm= mte (1 – 0,5 b/Re),
где Re – внешнее конусное расстояние.
Силы в конической передаче действуют аналогично цилиндрической, однако следует помнить, что из-за перпендикулярности осей радиальная сила на шестерне аналогична осевой силе для колеса и наоборот, а окружная сила при переходе от шестерни к колесу только меняет знак
; .
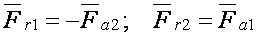Прочностные расчёты конических колёс проводят аналогично цилиндрическим, по той же методике. Из условия контактной выносливости определяют внешний делительный диаметр dwe, из условия прочности на изгиб находят нормальный модуль в середине зуба mnm. При этом в расчёт принимаются воображаемые эквивалентные колёса с числами зубьев Zэ1,2 =Z1,2 / cosd1,2 и диаметрыdэ1,2 = mte Z1,2 / cosd1,2. Здесь Z1, Z2, - фактические числа зубьев конических колёс. При этом числа Zэ1,2могут быть дробными.
В эквивалентных цилиндрических колёсах диаметр начальной окружности и модуль соответствуют среднему сечению конического зуба, вместо межосевого расстояния берётся среднее конусное расстояние, а профили эквивалентных зубьев получают развёрткой дополнительного конуса на плоскость.
Червячные передачи
Относятся в передачам со скрещивающимся осями (рис.3). Она состоит из червяка – винта с трапецеидальной резьбой и зубчатого червячного колеса с зубьями соответствующей специфической формы. Движение в червячной передаче преобразуется по принципу винтовой пары. С положительной стороны червячные передачи характеризуются малыми габаритами, большим передаточный отношением в одной паре и бесшумной работой, однако, вследствие больших потерь мощности на трение в зацеплении, КПД их сравнительно низок и составляет 0,60 + 0,85 (в среднем 0,7 - 0,8). Потери мощности на трение вызывают значительное выделение тепла, которое необходимо отводить от стенок корпуса. Это обстоятельство ограничивает мощность практически применяемых передач пределом 10-20 кВт, зато для малых мощностей эти передачи нашли самое широкое применение.
В отличие от эвольвентных зацеплений, где преобладает контактное качение, виток червяка скользит по зубу колеса. Следовательно, червячные передачи имеют "по определению" один фундаментальный недостаток: высокое трение в зацеплении. Это ведёт к низкому КПД (на 20-30% ниже, чем у зубчатых), износу, нагреву и необходимости применять дорогие антифрикционные материалы.
Кроме того, помимо достоинств и недостатков, червячные передачи имеют важное свойство: движение передаётся только от червяка к колесу, а не наоборот. Никакой вращающий момент, приложенный к колесу, не заставит вращаться червяк. Именно поэтому червячные передачи находят применение в подъёмных механизмах, например в лифтах. Там электродвигатель соединён с червяком, а трос пассажирской кабины намотан на вал червячного колеса во избежание самопроизвольного опускания или падения.
Это свойство не надо путать с реверсивностью механизма. Ведь направление вращения червяка может быть любым, приводя либо к подъёму, либо к спуску той же лифтовой кабины.
Передаточное отношение червячной передачи находят аналогично цилиндрической U = n1 / n2 = Z2 / Z1.
Здесь Z2 – число зубьев колеса, а роль числа зубьев шестерни Z1 выполняет число заходов червяка, которое обычно бывает равно 1, 2, 3 или 4.
Очевидно, что однозаходный червяк даёт наибольшее передаточное отношение, однако наивысший КПД достигается при многозаходных червяках, что связано с уменьшением трения за счёт роста угла трения.
Для увеличения КПД передачи:
1) червяк должен иметь твердую, очень чисто обработанную поверхность зубьев (желательна полировка). Материалом для червяков служат высокоуглеродистые - калимые или мало углеродистые цементированные стали, например, Ст.У-7, У-8, Ст.50 или Ст.20Х, Ст.18ХГТ, Ст.20ХНЗА;
2) венец червячного колеса должен быть изготовлен из антифрикционного материала - бронзы;
3) смазка должна быть обильной в закрытом пыленепроницаемом корпусе.
В СССР стандартизован архимедов червяк (рис.4), который так называется потому, что в торцевом сечении зуб очерчен архимедовой спиралью, а в осевом - прямой, наклонной под углом зацепления a = 20°.
В конволютном червяке режущий инструмент (или наждачный круг) установлен вдоль оси спирали зуба; это удобно при массовом производстве червяков, так как позволяет производить одновременную шлифовку двух сторон профиля зубьев. Эвольвентные червяки применяются сравнительно редко, в них зуб по боковым поверхностям очерчен эвольвентами.
Основные причины выхода из строя червячных передач:
r поверхностное выкрашивание и схватывание;
r излом зуба.
Это напоминает характерные дефекты зубчатых передач, поэтому и расчёты проводятся аналогично.
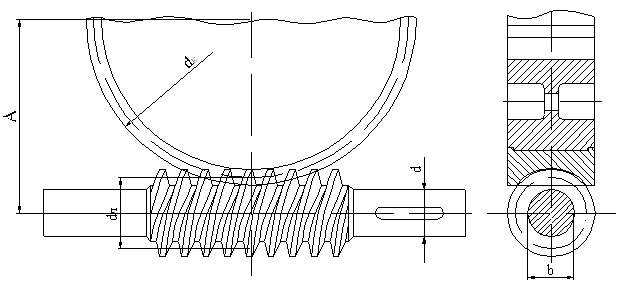
Рис. 3
Геометрическая форма червяков
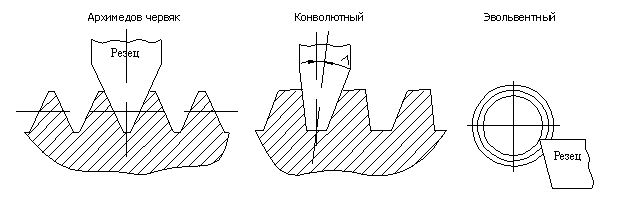
Рис. 4
Расчетные геометрические зависимости
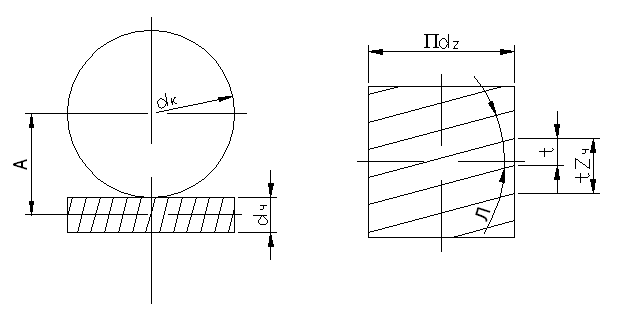
Рис. 5
aк и aч - диаметры делительных окружностей колеса в червяка;
t и m - шаг и модуль (осевой);
Zк Zч - число зубьев колеса и число заходов червяка;
Zч = 1 + 4, обычно Zч = 1 + 2;
l - угол спирала зуба червяка;
qч- относительный диаметр червяка;
qч = 8 –13.
1. Передаточное отношение:
2. Угол наклона спирали нарезки зубьев:
3. Диаметры:
4. Межцентровое расстояние:
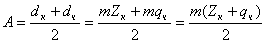
5. Размеры зубьев:
hч = m, hн =1,2m,
КПД червячной передачи
Рассматривая червяк как винт с модульной нарезкой, пренебрегая за малостью потерями в опорах качения, на основании ранее выведенной формулы можно написать:
- угол трения.
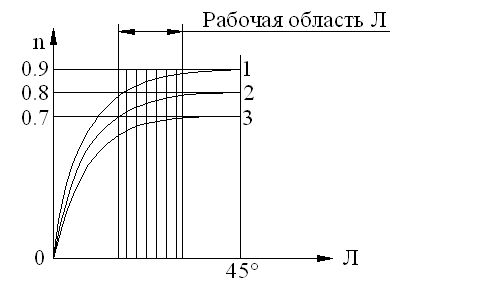
Рис.6
1 - очень хорошие условия - h = 0,8 - 0,85.
2 - средние условия - h = 0,7 - 0,8.
3 - плохие условия (чугунное колесо) - h = 0,6 - 0,7.
Из графика функции (рис.6) видно, что теоретически наивыгоднейшим будет угол l, близкий к 45°, но при таких углах очень велики осевые нагрузки на подшипники колеса, поэтому, учитывая пологость кривых в зоне больших углов, практически принимают рабочую область углов l в пределах, соответствующих Z
ч = 1 + 4.
Силы, действующие в зацеплении червячной передачи
Червячное колесо можно рассматривать как косозубую цилиндрическую шестерню, а схему сил в червячной передаче уподобить схеме сил в косозубых шестернях; отличие заключается лишь в том, что главная нормаль в червячной передаче смещена на угол трения r, который достаточно велик и им пренебрегать нельзя.
1. Окружное усилие для колеса иди осевое - для червяка:
2. Осевое усилие для колеса или окружное - для червяка:
3. Радиальное усилие:
Главная нормаль:
По силам: A, P и R рассчитываются валы и подшипники, сила Рn служит для расчета на прочность зубьев колеса.
Тепловой расчет червячной передачи
Вследствие нагрева, вызванного трением, червячные передачи нуждаются также и в тепловом расчёте. Практика показывает, что механизм опасно нагревать выше 95оС. Допускаемая температура назначается 65 oC.
Уравнение для теплового расчёта составляется из баланса тепловой энергии, а именно: выделяемое червячной парой тепло должно полностью отводиться в окружающую среду
Qвыделяемое = Qотводимое.
Решая это уравнение, находим температуру редуктора, передающего заданную мощность N
t = [860N(1-η)] / [KT S(1-Ψ)] + to.
где KT – коэффициент теплоотдачи, S – поверхность охлаждения (корпус), to – температура окружающей среды, Y – коэффициент теплоотвода в пол.
В случае, когда расчётная температура превышает допускаемую, то следует предусмотреть отвод избыточной теплоты. Это достигается оребрением редуктора, искусственной вентиляцией, змеевиками с охлаждающей жидкостью в масляной ванне и т.д.
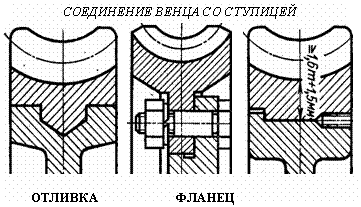Оптимальная пара трения это "сталь по бронзе". Поэтому при стальном червяке червячные колёса должны выполняться из бронзовых сплавов. Однако цветные металлы дороги и поэтому из бронзы выполняется лишь зубчатый венец, который крепится на сравнительно дешёвой стальной ступице. Таким образом, червячное колесо - сборочная единица, где самые популярные способы крепления венца это либо центробежное литьё в кольцевую канавку ступицы; либо крепление венца к ступице болтами за фланец; либо посадка с натягом и стопорение винтами для предотвращения взаимного смещения венца и ступицы.
К тому же выпуклый и вогнутый профили (обычно круговые) имеют близкие по абсолютной величине радиусы кривизны. За счёт этого получается большая площадка контакта, контактные напряжения уменьшаются и появляется возможность передавать примерно в 1,4 ¸ 1,8 раза большие вращающие моменты.
К сожалению, при этом приходится пожертвовать основным достоинством эвольвентных зацеплений – качением профилей зубьев друг по другу и соответственно получить высокое трение в зубьях. Однако для тихоходных м
ашин это не так важно.Рабочие боковые поверхности зубьев представляют собой круговинтовые поверхности, поэтому передачи можно называть круговинтовыми. В дальнейшем был разработан вариант передачи с двумя линиями зацепления.
В ней зубья каждого колеса имеют вогнутые ножки и выпуклые головки. Передачи с двумя линиями зацепления обладают большей несущей способностью, менее чувствительны к смещению осей, работают с меньшим шумом и более технологичны. Эти передачи успешно применяются при малых числах зубьев (Z1 < 10) и дают достаточную жёсткость шестерён при их большой относительной ширине.
Зацепления Новикова в редукторах применяют вместо перехода на колёса с твёрдыми поверхностями.
Расчёт передач Новикова на контактную прочность проводят на основе формулы Герца-Беляева, учитывая экспериментально установленный факт, что несущая способность передач при прочих равных условиях обратно пропорциональна синусу угла наклона зубьев. Кроме того, в расчёте немного завышаются допускаемые напряжения.
Передачи бывают однопарные, применяемые в редукторах общего назначения и многопарные, получаемые за счёт увеличения осевого размера и применяемые в прокатных станах, редукторах турбин и т.п.
Конические зубчатые передачи
Передают вращающий момент между валами с пересекающимися осями (чаще всего под углом 900). Их зубья бывают прямыми, косыми, круговыми и обычно имеют эвольвентный профиль.
И
хотя, конические колёса сложнее цилиндрических как по своей геометрии, так и в изготовлении, принципы силового взаимодействия, условия работы, а следовательно, и методика расчёта аналогичны цилиндрическим.
Здесь мы рассмотрим только отличительные особенности расчёта конических колёс.
Сначала конструктор выбирает внешний окружной модуль mte, из которого рассчитывается вся геометрия зацепления, в частности, нормальный модуль в с
ередине зубаmnm= mte (1 – 0,5 b/Re),
где Re – внешнее конусное расстояние.
Силы в конической передаче действуют аналогично цилиндрической, однако следует помнить, что из-за перпендикулярности осей радиальная сила на шестерне аналогична осевой силе для колеса и наоборот, а окружная сила при переходе от шестерни к колесу только меняет знак
; .Прочностные расчёты конических колёс проводят аналогично цилиндрическим, по той же методике. Из условия контактной выносливости определяют внешний делительный диаметр dwe, из условия прочности на изгиб находят нормальный модуль в середине зуба mnm. При этом в расчёт принимаются воображаемые эквивалентные колёса с числами зубьев Zэ1,2 =Z1,2 / cosd1,2 и диаметрыdэ1,2 = mte Z1,2 / cosd1,2. Здесь Z1, Z2, - фактические числа зубьев конических колёс. При этом числа Zэ1,2могут быть дробными.
В эквивалентных цилиндрических колёсах диаметр начальной окружности и модуль соответствуют среднему сечению конического зуба, вместо межосевого расстояния берётся среднее конусное расстояние, а профили эквивалентных зубьев получают развёрткой дополнительного конуса на плоскость.
Червячные передачи
Относятся в передачам со скрещивающимся осями (рис.3). Она состоит из червяка – винта с трапецеидальной резьбой и зубчатого червячного колеса с зубьями соответствующей специфической формы. Движение в червячной передаче преобразуется по принципу винтовой пары. С положительной стороны червячные передачи характеризуются малыми габаритами, большим передаточный отношением в одной паре и бесшумной работой, однако, вследствие больших потерь мощности на трение в зацеплении, КПД их сравнительно низок и составляет 0,60 + 0,85 (в среднем 0,7 - 0,8). Потери мощности на трение вызывают значительное выделение тепла, которое необходимо отводить от стенок корпуса. Это обстоятельство ограничивает мощность практически применяемых передач пределом 10-20 кВт, зато для малых мощностей эти передачи нашли самое широкое применение.
В отличие от эвольвентных зацеплений, где преобладает контактное качение, виток червяка скользит по зубу колеса. Следовательно, червячные передачи имеют "по определению" один фундаментальный недостаток: высокое трение в зацеплении. Это ведёт к низкому КПД (на 20-30% ниже, чем у зубчатых), износу, нагреву и необходимости применять дорогие антифрикционные материалы.
Кроме того, помимо достоинств и недостатков, червячные передачи имеют важное свойство: движение передаётся только от червяка к колесу, а не наоборот. Никакой вращающий момент, приложенный к колесу, не заставит вращаться червяк. Именно поэтому червячные передачи находят применение в подъёмных механизмах, например в лифтах. Там электродвигатель соединён с червяком, а трос пассажирской кабины намотан на вал червячного колеса во избежание самопроизвольного опускания или падения.
Это свойство не надо путать с реверсивностью механизма. Ведь направление вращения червяка может быть любым, приводя либо к подъёму, либо к спуску той же лифтовой кабины.
Передаточное отношение червячной передачи находят аналогично цилиндрической U = n1 / n2 = Z2 / Z1.
Здесь Z2 – число зубьев колеса, а роль числа зубьев шестерни Z1 выполняет число заходов червяка, которое обычно бывает равно 1, 2, 3 или 4.
Очевидно, что однозаходный червяк даёт наибольшее передаточное отношение, однако наивысший КПД достигается при многозаходных червяках, что связано с уменьшением трения за счёт роста угла трения.
Для увеличения КПД передачи:
1) червяк должен иметь твердую, очень чисто обработанную поверхность зубьев (желательна полировка). Материалом для червяков служат высокоуглеродистые - калимые или мало углеродистые цементированные стали, например, Ст.У-7, У-8, Ст.50 или Ст.20Х, Ст.18ХГТ, Ст.20ХНЗА;
2) венец червячного колеса должен быть изготовлен из антифрикционного материала - бронзы;
3) смазка должна быть обильной в закрытом пыленепроницаемом корпусе.
В СССР стандартизован архимедов червяк (рис.4), который так называется потому, что в торцевом сечении зуб очерчен архимедовой спиралью, а в осевом - прямой, наклонной под углом зацепления a = 20°.
В конволютном червяке режущий инструмент (или наждачный круг) установлен вдоль оси спирали зуба; это удобно при массовом производстве червяков, так как позволяет производить одновременную шлифовку двух сторон профиля зубьев. Эвольвентные червяки применяются сравнительно редко, в них зуб по боковым поверхностям очерчен эвольвентами.
Основные причины выхода из строя червячных передач:
r поверхностное выкрашивание и схватывание;
r излом зуба.
Это напоминает характерные дефекты зубчатых передач, поэтому и расчёты проводятся аналогично.
Рис. 3
Геометрическая форма червяков
Рис. 4
Расчетные геометрические зависимости
Рис. 5
aк и aч - диаметры делительных окружностей колеса в червяка;
t и m - шаг и модуль (осевой);
Zк Zч - число зубьев колеса и число заходов червяка;
Zч = 1 + 4, обычно Zч = 1 + 2;
l - угол спирала зуба червяка;
qч- относительный диаметр червяка;
qч = 8 –13.
1. Передаточное отношение:
2. Угол наклона спирали нарезки зубьев:
3. Диаметры:
4. Межцентровое расстояние:
5. Размеры зубьев:
hч = m, hн =1,2m,
КПД червячной передачи
Рассматривая червяк как винт с модульной нарезкой, пренебрегая за малостью потерями в опорах качения, на основании ранее выведенной формулы можно написать:
- угол трения.
Рис.6
1 - очень хорошие условия - h = 0,8 - 0,85.
2 - средние условия - h = 0,7 - 0,8.
3 - плохие условия (чугунное колесо) - h = 0,6 - 0,7.
Из графика функции (рис.6) видно, что теоретически наивыгоднейшим будет угол l, близкий к 45°, но при таких углах очень велики осевые нагрузки на подшипники колеса, поэтому, учитывая пологость кривых в зоне больших углов, практически принимают рабочую область углов l в пределах, соответствующих Z
ч = 1 + 4.
Силы, действующие в зацеплении червячной передачи
Червячное колесо можно рассматривать как косозубую цилиндрическую шестерню, а схему сил в червячной передаче уподобить схеме сил в косозубых шестернях; отличие заключается лишь в том, что главная нормаль в червячной передаче смещена на угол трения r, который достаточно велик и им пренебрегать нельзя.
1. Окружное усилие для колеса иди осевое - для червяка:
2. Осевое усилие для колеса или окружное - для червяка:
3. Радиальное усилие:
Главная нормаль:
По силам: A, P и R рассчитываются валы и подшипники, сила Рn служит для расчета на прочность зубьев колеса.
Тепловой расчет червячной передачи
Вследствие нагрева, вызванного трением, червячные передачи нуждаются также и в тепловом расчёте. Практика показывает, что механизм опасно нагревать выше 95оС. Допускаемая температура назначается 65 oC.
Уравнение для теплового расчёта составляется из баланса тепловой энергии, а именно: выделяемое червячной парой тепло должно полностью отводиться в окружающую среду
Qвыделяемое = Qотводимое.
Решая это уравнение, находим температуру редуктора, передающего заданную мощность N
t = [860N(1-η)] / [KT S(1-Ψ)] + to.
где KT – коэффициент теплоотдачи, S – поверхность охлаждения (корпус), to – температура окружающей среды, Y – коэффициент теплоотвода в пол.
В случае, когда расчётная температура превышает допускаемую, то следует предусмотреть отвод избыточной теплоты. Это достигается оребрением редуктора, искусственной вентиляцией, змеевиками с охлаждающей жидкостью в масляной ванне и т.д.
Оптимальная пара трения это "сталь по бронзе". Поэтому при стальном червяке червячные колёса должны выполняться из бронзовых сплавов. Однако цветные металлы дороги и поэтому из бронзы выполняется лишь зубчатый венец, который крепится на сравнительно дешёвой стальной ступице. Таким образом, червячное колесо - сборочная единица, где самые популярные способы крепления венца это либо центробежное литьё в кольцевую канавку ступицы; либо крепление венца к ступице болтами за фланец; либо посадка с натягом и стопорение винтами для предотвращения взаимного смещения венца и ступицы.