Файл: Учебный курс для студентов очной и заочной форм обучения.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 897
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Расчет на прочность цилиндрической фрикционной передачи
Проверочный расчет передач с металлическими катками.
Основным критерием работоспособности фрикционных передач с ука занными катками является усталостная прочность. Подставив в формулу (4) формулу Герца (5) для определения наибольших контактных напря жений и выполнив некоторые преобразования, получим формулу прове рочного расчета
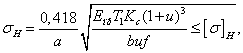 (15)
(15)где а — межосевое расстояние, мм; Епр — приведенный модуль упругости, МПа; f— коэффициент трения (см. табл. 1); Т1 — момент на ведущем валу, Нмм; Кс — коэффициент запаса сцепления; и ≥ 1 — передаточное число; b — рабочая ширина обода катка, мм; — допускаемое контактное напряжение для менее прочного материала, МПа (табл. 2).
Таблица 1. Значения коэффициента трения скольжения для различных материалов
| Материал контактирующей пары | f |
| Сталь по стали или по чугуну (со смазочным материалом) | 0,04-0,05 |
| Чугун (всухую) по: | |
| стали или чугуну | 0,1-0,18 |
| текстолиту | 0,15-0,25 |
| фибре | 0,15-0,30 |
| коже | 0,20-0,50 |
| прессованной бумаге | 0,40-0,50 |
| резине | 0,35-0,70 |
| ферродо | 0,30-0,35 |
Таблица 2. Допускаемые контактные напряжения, модуль упругости для катков из различных материалов
| Материал | | Е |
| МПа | ||
| Закаленная сталь (при хорошем смазывании) | 600-800 | 2,1 · 105 |
| Серый чугун марок от СЧ 10 до СЧЗО | 420—720 | 1,1 · 105 |
| Текстолит | 80-100 | 6 · 103 |
Проектировочный расчет. Подставив выражение (9) в формулу (15) и выполнив некоторые преобразования, получим формулу проекти ровочного расчета для определения межосевого расстояния фрикционной передачи из условия контактной прочности:
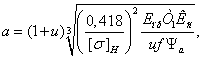 (16)
(16)где — коэффициент ширины обода катка по межосевому расстоянию, .
Проверочный расчет передач с неметаллическими катками (тексто лит, фибра, резина и т. п.). Для этих передач основным критерием рабо тоспособности является износостойкость. Материал не подчиняется зако ну Гука.
Нормальная нагрузка на единицу длины контактных линий
(17)
где T1 — момент на ведущем катке, Нмм; Кс— коэффициент запаса сцеп ления (см. табл.1); u ≥ 1 — передаточное число; b — ширина обода мень шего катка, мм; f — коэффициент трения (см. табл. 1); а - межосевое расстояние, мм; [q] — допускаемая нагрузка на единицу длины контактной линии для менее прочного материала, Н/мм.
Значения [q] для некоторых материалов контактирующих пар (один ма териал сталь или чугун) следующие:
[q], Н/мм
Фибра...........34-39
Резина...........10—30
Кожа.........14,5-24,5
Дерево..........2,4-4,9
Проектировочный расчет.
Подставив в формулу (17) и решив уравнение относительно а, получим формулу проектировочного расчета для определения межосевого расстояния фрикционной передачи из условия износостойкости:
(18)
Последовательность проектировочного расчета.
1. В зависимости от условий работы выбирают материал катков и по табл.2 принимают , Е или для менее прочного материала.
2. По табл.1 задаются коэффициентом трения f, после чего принима ют коэффициент = 0,2 ÷ 0,4; Кс.
3. По формуле (16) или (18) рассчитывают межосевое расстояние.
4. Определяют геометрические размеры катков: D1 — диаметр ведущего катка [формула (7)], D2— ведомого (8); b — ширина обода катков (9).
По формуле (6) уточняют фактическое межосевое расстояние а.
5. По формуле (14) определяют силу нажатия.
6. Передачу проверяют по окружной скорости
v < vmax= (7 ÷ 10) м/с.
7. Проверочный расчет передачи на прочность проводят по формулам: (15) или (17). При этом следует иметь в виду, что допускаемая недогруз ка передачи не более 10 %, перегрузка — не более 5 %.
Коническая фрикционная передача. Устройство и основные геометрические соотношения
Фрикционную передачу с пересекающимися валами и катками, рабо чие поверхности которых конические, называют фрикционной конической пе редачей. На рис. 9 показана фрикционная коническая передача с нерегу лируемым передаточным числом. Ее устройство аналогично цилиндриче ской фрикционной передаче. Прижимной каток конической передачи обычно меньший, так как при этом необходима меньшая сила нажатия. Угол между осями валов (рис. 9) может быть различным. Как правило, межосевой угол передачи
, (19)
где — угол при вершине конуса ведущего катка; — угол при вершине конуса ведомого катка. Для нормальной работы передачи необходимо, что бы общая вершина конусов лежала в точке пересечения геометрических осей валов. Коническая фрикционная передача может быть нереверсивной (чаще) и реверсивной. Ее применяют для передачи небольшой мощности (до 25 кВт).
Геометрические параметры конической фрикционной передачи (см. рис. 9).
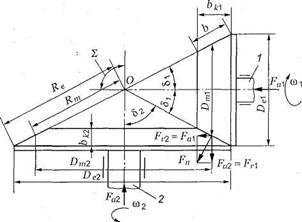
Рис.9. Геометрические параметры конической фрикционной передачи
1. Внешнее конусное расстояние
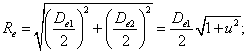 (20)
(20)Среднее конусное расстояние ; т — индекс среднего сечения.
2. Внешний диаметр ведущего катка
3. Диаметр ведомого катка
(22)
2. Длина линии контакта
, (23)
где = 0,25 ÷ 0,3 — коэффициент длины линии контакта.
5. Ширина обода катка
; . (24)
6. Средний диаметр ведущего катка
7. Средний диаметр ведомого катка
отсюда .
Подставив в формулу (20) значение , получим
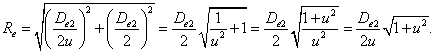
Силы в передаче.
В конической фрикционной передаче действующие силы определяют по размерам средних сечений катков (см. рис.9).
Условие работоспособности для конической фрикционной передачи аналогичное ранее рассмотренному.
Силу нажатия катков определяют по формуле
(27)
где .
Силу Fnможно разложить на осевую Fa2и радиальную Fr2составляю щие (см. рис. 9).
Осевая сила ведущего катка
(28)
ведомого катка
(29)
Радиальные силы катков
; . (30)
Вариаторы
Большинство современных рабочих машин требует регулирования скорости рабочих органов в зависимости от условий осуществления технологического процесса. Для этого машины снабжают ступенчатыми коробками передач с большим числом зубчатых пар, например, в коробке передач автомобилей их 4 - 6 пар, станков 5 - 16 лишь в механизме главного движения. Применение в машинах вариаторов (бесступенчатых передач)значительно упрощает конструкцию, позволяет установить оптимальный скоростной режим и регулировать скорость на ходу. Все это существенно повышает производительность машины, качество продукции и, кроме того, вызывает уменьшение шума и вибрации. Эти достоинства вариаторов обусловили их широкое распространение в различных областях машиностроения (в станках, в машинах пищевой и легкой промышленности, в сельскохозяйственном и дорожном машиностроении и т.д.).
Фрикционный механизм, предназначенный для бесступенчатого регу лирования передаточного числа, называют фрикционным вариатором или про сто вариатором.
Вариаторы можно разделить на следующие группы: клиноременные, цепные и фрикционные.
В данном разделе рассмотрим только фрикционные вариаторы.
Фрикционные вариаторы нашли применение в приводах с малыми габаритами — в станках и транспортных машинах. При рациональном конструировании и тщательном изготовлении они имеют наиболее высокий КПД — до 0,95. Однако надлежащее качество исполнения их возможно только на специализированных заводах.
Вариаторы разделяются на два основных типа:
а) простые, в которых изменяется только один радиус контакта, а другой остается постоянным (лобовой, конусный, дисковый);
б) сложные, в которых изменяются оба радиуса (торовый, шаровой).
Вариаторы выполняют в виде отдельных одноступенчатых механизмов с непосредственным касанием катков без промежуточного диска (см. рис.10) или с промежуточным диском (см. рис.11 и 12).
Предельные передаточные отношения вариатора, будут
и
где D1, d1 и D2, d2 — наибольший и наименьший диаметры ведущего и ведомого колеса; ε — коэффициент скольжения, который зависит от типа и конструкции передачи.
Основной кинематической характеристикой вариатора является диапазон регулирования угло вой скорости (передаточного числа) ведомого вала при постоянной угловой скорости ведущего вала:
Скольжение снижает угловую скорость ведомого вала, но на диапазон регулирования не влияет.
В простых вариаторах передаточное отношение:
В сложных вариаторах передаточное отношение:
Диапазон регулирования:
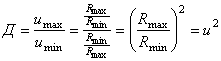 (32)
(32)В сложных вариаторах передаточное отношение может принимать значения, равные:
i > 1; i <1; i = 1.
Диапазон регулирования равен квадрату максимального передаточного отношения. Это значительно расширяет область применения сложных вариаторов.