Файл: Учебнометодический комплекс для проведения практических занятий по дисциплине Управление проектами.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 173
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
, тыс. грн.
Показатель (РР) называет количество базовых периодов, за которые исходные инвестиции будут полностью возвращены за счет генерируемых проектом приливов средств.
Метод расчета коэффициента эффективности инвестиций (ARR)
Метод расчета коэффициента эффективности инвестиций (ARR). Для этого коэффициента характерны следующие признаки:
Алгоритм расчета очень простой, что и определяет распространенное использование этого показателя на практике:
PN
ARR= (2.7)
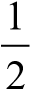 (Inv−RY)
(Inv−RY)
где РN - среднегодовой доход (прибыль с учетом отчислений в
бюджет);
RY - остаточная или ликвидационная стоимость.
Средний размер капиталовложений находится делением исходной суммы капитальных вложений на два, если предполагается, что по истечении срока реализации анализируемого проекта все капитальные затраты будут списаны; если предполагается наличие остаточной или ликвидационной стоимости (RY), то ее оценка должна быть исключена.
Этот показатель, как правило, сравнивают со средним уровнем рентабельности, которую устанавливает предприятие, например, рентабельностью авансированного капитала.
Коэффициент рентабельности авансированного капитала (Ра) рассчитывается по формуле:
Pa =∑ЧП (2.8)
∑АС
где ΣЧП - общая чистая прибыль предприятия;
ΣАС - общая сумма средств, авансированная в деятельность предприятия.
Если ARR> Ра, то проект целесообразен.
Этот метод расчета коэффициента эффективности инвестиций имеет следующие недостатки:
2.2.2 Сравнительный анализ проектов различной продолжительности
В реальной жизни вполне вероятна ситуация
, когда необходимо сравнить проекты различной продолжительности. Например, проекты А и Б расчитаны соответственно на i и j лет. В данном случне рекомендуется:
= НЗК (i, j) ;
Суммарный чистый дисконтированный доход (NPV) повторяющегося проекта рассчитывается по формуле:
I способ:
где NPVi - чистый дисконтированный доход выходного проекта;
i - длительность выходного проекта;
где r - значение коэффициента дисконтирования в долях единицы; n - количество повторений исходного проекта (оно характеризует количество слагаемых в скобках).
rР i rН = (1+ )×(1+ )−1 (2.11)
100 100
где rн - номинальная норма прибыли,%; rр - реальная норма прибыли,%; i - ставка инфляции,%
Существует два способа оценки NPV - по номинальной или реальной ставками. Самое главное, чтобы ставки дисконтирования и денежные потоки от капитальных вложений, используемые при расчете, соответствовали друг другу. То есть, если берутся за основу номинальные денежные потоки, то дисконтировать их нужно по номинальной дисконтной ставке и аналогично для реальных денежных потоков.
0>1>
Задача 1
Определьть целесообразность инвестирования на приобретениепредприятия и налаживания производства металлопродукции по исходным данным, приведенным в таблице 2.1.
Таблица 2.1 – Исходные данные по вариантам к задаче 1
Продолжение таблицы 2.1
Продолжение таблицы 2.1
Продолжение таблицы 2.1
Показатель (РР) называет количество базовых периодов, за которые исходные инвестиции будут полностью возвращены за счет генерируемых проектом приливов средств.
Метод расчета коэффициента эффективности инвестиций (ARR)
Метод расчета коэффициента эффективности инвестиций (ARR). Для этого коэффициента характерны следующие признаки:
-
во - первых, доход характеризуется показателем чистой прибыли; -
во - вторых, не подразумевает дисконтирования дохода.
Алгоритм расчета очень простой, что и определяет распространенное использование этого показателя на практике:
PN
ARR= (2.7)
где РN - среднегодовой доход (прибыль с учетом отчислений в
бюджет);
RY - остаточная или ликвидационная стоимость.
Средний размер капиталовложений находится делением исходной суммы капитальных вложений на два, если предполагается, что по истечении срока реализации анализируемого проекта все капитальные затраты будут списаны; если предполагается наличие остаточной или ликвидационной стоимости (RY), то ее оценка должна быть исключена.
Этот показатель, как правило, сравнивают со средним уровнем рентабельности, которую устанавливает предприятие, например, рентабельностью авансированного капитала.
Коэффициент рентабельности авансированного капитала (Ра) рассчитывается по формуле:
Pa =∑ЧП (2.8)
∑АС
где ΣЧП - общая чистая прибыль предприятия;
ΣАС - общая сумма средств, авансированная в деятельность предприятия.
Если ARR> Ра, то проект целесообразен.
Этот метод расчета коэффициента эффективности инвестиций имеет следующие недостатки:
-
не учитывает временной составляющей денежных потоков; -
не оказывает разграничения между проектами с одинаковой суммой среднегодовой прибыли, хотя сумма прибыли по годам может очень различаться; -
не различает проекты, которые имеют одинаковый среднего-довой доход, и эта сумма может генерировать в течение различного количества лет и др.
2.2.2 Сравнительный анализ проектов различной продолжительности
В реальной жизни вполне вероятна ситуация
, когда необходимо сравнить проекты различной продолжительности. Например, проекты А и Б расчитаны соответственно на i и j лет. В данном случне рекомендуется:
-
найти наименьшее общее кратное сроков действия проектов z
= НЗК (i, j) ;
-
рассмотреть каждый из проектов как повторяющийся, проана-лизувать NPV проектов А и Б, реализованных необходимое количество раз в течение периода z; -
выбрать тот проект из исходных, для которого суммарное NPV повторяющегося потока имеет наибольшее значение.
Суммарный чистый дисконтированный доход (NPV) повторяющегося проекта рассчитывается по формуле:
| 1 1 1 NPV(i,n) = NPVi ⋅(1+ i + 2i + 3i + (1+ r) (1+ r) (1+ r) | 1 + ) ni (1+ r) |
| II способ: | (.9) |
| (1+ r)i NPV(i,n) = NPVi ⋅ i (1+ r) −1 | (2.10) |
I способ:
где NPVi - чистый дисконтированный доход выходного проекта;
i - длительность выходного проекта;
где r - значение коэффициента дисконтирования в долях единицы; n - количество повторений исходного проекта (оно характеризует количество слагаемых в скобках).
rР i rН = (1+ )×(1+ )−1 (2.11)
100 100
где rн - номинальная норма прибыли,%; rр - реальная норма прибыли,%; i - ставка инфляции,%
Существует два способа оценки NPV - по номинальной или реальной ставками. Самое главное, чтобы ставки дисконтирования и денежные потоки от капитальных вложений, используемые при расчете, соответствовали друг другу. То есть, если берутся за основу номинальные денежные потоки, то дисконтировать их нужно по номинальной дисконтной ставке и аналогично для реальных денежных потоков.
0>1>
Учебные задания
Задача 1
Определьть целесообразность инвестирования на приобретениепредприятия и налаживания производства металлопродукции по исходным данным, приведенным в таблице 2.1.
Таблица 2.1 – Исходные данные по вариантам к задаче 1
| Показатели | Исходные данные по вариантам | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1. Сумма инвестиций на приобретение предприятия и налаживания производства металлопродукции, млн. грн. | 2,5 | 8,6 | 8,7 | 9,2 | 8,0 | 9,8 | 9,4 | 8,9 | 9,9 | 8,7 |
| 2. Стоимость реконструкции предприятия перед началом производства, тыс. грн. | 300 | 338 | 475 | 390 | 326 | 445 | 478 | 412 | 480 | 433 |
| 3 Предполагается сохранить | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| профиль деятельности предприятия в течение срока (период реализации инвестиционного проекта), лет | | | | | | | | | | |
| 4. Средняя себестоимость изделия, грн. | 24 | 34 | 39 | 30 | 38 | 34 | 39 | 33 | 30 | 37 |
| 5. Отпускная цена изделия, грн. | 30 | 47 | 45 | 45 | 41 | 44 | 46 | 40 | 47 | 41 |
| 6. Ежегодные объемы выпуска, тис. шт. | 800 | 618 | 721 | 727 | 638 | 745 | 616 | 670 | 751 | 758 |
| 7. Амортизационные отчисления по всем группам основных фондов составят в год, тыс. грн. | 200 | 297 | 272 | 203 | 255 | 200 | 297 | 212 | 203 | 266 |
| 8. Дисконтная ставка, % | 8 | 11 | 12 | 11 | 13 | 15 | 15 | 13 | 15 | 10 |
Продолжение таблицы 2.1
| Показатели | Исходные данные по вариантам | |||||||||
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 1. Сумма инвестиций на приобретение предприятия и налаживания производства металлопродукции, млн. грн. | 8,1 | 8,9 | 8,9 | 8,9 | 9,4 | 9,7 | 8,5 | 8,8 | 9,2 | 8,3 |
| 2. Стоимость реконструкции предприятия перед началом производства, тыс. грн. | 340 | 443 | 421 | 480 | 449 | 397 | 461 | 495 | 313 | 425 |
| 3 Предполагается сохранить профиль деятельности предприятия в течение срока (период реализации инвестиционного проекта), лет | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 4. Средняя себестоимость изделия, грн. | 37 | 33 | 36 | 35 | 37 | 36 | 38 | 32 | 32 | 40 |
| 5. Отпускная цена изделия, грн. | 46 | 42 | 42 | 41 | 42 | 41 | 44 | 45 | 46 | 44 |
| 6. Ежегодные объемы выпуска, тис. шт. | 612 | 793 | 783 | 670 | 793 | 729 | 706 | 682 | 737 | 700 |
| 7. Амортизационные отчисления по всем группам основных фондов составят в | 219 | 231 | 206 | 226 | 271 | 247 | 244 | 294 | 241 | 247 |
| год, тыс. грн. | | | | | | | | | | |
| 8. Дисконтная ставка, % | 12 | 14 | 12 | 13 | 12 | 11 | 13 | 13 | 13 | 15 |
Продолжение таблицы 2.1
| Показатели | Исходные данные по вариантам | |||||||||
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| 1. Сумма инвестиций на приобретение предприятия и налаживания производства металлопродукции, млн. грн. | 2,5 | 9,4 | 8,4 | 8,9 | 9,5 | 8,3 | 9,4 | 10,0 | 9,2 | 8,7 |
| 2. Стоимость реконструкции предприятия перед началом производства, тыс. грн. | 300 | 467 | 428 | 355 | 433 | 321 | 428 | 421 | 407 | 449 |
| 3 Предполагается сохранить профиль деятельности предприятия в течение срока (период реализации инвестиционного проекта), лет | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 4. Средняя себестоимость изделия, грн. | 24 | 37 | 30 | 35 | 37 | 31 | 31 | 37 | 33 | 39 |
| 5. Отпускная цена изделия, грн. | 30 | 42 | 45 | 40 | 43 | 42 | 43 | 45 | 41 | 43 |
Продолжение таблицы 2.1
| Показатели | Исходные данные по вариантам | |||||||||
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| 6. Ежегодные объемы выпуска, тис. шт. | 800 | 699 | 634 | 723 | 670 | 624 | 609 | 625 | 633 | 730 |
| 7. Амортизационные отчисления по всем группам основных фондов составят в год, тыс. грн. | 200 | 243 | 256 | 299 | 226 | 280 | 222 | 212 | 270 | 217 |
| 8. Дисконтная ставка, % | 8 | 10 | 14 | 11 | 13 | 12 | 10 | 11 | 11 | 11 |