Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

Моделирование экономических процессов


Группа Сд18М161

Студент
А.Ю. Малыгин

МОСКВА 2022

Практические занятия

Задание 1
Составить план производства продукции, обеспечив максимум прибыли, учитывая ограничения, заданные в таблице 1.

Таблица 1. Линейная оптимизация

	Расход сырья (доли)					Прибыль от реализации единицы продукции, руб.
	Сырье 1	Сырье 2	Сырье 3	Сырье 4
Продукт 1	0,2	0,3	0,1	0,4	120
Продукт 2	0,4	0,1	0,3	0,2	150
Продукт 3	0,6	0,1	0,1	0,2	110
Наличие сырья на складе, кг	850	640	730	1000

Решение
1) Составим экономико-математическую модель задачи.

Объектом моделирования является процесс получения максимальной прибыли, а целью – оптимизация структуры и объема производства продукции.

Задача относится к классу оптимизационных задач. Математическая модель для задач такого класса состоит в построении целевой функции, для которой надо найти экстремум, при ограничениях.

---

Для решения поставленной задачи введем обозначения:

х₁ – объем производства продукта 1-го вида;

х₂ – объем производства продукта 2-го вида;

х₃ – объем производства продукта 3-го вида.

Общую прибыль от реализации продукции можно определить по формуле:

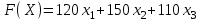(руб.)

Функция F называется целевой, ее следует максимизировать. Поэтому получаем:



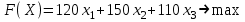
На целевую функцию накладываются следующие ограничения:

а) ограничение по запасу сырья 1:

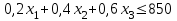(кг);

б) ограничение по запасу сырья 2:

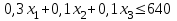(кг);

в) ограничение по запасу сырья 3:

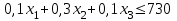(кг);

г) ограничение по запасу сырья 4:

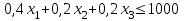(кг);

д) условия неотрицательности объемов производства каждого вида продукции:

.

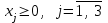Математическая модель задачи: составить оптимальную производственную программу (х₁, х₂, х₃), обеспечивающую максимальную прибыль от реализации продукции:



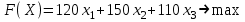
при ограничениях:



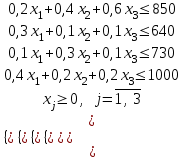
Математическая модель задачи линейного программирования составлена.
2) Определим оптимальный план производства продукции с помощью симплекс-метода.

Сначала приведем задачу к канонической форме.

Чтобы перейти от общей формы записи задачи линейного программирования к канонической, нужно ограничения-неравенства исходной задачи линейного программирования преобразовать в ограничения-равенства добавлением к их левой части дополнительной неотрицательной переменной со знаком «+» в случае неравенства вида «» и со знаком «-» - в случае неравенства вида «».

В первое ограничение системы добавим переменную 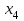со знаком «+», во второе ограничение системы добавим переменную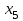

---

со знаком «+», в третье ограничение системы добавим переменную 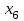со знаком «+» и в четвертое ограничение системы добавим переменную 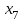со знаком «+». В результате получаем следующую систему ограничений: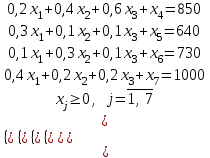



Следовательно, исходная задача может быть записана в канонической форме так: найти максимум функции



при ограничениях:



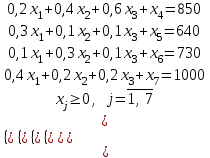
В полученной системе уравнений системы ограничений имеются четыре базисные переменные. Решим систему уравнений относительно базисных переменных x₄, x₅, x₆ и x₇. Предположим, что свободные переменные равны 0 и получим первый опорный план:

.

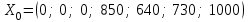Ему соответствует значение целевой функции, равное:

.

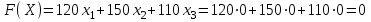Составим исходную симплекс-таблицу:

Базис	Свободный член	x1	x2	x3	x4	x5	x6	x7	Симплекс-отношение
x4	850	0,2	0,4	0,6	1	0	0	0	850/0,4=2125
x5	640	0,3	0,1	0,1	0	1	0	0	640/0,1=6400
x6	730	0,1	0,3	0,1	0	0	1	0	730/0,3=2433,333
x7	1000	0,4	0,2	0,2	0	0	0	1	1000/0,2=5000
F(X0)	0	-120	-150	-110	0	0	0	0

---

Переходим к основному алгоритму симплекс-метода.

Итерация 1. Текущий опорный план не является оптимальным, так как в индексной строке находятся отрицательные коэффициенты.

В индексной строке F(Х) выбираем максимальный по модулю отрицательный элемент. В качестве генерального столбца будет выступать x₂. Вычислим значения D_i по строкам как частное от деления: b_i / a_i2 и из них выберем наименьшее:

.

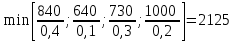Таким образом, строка х₄ является генеральной. Разрешающий элемент равен РЭ = 0,4 и находится на пересечении генерального столбца и генеральной строки.

Формируем следующую часть симплексной таблицы. Вместо переменной x₄ в план 1 войдет переменная x₂.

Строка, которая соответствует переменной x₂ в плане 1, получена в результате деления всех элементов строки x₄ плана 0 на разрешающий элемент РЭ=0,4. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₂ записываем нули.

Все остальные элементы нового плана, включая элементы индексной строки, определяем по правилу прямоугольника.

Элементы разрешающей строки делим на разрешающий элемент и записываем в соответствующей по номеру строке новой таблицы:

, при i = r.

Все остальные элементы новой таблицы рассчитываем по формулам:

, при i ≠ r

где - элемент новой симплекс-таблицы, a_ij, - элемент предыдущей симплекс-таблицы, a_rk - разрешающий элемент, a_ik - элемент разрешающего столбца, a_rj - элемент разрешающей строки.

Представим расчет каждого элемента в виде таблицы:

Базис	Свободный член	x1	x2	x3
x2	850 / 0,4	0,2 / 0,4	0,4 / 0,4	0,6 / 0,4
x5	640-(850*0,1)/0,4	0,3-(0,2*0,1)/0,4	0,1-(0,4*0,1)/0,4	0,1-(0,6*0,1)/0,4
x6	730-(850*0,3)/0,4	0,1-(0,2*0,3)/0,4	0,3-(0,4*0,3)/0,4	0,1-(0,6*0,3)/0,4
x7	1000-(850*0,2)/0,4	0,4-(0,2*0,2)/0,4	0,2-(0,4*0,2)/0,4	0,2-(0,6*0,2)/0,4
F(X1)	0-(850*(-150))/0,4	-120-(0,2*(-150))/0,4	-150-(0,4*(-150))/0,4	-110-(0,6*(-150))/0,4

---

Базис	x4	x5	x6	x7
x2	1 / 0,4	0 / 0,4	0 / 0,4	0 / 0,4
x5	0-(1*0,1)/0,4	1-(0*0,1)/0,4	0-(0*0,1)/0,4	0-(0*0,1)/0,4
x6	0-(1*0,3)/0,4	0-(0*0,3)/0,4	1-(0*0,3)/0,4	0-(0*0,3)/0,4
x7	0-(1*0,2)/0,4	0-(0*0,2)/0,4	0-(0*0,2)/0,4	1-(0*0,2)/0,4
F(X1)	0-(1*(-150))/0,4	0-(0*(-150))/0,4	0-(0*(-150))/0,4	0-(0*(-150))/0,4

После перерасчета получаем новую таблицу:

Базис	Свободный член	x1	x2	x3	x4	x5	x6	x7	Симплекс-отношение
x2	2125	0,5	1	1,5	2,5	0	0	0	2125/0,5=4250
x5	427,5	0,25	0	-0,05	-0,25	1	0	0	427,5/0,25=1710
x6	92,5	-0,05	0	-0,35	-0,75	0	1	0	-
x7	575	0,3	0	-0,1	-0,5	0	0	1	575/0,3=1916,667
F(X1)	318750	-45	0	115	375	0	0	0

---

Смотрите также файлы

• Систематизация средневековой философской мысли в трудах Формы Аквинского.docx

• Химическое название.pdf

• Деятельность фирмы в условиях совершенной конкуренции.docx

• Решение задач в два действия.docx

• Наш знаменитый земляк.docx