Этап 2. Выполним переход к новому допустимому решению.

1) Выбираем клетку (3;1).

2) Для клетки (3;1) «организуем цикл»: соединим ее с помощью многоугольника с занятыми клетками: (3;2), (1;2), (1;4), (2;4), (2;1).

3) Расставляем в выделенных клетках «+» и «-»: в свободной клетке (3;1) «+», а в остальных по порядку «-», «+»:

	Тарифы по перемещению единицы груза, тыс.руб.
	Потребитель1	Потребитель2	Потребитель3	Потребитель4	Возможности поставщика
Поставщик1	7	4[150][+]	9	3[250][-]	400
Поставщик2	2[450][-]	11	8	4[100][+]	550
Поставщик 3	3[+]	8[100][-]	6[200]	5	300
Потребности потребителя	450	250	200	350

4) В клетках со знаком «-» выбираем наименьшее значение:

min (250; 450; 100) = 100.

5) Данное наименьшее значение прибавляем в клетки со знаком «+» к объемам перевозок и вычитаем в клетках со знаком «-». Свободная клетка становится занятой, а клетка с объемом перевозок 0 – свободной.

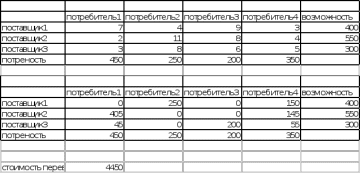
В результате получаем новый план перевозок:

	Тарифы по перемещению единицы груза, тыс.руб.
	Потребитель1	Потребитель2	Потребитель3	Потребитель4	Возможности поставщика
Поставщик1	7	4[250]	9	3[150]	400
Поставщик2	2[350]	11	8	4[200]	550
Поставщик 3	3[100]	8	6[200]	5	300
Потребности потребителя	450	250	200	350

---

Матрица перевозок груза имеет вид:



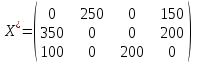
Вычислим значение целевой функции для построенного плана:

.

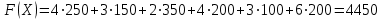Возвращаемся к этапу 1.

Итерация 3.

Этап 1. Проверим оптимальность опорного плана.

Для занятых клеток составим систему уравнений потенциалов:

u₁ + v₂ = 4; u₁ = 0; v₂ = 4;

u₁ + v₄ = 3; 0 + v₄ = 3; v₄ = 3;

u₂ + v₄ = 4; 3 + u₂ = 4; u₂ = 1;

u₂ + v₁ = 2; 1 + v₁ = 2; v₁ = 1;

u₃ + v₁ = 3; 1 + u₃ = 3; u₃ = 2;

u₃ + v₃ = 6; 2 + v₃ = 6; v₃ = 4.

Для каждой свободной клетки найдем оценку:

∆₁₁ = u₁ + v₁ - с₁₁ = 0 + 1 - 7 = -6 < 0;

∆₁₃ = u₁ + v₃ - с₁₃ = 0 + 4 - 9 = -5 < 0;

∆₂₂ = u₂ + v₂ - с₂₂ = 1 + 4 - 11 = -6 < 0;

∆₂₃ = u₂ + v₃ - с₂₃ = 1 + 4 - 8 = -3 < 0;

∆₃₂ = u₃ + v₂ - с₃₂ = 2 + 4 - 8 = -2 < 0;

∆₃₄ = u₃ + v₄ - с₃₄ = 2 + 3 - 5 = 0.

Среди оценок есть нет положительных, поэтому решение оптимально.

Таким образом, оптимальный план перевозок груза:



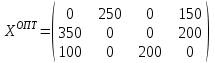
Минимальные затраты на перевозку груза составят:

.

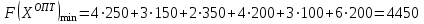Ответ. Груз, находящийся у 1-го поставщика, требуется доставить 2-му потребителю в количестве 250 единиц и 4-му потребителю в количестве 150 единиц.

Груз, находящийся у 2-го поставщика, требуется доставить 1-му потребителю в количестве 350 единиц и 4-му потребителю в количестве 200 единиц.

Груз, находящийся у 3-го поставщика, требуется доставить 1-му потребителю в количестве 100 единиц и 3-му потребителю в количестве 200 единиц.

При использовании данного плана перевозок груза суммарные затраты на перевозку груза будут минимальными и составят 4450 тыс.руб.

---

Смотрите также файлы

• Систематизация средневековой философской мысли в трудах Формы Аквинского.docx

• Химическое название.pdf

• Деятельность фирмы в условиях совершенной конкуренции.docx

• Решение задач в два действия.docx

• Наш знаменитый земляк.docx