Итерация 2. Текущий опорный план не является оптимальным, так как в индексной строке находится отрицательный коэффициент.

В качестве генерального столбца будет выступать x₁. Вычислим значения D_i по строкам как частное от деления: b_i / a_i1 и из них выберем наименьшее:

.

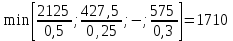Таким образом, строка х₅ является генеральной. Разрешающий элемент равен РЭ = 0,25. Формируем следующую часть симплексной таблицы. Вместо переменной x₅ в план 2 войдет переменная x₁.

Строка, соответствующая переменной x₁ в плане 2, получена в результате деления всех элементов строки x₅ плана 1 на разрешающий элемент РЭ=0,25. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₁ записываем нули.

После перерасчета получаем новую таблицу:

Базис	Свободный член	x1	x2	x3	x4	x5	x6	x7
x2	1270	0	1	1,6	3	-2	0	0
x1	1710	1	0	-0,2	-1	4	0	0
x6	178	0	0	-0,36	-0,8	0,2	1	0
x7	62	0	0	-0,04	-0,2	-1,2	0	1
F(X2)	395700	0	0	106	330	180	0	0

---

Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальное решение задачи.

Таким образом, получаем:

x₁ = 1710; x₂ = 1270; x₃ = 0.

Найдем максимальное значение целевой функции:

.

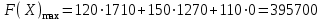Ответ. 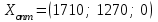; 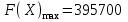. Для получения максимальной прибыли необходимо производить 1710 кг продукта 1-го вида и 1270 кг продукта 2-го вида, а продукт 3-го вида производить не требуется. При использовании данного плана производства прибыль от реализации продукции будет максимальной и составит 395700 руб.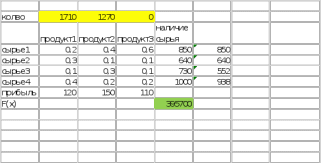


Задание 2
Распределить план перевозок однотипного груза от трёх поставщиков к четырём потребителям, обеспечив минимальные затраты на перевозку.

Исходные данные представлены в таблице 2.

Таблица 2. Транспортная задача.

	Тарифы по перемещению единицы груза, тыс.руб.
	Потребитель1	Потребитель2	Потребитель3	Потребитель4	Возможности поставщика
Поставщик1	7	4	9	3	400
Поставщик2	2	11	8	4	550
Поставщик 3	3	8	6	5	300
Потребности потребителя	450	250	200	350

Решение
1) Построим математическую модель представленной транспортной задачи.

Обозначим через х_ij – объем перевозки груза от i-го поставщика к j-му потребителю. Тогда суммарные затраты на перевозку груза F(Х) составит:

---

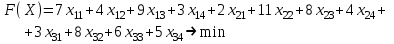
Проверим тип представленной транспортной задачи:

;

.

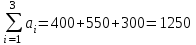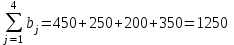Так как 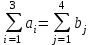, то данная задача является закрытой.

Заданные возможности поставщиков и потребности потребителей накладывают ограничения на значения объемов перевозок груза x_ij.

Ограничения по возможностям поставщиков:



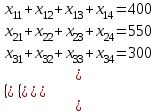
Ограничения по объемам потребностей потребителей:



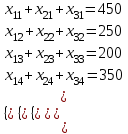
Объемы перевозимого груза не могут быть отрицательными:

.

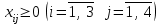Математическая модель представленной транспортной задачи составлена.
2) Построим опорный (базисный) план перевозок методом «минимальной стоимости» («минимального тарифа»).

Выбираем клетку с минимальным тарифом. Искомый элемент равен c₂₁=2. Для этого элемента возможность поставщика равна 550, а потребность потребителя составляет 450. Поскольку минимальным значением является 450, то вычитаем данное значение:

x₂₁ = min(550, 450) = 450.

Далее искомый элемент равен c₁₄=3. Для этого элемента возможность поставщика равна 400, а потребность потребителя составляет 350. Поскольку минимальным значением является 350, то вычитаем данное значение:

x₁₄ = min(400, 350) = 350.

Аналогично определяем остальные элементы:

x₁₂ = min(50, 250) = 50; x₃₃ = min(300, 200) = 200;

x₃₂ = min(100, 200) = 100; x₂₂ = 100.

В результате получен опорный план, который является допустимым, так как соответствует системе ограничений транспортной задачи:

	Тарифы по перемещению единицы груза, тыс.руб.
	Потребитель1	Потребитель2	Потребитель3	Потребитель4	Возможности поставщика
Поставщик1	7	4[50]	9	3[350]	400
Поставщик2	2[450]	11[100]	8	4	550
Поставщик 3	3	8[100]	6[200]	5	300
Потребности потребителя	450	250	200	350

---

Таким образом, опорный план перевозок груза имеет вид:



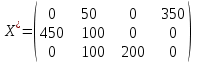
Вычислим значение целевой функции (общие затраты на перевозку груза) для построенного плана:

.

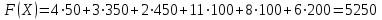Число занятых клеток таблицы равно 8. Их должно быть m + n - 1 = 3 + 4 - 1 = 6, поэтому опорный план является невырожденным.
3) Найдем оптимальный план перевозок методом потенциалов и соответствующие ему минимальные транспортные затраты.

Итерация 1.

Этап 1. Проверим оптимальность опорного плана.

Для занятых клеток составим систему уравнений потенциалов:

u₁ + v₂ = 4; u₁ = 0; v₂ = 4;

u₂ + v₂ = 11; 4 + u₂ = 11; u₂ = 7;

u₂ + v₁ = 2; 7 + v₁ = 2; v₁ = -5;

u₃ + v₂ = 8; 4 + u₃ = 8; u₃ = 4;

u₃ + v₃ = 6; 4 + v₃ = 6; v₃ = 2;

u₁ + v₄ = 3; 0 + v₄ = 3; v₄ = 3.

Для каждой свободной клетки найдем оценку:

∆₁₁ = u₁ + v₁ - с₁₁ = 0 - 5 - 7 = -12 < 0;

∆₁₃ = u₁ + v₃ - с₁₃ = 0 + 2 - 9 = -7 < 0;

∆₂₃ = u₂ + v₃ - с₂₃ = 7 + 2 - 8 = 1 > 0;

∆₂₄ = u₂ + v₄ - с₂₄ = 7 + 3 - 4 = 6 > 0;

∆₃₁ = u₃ + v₁ - с₃₁ = 4 - 5 - 3 = -4 < 0;

∆₃₄ = u₃ + v₄ - с₃₄ = 4 + 3 - 5 = 2 > 0.

Среди оценок есть положительные, поэтому решение не оптимально.

Этап 2. Выполним переход к новому допустимому решению.

1) Выбираем клетку (2;4), так как данная клетка имеет наибольшее положительное значение оценки ∆₂₄.

2) Для клетки (2;4) «организуем цикл»: соединим ее с помощью многоугольника с занятыми клетками: (2;2), (1;1), (1;4).

3) Расставляем в выделенных клетках «+» и «-»: в свободной клетке (2;4) «+», а в остальных по порядку «-», «+»:

	Тарифы по перемещению единицы груза, тыс.руб.
	Потребитель1	Потребитель2	Потребитель3	Потребитель4	Возможности поставщика
Поставщик1	7	4[50][+]	9	3[350][-]	400
Поставщик2	2[450]	11[100][-]	8	4[+]	550
Поставщик 3	3	8[100]	6[200]	5	300
Потребности потребителя	450	250	200	350

---

4) В клетках со знаком «-» выбираем наименьшее значение:

min (350; 100) = 100.

5) Данное наименьшее значение прибавляем в клетки со знаком «+» к объемам перевозок и вычитаем в клетках со знаком «-». Свободная клетка становится занятой, а клетка с объемом перевозок 0 – свободной.

В результате получаем новый план перевозок:

	Тарифы по перемещению единицы груза, тыс.руб.
	Потребитель1	Потребитель2	Потребитель3	Потребитель4	Возможности поставщика
Поставщик1	7	4[150]	9	3[250]	400
Поставщик2	2[450]	11	8	4[100]	550
Поставщик 3	3	8[100]	6[200]	5	300
Потребности потребителя	450	250	200	350

Матрица перевозок груза имеет вид:



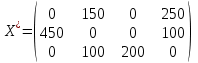
Вычислим значение целевой функции для построенного плана:



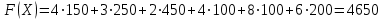
Возвращаемся к этапу 1.

Итерация 2.

Этап 1. Проверим оптимальность опорного плана.

Для занятых клеток составим систему уравнений потенциалов:

u₁ + v₂ = 4; u₁ = 0; v₂ = 4;

u₃ + v₂ = 8; 4 + u₃ = 8; u₃ = 4;

u₃ + v₃ = 6; 4 + v₃ = 6; v₃ = 2;

u₁ + v₄ = 3; 0 + v₄ = 3; v₄ = 3;

u₂ + v₄ = 4; 3 + u₂ = 4; u₂ = 1;

u₂ + v₁ = 2; 1 + v₁ = 2; v₁ = 1.

Для каждой свободной клетки найдем оценку:

∆₁₁ = u₁ + v₁ - с₁₁ = 0 + 1 - 7 = -6 < 0;

∆₁₃ = u₁ + v₃ - с₁₃ = 0 + 2 - 9 = -7 < 0;

∆₂₂ = u₂ + v₂ - с₂₂ = 1 + 4 - 11 = -6 < 0;

∆₂₃ = u₂ + v₃ - с₂₃ = 1 + 2 - 8 = -5 < 0;

∆₃₁ = u₃ + v₁ - с₃₁ = 4 + 1 - 3 = 2 > 0;

∆₃₄ = u₃ + v₄ - с₃₄ = 4 + 3 - 5 = 2 > 0.

Среди оценок есть положительные, поэтому решение не оптимально.

---

Смотрите также файлы

• Систематизация средневековой философской мысли в трудах Формы Аквинского.docx

• Химическое название.pdf

• Деятельность фирмы в условиях совершенной конкуренции.docx

• Решение задач в два действия.docx

• Наш знаменитый земляк.docx