Файл: О развитии понятия числа.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Курсовая работа

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 662

Скачиваний: 6

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

МИНИСТЕРСТВО ПРОСВЕЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное бюджетное образовательное учреждение высшего образования «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОБЛАСТНОЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»(ФГБОУ ВО «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОБЛАСТНОЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»)Физико-математический факультетКафедра высшей алгебры, математического анализа и геометрииКУРСОВАЯ РАБОТАпо учебной дисциплине «Избранные вопросы высшей математики и истории математического образования»тема: «О развитии понятия числа»Выполнил студент:группы 09.ПООБ.19.М.1 4 курсаочной формы обучения физико-математического факультетаВафина Рената Рустямовна Научный руководитель:к.п.н., доцент кафедры высшей алгебры, математического анализа и геометрииГ. В. КондратьеваДата защиты: «___» __________ 2022 г.Оценка:_____________________________________________________________(подпись научного руководителя)Регистрационный номер _________Дата регистрации:_______________Мытищи2023 Оглавление Введение 31. Развитие числа и зарождение различных систем счисления 61.1. Появления чисел 61.2. Древние ближневосточные и европейские системы счисления (вавилонская, шумерская, древнеримская, древнегреческая) 81.3. Русская, ацтекская, индийская и китайская системы счисления 102. Продолжение развития числа 132.1. Появление понятий «целого числа», «отрицательного числа» и других видов чисел 132)симметричности: ((a,b)(c,d)') ((c,d)(a,b)); 143)транзитивности: (((a,b)(c,d))h((c,d)(e,f)) ((a,b)(e, f))). 14= К ((асе + bde) + (adf + bcf), (acf + bdf) + (ade + bee)') = 16= K((ac + bd)e + (ad + bc)f, (ac + bd)f + (ad + bc)e^ = (K(a,b) ■ K(c,d)') • K(e,f), 16Определение 6.К(а, b) – К(с, d) = К(а – c,b – d). 162.2. Использование числа в развитии математических, алгебраических теорем (теорема Ролля, числа Фибоначчи и др.) 25Заключение 31Понятие числа прошло длинный исторический путь развития и наука о числах и действиях над ними необходима для прогрессивного развития человеческого общества. Числа составляют часть человеческого мышления и мы порой не отдаем себе отчета, насколько важны они в нашей жизни. 32Список использованной литературы 33 Введение Актуальность исследования истории числа обусловлена тем, что на основе требований современной действительности с ее экономическими, культурными и социальными проблемами существенно меняются основные концепции современного образования. Школе в современном обществе необходимо ориентироваться на личность обучающегося, на его всестороннее развитие. Разнообразные и сложные процессы, которые протекают в современном обществе, требуют обучать, воспитывать и развивать людей, которые будут способны к нестандартному решению проблем, то есть будут обладать творческим или, как сейчас чаще можно услышать, креативным мышлением, основными параметрами которого выступают беглость, оригинальность и гибкость мышления. Современная действительность отличается социальными, культурными и экономическими проблемами, что говорит о необходимости воспитывать и обучать в подрастающем поколении такие личности, которые будут готовы жить и работать в новых социально-экономических условиях, будут способны осуществлять непрерывное образование.На основе таких требований существенно меняются основные концепции современного образования. Школе в современном обществе необходимо ориентироваться на личность обучающегося, на его всестороннее развитие. Ученику необходимо научиться понимать и переживать все изменения, которые вокруг него происходят, чему вполне может помочь вариативное образование. Сегодня мало предоставлять ученику информацию, необходимо обучить его методам самостоятельного ее получения, необходимо научить его анализировать и прогнозировать происходящее. Для этого учащийся должен обладать развитым мышлением.Для развития математического мышления, знаний, умений и навыков в сфере математики, алгебры необходимо расширять кругозор, предлагая интеграцию учебных предметов с различными сторонами окружающей нас действительности. В последнее время задания ЕГЭ по математике содержат задачи по теории вероятностей и комбинаторике. Поэтому необходимо обучать школьников, и старшеклассников в особенности, решению таких задач. Задачи, связанные с разными системами счисления, с разными теоремами (с числами Ролля, числами Фибоначчи и др.), содержат многие популярные издания по математике, их разбирают на занятиях школьных математических кружков, они входят в комплекс заданий на математических олимпиадах.Объект исследования данной работы – исторические особенности развития чисел.Предмет исследования – анализ истории зарождения чисел, особенностей развития разных систем счисления и их роли для развития различных теорем в математической науке.Цель данной работы заключается в изучении истории развития числа во всех его видах для использования полученных результатов в проведении уроков математики.Для достижения поставленной цели необходимо решить следующие задачи:- охарактеризовать начало появления числа;- выделить древние ближневосточные и европейские системы счисления (вавилонская, шумерская, древнеримская, древнегреческая);- изучить русскую, ацтекскую, индийскую и китайскую системы счисления;- проанализировать появление понятий «целого числа», «отрицательного числа» и других видов чисел;- изучить особенности использования числа в развитии математических, алгебраических теорем (теорема Ролля, числа Фибоначчи и др.).Методы исследования данной работы были основаны на общенаучных методах анализа, синтеза, классификации, обобщения. Также были использованы хронологический, сравнительно-исторический и иные методы.Структура работы включает в себя введение, две главы, заключение, список использованных источников и литературы.  1   2   3   4

1. Развитие числа и зарождение различных систем счисления

1.1. Появления чисел

1.2. Древние ближневосточные и европейские системы счисления (вавилонская, шумерская, древнеримская, древнегреческая)

1.3. Русская, ацтекская, индийская и китайская системы счисления Развитие понятия о числе осуществлялось и в Древнем Китае. В этой стране цифры обозначались с помощью специальных иероглифов, появившихся примерно 2 тыс. лет до н. э. Однако окончательно начертание их установилось лишь к 3 веку до н. э. И сегодня применяются эти иероглифы. Сначала мультипликативным был способ записи. Число 1946, например, можно представить, используя римские цифры вместо иероглифов, как 1М9С4Х6. Но расчеты на практике производились на счетной доске, где была иной запись чисел – позиционной, как в Индии, а не десятичной, как у вавилонян. Пустым местом обозначался нуль. Лишь около 12 века н. э. появился для него специальный иероглиф.9) Многообразны и широки достижения математики в Индии. Эта страна внесла большой вклад в развитие понятия о числе. Именно здесь была изобретена десятичная позиционная система, привычная нам. Индийцы предложили символы для записи 10 цифр, с некоторыми изменениями использующиеся в наши дни повсеместно. Именно в этой стране были заложены также основы десятичной арифметики. Современные цифры произошли от индийских значков, начертание которых использовалось еще в 1 веке н. э. Изначально индийская нумерация была изысканной. Средства для записи чисел до десяти в пятидесятой степени применялись в санскрите. Сначала для цифр использовалась так называемая "сиро-финикийская" система, а с 6 века до н. э. – "брахми", с отдельными знаками для них. Эти значки, несколько видоизменившись, стали современными цифрами, называемыми сегодня арабскими. Неизвестный индийский математик примерно в 500 году н. э. изобрел новую систему записи – десятичную позиционную. Выполнение различных арифметических действий в ней было неизмеримо проще, чем в других. Индийцы в дальнейшем применяли счетные доски, которые были приспособлены к позиционной записи. Ими были разработаны алгоритмы арифметических операций, в том числе получения кубических и квадратных корней. Индийский математик Брахмагупта, живший в 7-м веке, ввел в употребление отрицательные числа. Далеко продвинулись индийцы в алгебре. Символика их более богата, чем у Диофанта, хотя несколько засорена словами. Европейские народы познакомились с ними благодаря арабам. Известный математик Леонардо Пизанский первым упоминает о них в своем основном труде “Книга Араба” изданном в 1202 году. Польша была одной из первых стран, которая ввела у себя индийскую нумерацию – произошло это в 14 веке. Арифметика, основанная на индийской нумерации, преподавалась в Польше в Краковской академии.На Руси наши предки пользовались алфавитной нумерацией, то есть числа изображались буквами, над которыми ставится значок – называемый «титло». Чтобы отделить такие буквы – числа от текста, спереди и сзади ставились точки.Этот способ обозначения цифр называется цифирью. Он был заимствован славянами от средневековых греков – византийцев. Поэтому цифры обозначались только теми буквами, для которых есть соответствия в греческом алфавите. Рисунок 1.4 – Отражение числен в системе счисления Древней РусиДля обозначения больших чисел славяне придумали свой оригинальный

2. Продолжение развития числа

2.1. Появление понятий «целого числа», «отрицательного числа» и других видов чисел

2.2. Использование числа в развитии математических, алгебраических теорем (теорема Ролля, числа Фибоначчи и др.)

Заключение

Список использованной литературы



Впервые последовательность чисел описал итальянский купец и математик Леонардо из Пизы, который был больше известен по прозвищу Фибоначчи, в своей «Книге об абаке» в 1202 г. В книге была представлена задача, при решении которой получился ряд чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597. Задача содержала вопрос: «Сколько пар кроликов в один год от одной пары рождается?» Дальше в задаче есть разъяснение, что по своей природе кролики очень быстро и продуктивно размножаются со второго месяца, как появляются на свет. Спустя месяц пара кроликов производит на свет другую пару и т. д. (рис. 1).



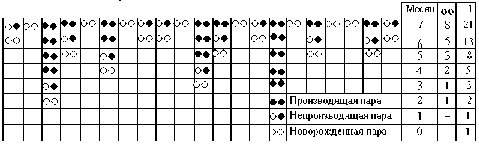
Рисунок 2.1 - Решение задачи о кроликах в виде таблицы
Что же особенного в последовательности чисел Леонардо Фибоначчи? Каждое следующее число в ряду Фибоначчи – это сумма двух предыдущих чисел. Математическим языком это записывается так: U1,U2,U3,...,Un, где Un = Un –1 + Un –2 (1)

У чисел Фибоначчи есть интересные и важные свойства. Через четыреста лет после открытия ряда чисел Фибоначчи И. Кеплером было установлено, что отношение рядом стоящих чисел с ростом n (Un + 1/Un) стремится к одному и тому же числу. Действительно,

U2/U1 = 1; U3/U2 = 2; U4/U3 = 1,5; U5/U4 = 1,66; U6 /U5 = 1,6; U7/U6 = 1,625; U8/U7 = 1,615;

U9/U8 = 1,619; U10/U9 = 1,6176; U11/U10 = 1,61818; U12/U11 = 1,61897 и т. д. (2)

Иными словами, отмечается колебание полученных отношений около постоянной величины, происходит уменьшение разницы между соседними величинами. Отношение рядом расположенных чисел Фибоначчи в пределе стремится к величине, близкой 1,618. Обозначим ее через Ф, то есть

Ф = lim Un + 1/Un = 1,618.(3)

Рассмотрим некоторые задачи, связанные с числами Фибоначчи, которые можно использовать на уроках математики в старшей школе.

Не менее интересны будут на уроках математики примеры живой природы, которые могут быть описаны с помощью последовательности Фибоначчи. Природа дает нам многочисленные примеры расположения предметов, описываемых числами Фибоначчи.

Расположение чешуек сосновых шишек: чешуйки в шишках «упакованы» по спиралям, завивающимся навстречу друг другу, причем их количество всегда выражается соседними числами Фибоначчи. В крупных шишках удается наблюдать 5 и 8 и даже 8 и 13 спиралей, на ананасе обычно их бывает 8 и 13.

Ананасовые колючки расположены в виде двух спиралей: 8 спиралей идут по ча
совой стрелке, а 13 – против часовой стрелки.

Листья на ветках деревьев расположены по спирали. Выяснилось, что в том, как листья располагаются на ветке (филлотаксис – листорасположение), количество оборотов на стебле, количество листьев в цикле – все это ряд чисел Фибоначчи. Расстояния между листьями и ветками соотносимы с числами Фибоначчи; примыкание черешков листьев к стеблю спиралевидно. Эта спираль находится между двумя соседними листьями: 1/3 полного оборота – у орешника, 2/5 – у дуба, 3/8 – у тополя и груши, 5/13 – у ивы.

Расположение семян подсолнечника. Распределение семян в корзинке также спиралевидно. Они растут по часовой и против часовой стрелки от центра корзинки (рис. 2.5). Количество этих спиралей – это два числа, идущие подряд в последовательности Фибоначчи – 21 и 34 или 34 и 55. Особенно много спиралей можно наблюдать в расположении семянок в крупных корзинках. Их число в каждом из направлений может достигать 55 и 89.


Рисунок 2.5 – Числа Фибоначчи в расположении семян подсолнечника в корзинке
Числа Фибоначчи отражают основную закономерность роста организмов, следовательно, проявляются и в строении человеческого тела.

Рассмотрим это подробнее. У человека есть части тела в единственном экземпляре: туловище, голова, сердце. Однако есть части тела, которые расположены парами: руки, ноги, глаза, почки. Ноги, руки, пальцы рук представлены тремя частями. На руках и ногах по пять пальцев, а в составе руки вместе с пальцами восемь частей.

Можно рассмотреть части тела и с другой стороны. У каждого из нас 2 руки, каждый палец, кроме большого, состоит из 3 фаланг. На каждой руке находится по 5 пальцев, только 8 пальцев трехфаланговые. Все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи.

В составе человеческого позвоночника 34 позвонка. Судя по представленному перечислению составляющих человеческого тела, при его делении на части можно проследить все числа Фибоначчи от 1 до 34.

Сложив все кости скелета, можно получить число, приближенное к 233, которое также является числом Фибоначчи.

Числа Фибоначчи можно обнаружить и в крови у человека. Если всех людей разгруппировать по трем группам крови, то получится числовое отношение 8/21/34.

Доля сокращения сердечной мышцы равна примерно 0,618 от ее изначальной длины, при нарушении этого числа при сокращении возникают заболевания сердца. А это число отражает одно из свойств чисел Фибоначчи.


В результате математической обработки экспериментальных медицинских данных, появились отношения чисел, характеризующих сердечный цикл: 0,050; 0,081; 0,131; 0,210; 0,340. Мы видим, что они отражают последовательность ряда чисел Фибоначчи 5, 8, 13, 21, 34.

В строении человеческого лица и кисти существуют и иные воплощения ряда Фибоначчи. Этот ряд получается, если провести измерения длин фаланг пальцев и расстояний между различными частями лица (рис. 6).

При помощи подобных задач учитель имеет возможность создать на уроке проблемные ситуации и активизировать самостоятельную деятельность учащихся по их разрешению, в результате чего и происходит развитие беглости и оригинальности, а значит, и креативного мышления. Для обеспечения развития беглости и оригинальности мышления учащихся необходима оптимальная последовательность ситуаций, их определенная система.



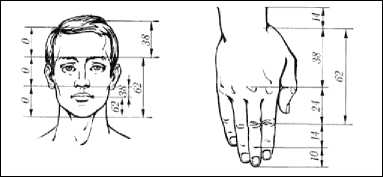
Рисунок 2.6 – Числа Фибоначчи в строении человеческого тела
Комбинаторика по своей природе является такой системой. Задачи с использованием чисел Фибоначчи помогут развить математические способности, сообразительность, укрепить память. Чтобы решать подобные задачи, учащимся потребуется проявить и волю, и упорство, и настойчивость в достижении цели, что позволит достичь высоких показателей по беглости, гибкости и оригинальности. В итоге с помощью комбинаторных задач, в том числе и с применением чисел Фибоначчи, возможно воспитать людей с высокой скоростью мыслительных операций, способных порождать разнообразные идеи, имеющие отношение к разным сферам и областям, являющиеся по своей сути интересными и необычными.



















Заключение



При исследовании истории возникновения чисел была установлена зависимость между возникновением чисел и необходимостью выражения всех чисел знаками. Эта зависимость повлияла на появление знаков-цифр, которые заменили другие не совсем удобные способы обозначения.


Понятие целого числа было известно математикам еще до нашей эры. Китайские математики использовали целые числа еще в первом веке до нашей эры. Древнегреческий математик Диофант свободно владел понятием целого числа в III веке нашей эры. Оперировали этими числами индийские математики приблизительно в 650 г. Уже в XVII веке целые числа использовались математиками в Европе, но европейские математики того времени не признавали эти числа и называли их невозможными, ложными.

Простые числа чаще встречаются в начале натурального ряда. Начало натурального ряда это три простых числа подряд 1,2,3. Переход к новому натуральному ряду зависит от личности творца. Можно стремиться к наибольшему простому числу, а можно чаще менять единицу измерения.

Впервые отрицательные числа появились в Древнем Китае приблизительно 2100 лет назад. Положительные и отрицательные числа уже умели складывать и вычитать, а правила умножения и деления не применялись. Отрицательные числа записывали черным цветом и считали «долгами», а положительные называли «имуществом» и записывали красным.

Понятие числа прошло длинный исторический путь развития и наука о числах и действиях над ними необходима для прогрессивного развития человеческого общества. Числа составляют часть человеческого мышления и мы порой не отдаем себе отчета, насколько важны они в нашей жизни.

Мы узнали о существовании различных теорий о происхождении чисел и пришли к выводу, что самым ценным вкладом в сокровищницу математических знаний человечества является употребляемый нами способ записи при помощи десяти знаков чисел: 1,2,3,4,5,6,7,8,9,0.

Система записи чисел, которой мы привыкли пользоваться в повседневной жизни, в которой производим все вычисления, на ней базируется метрическая система мер. Десятичной она называется, так как в ней используется десять различных знаков (цифры 0,1,2,3….9).

В десятичном числе 255 = 2*100+5*10+5*1 цифры «5», находящиеся на разных позициях, имеют различные количественные значения – 5 десятков и 5 единиц. При перемещении цифры на соседнюю позицию, ее «вес» изменится в 10 раз.

Арифметические действия над десятичными числами производятся с помощью достаточно простых операций, в основе которых лежат таблицы умножения и сложения, а также правило переноса: если в результате сложения двух цифр получается число, которое больше или равно 10, то оно записывается с помощью нескольких цифр, находящихся на соседних позициях.


Перевод чисел из одной системы в другую осуществляется по аналогии с предыдущими системами.

Позиционный принцип и цифровое обозначение могут быть приспособлены к системе счисления с любым основанием, кроме единицы.

Список использованной литературы





  1. Федеральный государственный образовательный стандарт среднего общего образования. Утвержден приказом Минобрнауки РФ от 17 мая 2011 г. № 413.

  2. Аристотель. Соч.: в 4 т. Т. 4. М.: Мысль, 1984.

  3. Веселовский И.Н., Белый Ю.А. Николай Коперник. М.: Наука, 1974.

  4. Виленкин Н. Я. Комбинаторика. М.: МЦНМО, 2006. 400 с.

  5. Гилфорд Дж. Три стороны интеллекта // Психология мышления. М., 1965. с. 433-456.

  6. Гуссерль Э. Начало геометрии: Введение Жака Деррида. М.: Ad Marginem, 1996.

  7. Деза Е. И., Ростовцев А. С. Модель формирования и развития математической креативности старшеклассников при обучении элементам теории специальных чисел // Modern Humanities Success / Успехи гуманитарных наук. 2019. № 4. с. 144-149.

  8. Задачник-практикум по математике. Виленкин Н.Я., М.: Просвещение, 1977.

  9. Клайн М. Математика: Утрата определенности. М.: Мир, 1984.

  10. Колесников С.А. Автор в жизни и радости... // Человек. 2018. № 5. С. 140-154.

  11. Лейбниц Г. В. Новые опыты о человеческом разуме. М.; Л: Соцэкгиз, 1936.

  12. Лейбниц Г. В. Сочинения: в 4 т. Т. 4. М.: Мысль, 1984.

  13. Лосев А.Ф. История античной эстетики: Итоги тысячелетнего развития: в 2 кн. Кн. 1. М.: Искусство, 1992.

  14. Лосев А.Ф. История античной эстетики: Итоги тысячелетнего развития: в 2 кн. Кн. 2. М.: Искусство, 1994.

  15. Лосев А.Ф. Хаос и структура. М.: Мысль, 1997.

  16. Луман Н. Истина. Знание. Наука как система. М.: Проект lettera, 2016.

  17. Майоров Г.Г. Философия как искание Абсолюта: Опыты теоретические и исторические. М.: Едиториал УРСС, 2004.

  18. Манин Ю.И. Математика как метафора. М.: МЦНМО, 2008.

  19. Математика. Учебное пособие для студентов высших педагогических учебных заведений в 2-х книгах. Г.М.Аматова, М.А.Аматов М.: Издательский центр «Академия», 2008.

  20. Математика. Упражнения и задачи. Учебное пособие для студентов высших педагогических учебных заведений. Г.М.Аматова, М.А.Аматов М.: Издательский центр «Академия», 2008. 332 с.

  21. Математика. (Для студентов I курса факультетов подготовки учителей начальных классов педагогических вузов), Столяр А.А., Лельчук М.П., Минск: «Вышэйш школа», 1976. – 272 с.

  22. Михайлов А.В. Обратный перевод. М.: Языки русской культуры, 2000.

  23. Нелюбин Л.Л., Хухуни Г.Т. История науки о языке. М.: Флинта: Наука, 2011.

  24. Платон. Собрание сочинений: в 4 т. Т. 1. М.: Мысль, 1990. (Философское наследие).

  25. Рассел Б. История западной философии. Ростов н/Д.: Миф, 1998.

  26. Ростовцев А. С. О формировании и развитии математической креативности старшеклассников с использованием многоуровневой системы математических задач // современное педагогическое образование. 2019. № 9. с. 113-117.

  27. Собрание трудов академика А.Н. Крылова: [в 12 т.] Т. 7. Ис. Ньютон «Математические начала натуральной философии». М.; Л.: Изд-во АН СССР, 1936.

  28. Сусов И.П. История языкознания. М.: Восток – Запад, 2006.

  29. Трегер Г.Ю. Эволюция основных физических идей. Киев: Наукова думка, 1989.

  30. Хомский Н. О природе и языке. С очерком: Секулярное священство и опасности, которые таит демократия / пер. с англ. П.В. Феденко. М.: URSS, 2005.

  31. Худовеков С.Н. Ориген и эллинистическое воспитание // Учен. зап. Орлов. гос. ун-та. Сер.: Гуманитарные и социальные науки. 2011. № 6. С. 318-323.

  32. Яковлев И. В. Комбинаторика для олимпиадников. М.: МЦНМО, 2016. 80 c.

  33. Яковлев В.М. О порядке чисел-символов (гуа) в мавандуйском варианте «Книги Перемен» // Разум и вера: Межвуз. сб. Петрозаводск: Изд-во Петрозаводского ун-та, 1998. С. 119-133.

Смотрите также файлы