Файл: О развитии понятия числа.docx

Введение 3

1. Развитие числа и зарождение различных систем счисления 6

1.1. Появления чисел 6

1.2. Древние ближневосточные и европейские системы счисления (вавилонская, шумерская, древнеримская, древнегреческая) 8

1.3. Русская, ацтекская, индийская и китайская системы счисления 10

2. Продолжение развития числа 13

2.1. Появление понятий «целого числа», «отрицательного числа» и других видов чисел 13

2)симметричности: ((a,b)(c,d)') ((c,d)(a,b)); 14

3)транзитивности: (((a,b)(c,d))h((c,d)(e,f)) ((a,b)(e, f))). 14

= К ((асе + bde) + (adf + bcf), (acf + bdf) + (ade + bee)') = 16

= K((ac + bd)e + (ad + bc)f, (ac + bd)f + (ad + bc)e^ = (K(a,b) ■ K(c,d)') • K(e,f), 16

Определение 6.К(а, b) – К(с, d) = К(а – c,b – d). 16

2.2. Использование числа в развитии математических, алгебраических теорем (теорема Ролля, числа Фибоначчи и др.) 25

Заключение 31

Понятие числа прошло длинный исторический путь развития и наука о числах и действиях над ними необходима для прогрессивного развития человеческого общества. Числа составляют часть человеческого мышления и мы порой не отдаем себе отчета, насколько важны они в нашей жизни. 32

Список использованной литературы 33

Введение

Актуальность исследования истории числа обусловлена тем, что на основе требований современной действительности с ее экономическими, культурными и социальными проблемами существенно меняются основные концепции современного образования. Школе в современном обществе необходимо ориентироваться на личность обучающегося, на его всестороннее развитие. Разнообразные и сложные процессы, которые протекают в современном обществе, требуют обучать, воспитывать и развивать людей, которые будут способны к нестандартному решению проблем, то есть будут обладать творческим или, как сейчас чаще можно услышать, креативным мышлением, основными параметрами которого выступают беглость, оригинальность и гибкость мышления.

Современная действительность отличается социальными, культурными и экономическими проблемами, что говорит о необходимости воспитывать и обучать в подрастающем поколении такие личности, которые будут готовы жить и работать в новых социально-экономических условиях, будут способны осуществлять непрерывное образование.

На основе таких требований существенно меняются основные концепции современного образования. Школе в современном обществе необходимо ориентироваться на личность обучающегося, на его всестороннее развитие. Ученику необходимо научиться понимать и переживать все изменения, которые вокруг него происходят, чему вполне может помочь вариативное образование. Сегодня мало предоставлять ученику информацию, необходимо обучить его методам самостоятельного ее получения, необходимо научить его анализировать и прогнозировать происходящее. Для этого учащийся должен обладать развитым мышлением.

Для развития математического мышления, знаний, умений и навыков в сфере математики, алгебры необходимо расширять кругозор, предлагая интеграцию учебных предметов с различными сторонами окружающей нас действительности. В последнее время задания ЕГЭ по математике содержат задачи по теории вероятностей и комбинаторике. Поэтому необходимо обучать школьников, и старшеклассников в особенности, решению таких задач. Задачи, связанные с разными системами счисления, с разными теоремами (с числами Ролля, числами Фибоначчи и др.), содержат многие популярные издания по математике, их разбирают на занятиях школьных математических кружков, они входят в комплекс заданий на математических олимпиадах.

Объект исследования данной работы – исторические особенности развития чисел.

Предмет исследования – анализ истории зарождения чисел, особенностей развития разных систем счисления и их роли для развития различных теорем в математической науке.

Цель данной работы заключается в изучении истории развития числа во всех его видах для использования полученных результатов в проведении уроков математики.

Для достижения поставленной цели необходимо решить следующие задачи:

- охарактеризовать начало появления числа;

- выделить древние ближневосточные и европейские системы счисления (вавилонская, шумерская, древнеримская, древнегреческая);

- изучить русскую, ацтекскую, индийскую и китайскую системы счисления;

- проанализировать появление понятий «целого числа», «отрицательного числа» и других видов чисел;

- изучить особенности использования числа в развитии математических, алгебраических теорем (теорема Ролля, числа Фибоначчи и др.).

Методы исследования данной работы были основаны на общенаучных методах анализа, синтеза, классификации, обобщения. Также были использованы хронологический, сравнительно-исторический и иные методы.

Структура работы включает в себя введение, две главы, заключение, список использованных источников и литературы.

1 2 3 4

1. Развитие числа и зарождение различных систем счисления

1.1. Появления чисел

Ученые считают, что история возникновения чисел зародилась еще в доисторические времена, когда человек научился считать предметы. Но знаки для обозначения чисел появились значительно позже: их изобрели шумеры – народ, живший в 3000–2000 гг. до н. з. в Месопотамии (ныне в Ираке).

История гласит, что на табличках из глины они выдавливали клинообразные черточки, а потом изобрели знаки. Некоторые клинописные знаки обозначали числа 1, 10, 100, то есть были цифрами, остальные числа записывались посредством соединения этих знаков. Пользование цифрами облегчало счет: считали дни недели, головы скота, размеры земельных участков, объемы урожая.

История цифр началась 5 тысячелетий назад в Египте и Месопотамии. И хотя эти два культурных пласта мало пересекались друг с другом, их системы исчисления очень похожи. Первоначально для записей использовали камень или выполняли засечки на дереве. Впоследствии в Месопотамии стали пользоваться глиняными табличками, а в Египте писали на папирусе. Внешний вид цифр в этих культурах отличается, однако одно можно сказать точно: найденные археологами артефакты подтверждают, что это были не просто записи чисел, а именно математические действия.

Искусство счета развивалось с развитием человечества. В те времена, когда человек лишь собирал в лесу плоды и охотился, ему для счета хватало четырех слов: один, два, три и много. Именно так считают сейчас некоторые племена, живущие в джунглях Южной Америки.

Количество измеряется числом, качество определяет единицу измерения количества. Определение Ньютона: «Под числом мы понимаем не столько множество, сколько отвлечённое отношение какой-нибудь величины к другой величине того же рода, принятой нами за единицу». Определим измерение как получение числового эквивалента какой-либо величины в единицах измерения. Измерение – это процесс сравнения с единицей измерения – эталоном.

Будем рассматривать натуральный ряд чисел как процесс развития чего- либо при сохранении единицы измерения. Каждый развивающийся объект должен иметь свою собственную единицу измерения, без этого невозможно установить факт развития

, так как не физически можно сравнивать только числа. В логике нет операции сравнение, в ней есть операция инверсия. Операция сравнение (вычитание) есть в арифметике. Деление тоже сравнение, но деление на нуль запрещено, поэтому будем ориентироваться на вычитание. Интуитивное сравнение будем относить к физическому посредством своего физического организма. Различные объекты могут иметь общую единицу измерения, что позволяет их сравнивать. При развитии по натуральному ряду периодически появляются простые числа. Любое простое число может стать началом нового натурального ряда, в котором все числа кратны этому простому. При разрушении единицы измерения развитие прерывается, образуется хаос. Чтобы выйти из хаоса, надо сформировать новую устойчивую единицу измерения, с которой начинается новый ряд. Новая единица формируется случайно. В природе переход к новой единице измерения при достижении простого числа случайный процесс. Возможна также остановка развития при сохранении единицы измерения.

Итак, появились числа 1, 2, 3..., которыми можно выразить количество коров в стаде, деревья в саду, волос на голове. Эти числа впоследствии получили название натуральных. Гораздо позднее появился ноль, которым обозначали отсутствие рассматриваемых предметов.

1.2. Древние ближневосточные и европейские системы счисления (вавилонская, шумерская, древнеримская, древнегреческая)

Знакомясь с числами, мы не можем не заняться знаками, с помощью которых числа обозначаются на бумаге. Знаки эти мы называем цифрами. В те времена еще не было печатных книг, но зато существовали глиняные таблички, на которых вавилонские мудрецы писали свои труды. Современные ученые нашли 44 таблички, на которых записана вся математическая наука, известная вавилонцам. Ученые Вавилона пользовались, так называемой, клинописью. Вавилонские числа являются, собственно говоря, комбинации трех клинописных знаков: единица, десятка и сотни.

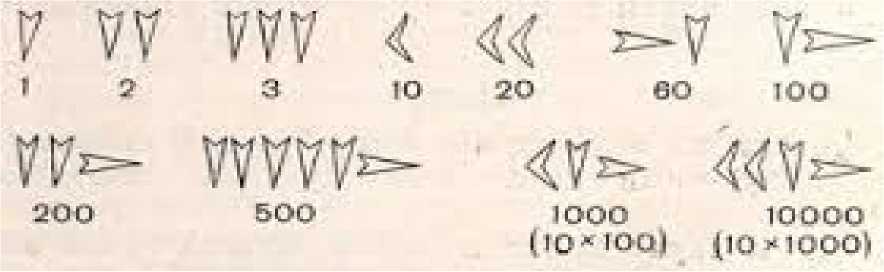
Рисунок 1.1 – Отражение чисел в системе счисления Древнего Вавилона
С помощью этих знаков можно было написать число тысяча, а также любое другое число, при этом использовались, как принцип сложения, так и умножение, а более крупные числа всегда предшествовали меньшим.

Почти столь же древними являются египетские цифры. Для выражения своих мыслей и слов на бумаге египтяне использовали знаки, которые мы в настоящее время называем иероглифами.

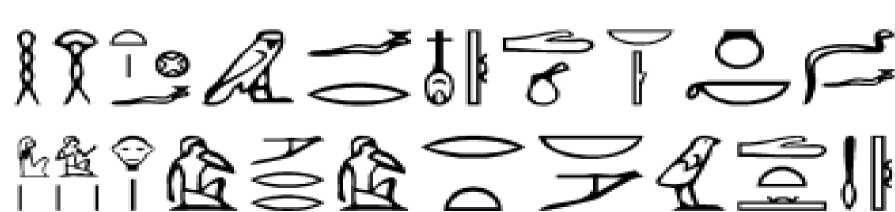
Рисунок 1.2 – Отражение чисел в системе счисления Древнего Египта

Египтяне вначале писали числа высшего порядка, а затем низшего. При этом использовался принцип сложения или умножения. Египтяне также умели пользоваться дробями. Все египетские дроби имели в числителе единицу, других дробей они не умели даже выговорить (исключение составляло 2/3). Дроби писали так же, как и натуральные числа, только над ними ставилась точка, причем для 1/2 и для 2/3 имели специальные знаки.

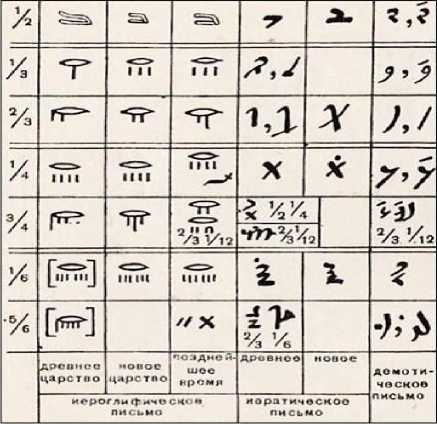
Рисунок 1.3 – Система счета Древнего Египта
Римские цифры общеизвестны и используются еще сейчас, между прочим, на циферблатах часов, надписях на мемориальных досках, при нумерации страниц книг и т.д. Известно, например, что L-это 50, С-это 100, D-это 500, M-это 1000. Знаки C и M это первые буквы слов “centum” -100 и “mille” – 1000. Знаки L и D очевидно также были первыми буквами каких-то слов, однако слова эти до нас не дошли. Можно только предполагать, что это были этрусские слова или же выражения какого-то латинского наречия. С помощью этих цифр римляне писали числа, используя правила сложения и вычитания, например, LX=60(50+10); XL=40(50-10); CM=900(1000-100); MC=1100(1000+100) и т.д. Римские цифры:

I=1 X=10 С=10^Л2 М=10^л3

V=5 L=50 D=500

Римляне пользовались дробями со знаменателями 60 (вавилонские) и со знаменателями 12, 24, 48: 1/24 – это половина, а 1/48 – это одна четвертая 1/12.

Римские ученые осваивали дроби в связи со счетом денег и использованием мер и весов. Римская монета A^ чеканенная первоначально из меди, весила 1 фунт и делилась на 12 унций. Существовало даже специальное название “deunx” для выражения 11/12 (deunx= de uncia), т.е. Ас без одной унции.

1.3. Русская, ацтекская, индийская и китайская системы счисления

Развитие понятия о числе осуществлялось и в Древнем Китае. В этой стране цифры обозначались с помощью специальных иероглифов, появившихся примерно 2 тыс. лет до н. э. Однако окончательно начертание их установилось лишь к 3 веку до н. э. И сегодня применяются эти иероглифы. Сначала мультипликативным был способ записи. Число 1946, например, можно представить, используя римские цифры вместо иероглифов, как 1М9С4Х6. Но расчеты на практике производились на счетной доске, где была иной запись чисел – позиционной, как в Индии, а не десятичной, как у вавилонян. Пустым местом обозначался нуль. Лишь около 12 века н. э. появился для него специальный иероглиф.

9) Многообразны и широки достижения математики в Индии. Эта страна внесла большой вклад в развитие понятия о числе. Именно здесь была изобретена десятичная позиционная система, привычная нам. Индийцы предложили символы для записи 10 цифр, с некоторыми изменениями использующиеся в наши дни повсеместно. Именно в этой стране были заложены также основы десятичной арифметики. Современные цифры произошли от индийских значков, начертание которых использовалось еще в 1 веке н. э. Изначально индийская нумерация была изысканной. Средства для записи чисел до десяти в пятидесятой степени применялись в санскрите. Сначала для цифр использовалась так называемая "сиро-финикийская" система, а с 6 века до н. э. – "брахми", с отдельными знаками для них. Эти значки, несколько видоизменившись, стали современными цифрами, называемыми сегодня арабскими. Неизвестный индийский математик примерно в 500 году н. э. изобрел новую систему записи – десятичную позиционную. Выполнение различных арифметических действий в ней было неизмеримо проще, чем в других. Индийцы в дальнейшем применяли счетные доски, которые были приспособлены к позиционной записи. Ими были разработаны алгоритмы арифметических операций, в том числе получения кубических и квадратных корней. Индийский математик Брахмагупта, живший в 7-м веке, ввел в употребление отрицательные числа. Далеко продвинулись индийцы в алгебре. Символика их более богата, чем у Диофанта, хотя несколько засорена словами.

Европейские народы познакомились с ними благодаря арабам. Известный математик Леонардо Пизанский первым упоминает о них в своем основном труде “Книга Араба” изданном в 1202 году. Польша была одной из первых стран, которая ввела у себя индийскую нумерацию – произошло это в 14 веке. Арифметика, основанная на индийской нумерации, преподавалась в Польше в Краковской академии.

На Руси наши предки пользовались алфавитной нумерацией, то есть числа изображались буквами, над которыми ставится значок – называемый «титло». Чтобы отделить такие буквы – числа от текста, спереди и сзади ставились точки.

Этот способ обозначения цифр называется цифирью. Он был заимствован славянами от средневековых греков – византийцев. Поэтому цифры обозначались только теми буквами, для которых есть соответствия в греческом алфавите.