Файл: О развитии понятия числа.docx

Такой способ обозначения чисел по сравнению с принятой в Европе десятичной системой был очень неудобен. Поэтому Петр 1 ввел в России привычные для нас десять цифр, отметив буквенную цифирь.

Таким образом, для отражения числа были использованы людьми в разных странах различные системы счисления.

2. Продолжение развития числа

2.1. Появление понятий «целого числа», «отрицательного числа» и других видов чисел

Понятие целого числа, операции над целыми числами, свойства этих операций имеют свою историю, используются как в математике, так и в других областях науках и техники. В математике существую задачи, являющимися неразрешимыми во множестве целых неотрицательных чисел.

Множество целых чисел получило широкое распространение спустя двадцать лет, после того, как французский математик Жирар в 1622 году указал способ геометрического изображения множества отрицательных чисел.


В математике имеется ряд задач, которые невозможно решить во множестве целых неотрицательных чисел.

Приведем пример. Решение уравнений.

Как известно, в математике множество целых неотрицательных чисел обозначается так: N₀= {0,1, 2, 3,4, 5,... }. Попробуем решить на этом множестве уравнение вида 34 + х = 5. На множестве N₀ рассматриваемое уравнение не имеет смысла, т.к. нет в данном множестве такого числа, чтобы прибавив его к числу 34 получилось бы число 5. Таким образом, уравнение вида а + х = Ьне имеет смысла на множестве N₀ при b < а [10].

Приведем другой пример. Описание процесса измерения величин.

Если некоторая величина х принимала значение а Е N₀, а потом при каком-либо процессе величина х уменьшилась на число Ь, то последнее значение можно найти по формуле у = а – Ь. Но это выражение не имеет смысла во множестве N₀, если а < Ь.

Из рассмотренных примеров следует, что их неразрешимость во множестве N₀ связана с невозможностью нахождения разности двух чисел а и Ь, где а < Ь.

Все изложенное приводит нас к тому, что необходимо построить новое множество, которое мы обозначим буквой Z. При этом множество Z должно удовлетворять следующим условиям:

• 
  множество Z включает в себя множество;
  
• 
  операции сложения, вычитания и умножения, определенные со своими свойствами во множестве N₀ также определены и для всех элементов из множества Z.
  

---

Во множестве Z любой его элемент определим как совокупность пар натуральных чисел, удовлетворяющих равенству а + d= b+ с, причем должны выполнятся условия: а > bи с > d; а < bи с < d.

Если числа хи у определяются как пары (а, b) и (с, d), то их суммой назовем следующую пару (а + c,b+ d).

Если числа хи у определяются как пары (а, b) и (с, d), то их суммой назовем следующую пару (ас + bd, ad + be).

Определение 1. Две пары натуральных чисел (а, b) и (с, d) называются эквивалентными в том и только в том случае, когда а + d= b+ с.

Эквивалентные пары обозначают так: (a, b)(c, d), причем эти пары обладают следующими свойствами:

1. 
   рефлексивности: (а,b)(b,а);
   
2. 
   симметричности: ((a,b)(c,d)') ((c,d)(a,b));
   
3. 
   транзитивности: (((a,b)(c,d))h((c,d)(e,f)) ((a,b)(e, f))).
   

Например. Докажем свойство симметричности натуральных чисел. Итак, дано (a,b)(c,d). Доказать, что из (a,b)(c,d) следует (c,d)(a,b). Действительно, из того, что выполняется (a, b')(c, d) следует а + d= b+ с, отсюда выполняется равенство b + с = а + d (по свойству коммутативности). Тогда из равенства b+ с = а + d следует равенство с + b= а + d, откуда имеем (с, d)(a, b). Что и требовалось доказать.

Аналогично доказывается и свойство транзитивности [15].

Как известно, отношение эквивалентности, заданное на множестве пар натуральных чисел, разбивает это множество на классы попарно эквивалентных пар. Обозначение К(а, Ь)означает, что это класс, которому принадлежит пара чисел (а, Ь).

Определение 2. Целым числом называется класс К(а, Ь) эквивалентных пар (а, Ь), где а,Ь Е N.

Определение 3. К(а, Ь) = К(с, d), тогда только тогда, когда (с, d)(a, b).

Определение 4. К(а, Ь) + К(с, d) = К(а + c,b+ d).

Определение 5. К(а, Ь) ■ К(с, d) = К(ас + bd, ad + be).

Из выше сказанного следует, что операции сложения и умножения целых чисел обладают следующими свойствами:

1. 
   Коммутативность сложения, т.е. К(а, Ь) + К(с, d) = К(с, d) + К(а, Ь).
   
2. 
   Ассоциативность сложения, т.е. (К(а, Ь) + К(с, d)) + К(е,/) = К(а, Ь) + (К(с, d) + K(e,f)).
   
3. 
   Коммутативность умножения, т.е. К(а, Ь) ■ К(с, d) = К(с, d) • К(а, Ь).
   
4. 
   Ассоциативность умножения, т.е. (К(а, Ь) ■ К(с, d)') • K(e,f) = К(а, b) ■ (К(с, d) ■ K(e,f)).
   
5. 
   Дистрибутивность умножения относительно сложения, т.е. (К(а, Ь) ■ (К(с, d)') + К(е, f)) = К(а, Ь) ■ К(с, d) + К(а, Ь) ■ К(е, f).
   

---

В качестве примера докажем свойство 4.

Итак, пусть дано: (К(а, Ь) ■ К(с, d)) • K(e,f), К(а, b) ■ (К(с, d) ■ K(e,f)).

Доказать: (К(а,Ь) ■ K(c,d)) • K(e,f) = К(а,Ь) ■ (K(c,d) ■ K(e,f)).

Доказательство. (К(а, b) ■ К(с, d)) • K(e,f) = К(ас + bd, ad + be) • K(e,f) = К((ас + bd)e, (ad + bc)f) = K(ace + bde, adf + bef)

К(а, b) ■ (К(с, d) ■ K(e,f)) = К(а, b) ■ K(ce + df, cf + de) = К(а(се + df), b(cf + de))

= K(ace + adf, bef + bde).

(К(а, b) ■ К(с, d)) • К(е, f) = К(а, b) ■ (К(с, d) ■ К(е, f)).

(K(a,b) ■К(c, d)) • K(e,f) = К (ас+ bd,ad + be) • K(e,f) =

= K((ac + bd)e + (ad + bc)f, (ac + bd)f + (ad + bc)e) =

K(a,b) (K (c, d) ■ K(e,f)) = К(a, b) ■ (K (ce + df, cf + de)) =

= K(a(ce + df) + b(cf + de), a(cf + de) + b(ce + df) =

= К(ace + adf + bef + bde, acf + ade + bee + bdf) =

= К ((асе + bde) + (adf + bcf), (acf + bdf) + (ade + bee)') =

= K((ac + bd)e + (ad + bc)f, (ac + bd)f + (ad + bc)e^ = (K(a,b) ■ K(c,d)') • K(e,f),

что и требовалось доказать.

Определение 6.К(а, b) – К(с, d) = К(а – c,b – d).

Определение 7. К(а, a) = 0.

Определение 8.К(а, b), где a > ^называется положительным или натуральным числом.

Определение 9.К(а, Ь), где а < ^называется отрицательным числом.

Определение 10. Если К(а, Ь) + К(с, d) = 0, то числа К(а,Ь) и K(c,d) называются противоположными целыми числами.

Определение 11. Абсолютной величиной или модулем целого числа ^называется само число х, если это число натуральное; число – х, если это число целое отрицательное и нуль при х = 0 [15].

Обозначим натуральное число К(а + п, а)через п, т.е. К(а + п,а) = п.

Свойства целых чисел:

История возникновения отрицательных чисел уходит корнями глубоко в древность. Люди очень долго не признавали их существования. Мы привыкли, что все предметы, которые нас окружают можно посчитать, а отрицательные числа являются чем-то ненастоящим.

Первое упоминание об этих числах мы находим в книге «Математика в девяти главах» китайского ученого Чжан Цаня. Эта книга является не совсем самостоятельным трудом автора, а компиляцией более ранних записей древнекитайских математиков. Здесь впервые в науке встречаются отрицательные количества, но четкого понимания сущности отрицательных величин и правил действия с ними у него нет.

---

Позднее в V-VI веках отрицательные числа начали широко использоваться в индийской математике. В то время для различных вычислений пользовались счетной доской, где числа изображались с помощью счетных палочек. Палочками красного цвета изображали положительные числа, а черным цветом – отрицательные. В Индии уже были известны правила умножения и деления, в отличие от Китая. Индийские математики пользовались отрицательными числами при решении уравнений. Они также ввели понятие «ноль» [7].

В Европе отрицательные числа тоже очень долго не признавали. Их считали «нелепыми» и просто отбрасывали при получении отрицательного ответа. И лишь в начале XIII века к идее отрицательного количества довольно близко подошел Леонардо Пизанский (Фибоначи). Он описал их в своем труде «Книга Абака» в 1202 году.

В повседневной жизни мы часто сталкиваемся с отрицательными числами. Например, если у вас на телефоне закончились деньги, но вам необходимо позвонить, то можно воспользоваться услугами связи в долг, тогда на вашем телефоне может появиться отрицательный баланс (к примеру, -25 рублей). Отрицательные числа стали неотъемлемой частью нашей жизни и мы уже не можем представить себе мир, где их нет [12].

Так, в арифметике «минус» употребляется для обозначения действия вычитания (отнять) и как знак отрицательного числа. Аналогично «плюс» обозначает действие сложения (прибавить) и знак положительного числа. И такое смешение присутствует сплошь и рядом в одних и тех же записях и вычислениях. Как же не приводит к путанице употребление одних и тех же символов для обозначения различных функций? Путаница и непонимание, конечно же, есть, но разобраться или потребовать разъяснений может только способный и настойчивый обучающийся, каких, увы, не так много.

Начнём с предположения, что знаками «плюс» и «минус» обозначаются соответственно положительные и отрицательные числа, а «прибавить» и «отнять» — за недостатком фантазии будем обозначать как «приб» и «отн». Следует заметить, что, поступив наоборот, т.е. обозначив «плюсом-минусом» действия сложения- вычитания, а как-то иначе — знаки положительных и отрицательных чисел, придём к одному и тому же результату.

Договоримся числа со своими знаками писать со скобками.

Например, вполне понятна запись: (+5) приб (+1) отн (+4) приб (-3) отн (-9).

Как должно быть известно, числа имеют «место жительства» — все они располагаются на числовой оси: положительные справа от нуля, отрицательные слева, если ось представить горизонтально с направлением вправо. Уточним слово «располагаются». Изначально число (положительное) означало длину отрезка. Числа на числовой оси — это длины отрезков, один конец которых находится в начале отсчёта. Отождествление числа с длиной отрезка было настолько наглядным и практичным средством, что от него невозможно было отказаться при появлении отрицательных чисел. Вполне естественный шаг — считать отрицательные числа тоже длинами отрезков, один конец которых также находится в начале отсчёта, но «повёрнутые» в другую сторону. Получается, таким образом, что положительные и отрицательные числа — это длины направленных отрезков: одни направлены туда же, куда и ось, другие - в противоположную сторону. Можно было бы обозначать положительные и отрицательные числа как векторы, со стрелочками: у одних чисел стрелочки направлены вправо, у других влево. Но мы будем пользоваться знаками (+) и (-). А вот складывать и вычитать будем как векторы. Для этого придадим направленным отрезкам следующее свойство: их можно перемещать вдоль числовой оси или, если угодно, отрывать от оси и снова накладывать на ось в другом месте. Естественно, при таком перемещении ни длина отрезка, ни направление не должны меняться.

---

Очевидно, что сложение двух положительных чисел равносильно нахождению длины отрезка, составленного из двух. Поэтому, когда, например, склады ваем (+5) и (+3), отрезок длиной (+3) приставляем к отрезку длиной (+5) и полу чаем отрезок длиной (+8).



Таким образом, (+5) приб (+3) = (+8).

Будем называть тот конец направленного отрезка, где нет стрелочки, началом, а со стрелочкой - просто концом направленного отрезка. Только что получилось правило сложения положительных чисел в геометрической интерпретации: прибавляя к одному числу другое, первое число-отрезок оставляем на месте, второе же число-отрезок переносим, и его начало приставляем к концу первого. В результате получаем новый направленный отрезок, у которого начало совпадает с началом первого, а конец - с концом второго. Этот направленный отрезок и будет означать сумму чисел, которые складывали.

Теперь забудем, что это правило получено для положительных чисел, и будем применять его для всех чисел. Например, к числу (-5) прибавим (-3).


Получаем: (-5) приб (-3) = (-8). Теперь к числу (-5) прибавим (+3).




Результат: (-5) приб (+3) = (-2).

Наконец, к числу (+5) прибавим число (-3).


Получим: (+5) приб (-3) = (+2).

Перейдём к следующему действию - вычитанию, которое договорились обозначать символом «отн». Используем накатанную схему: вычитая из положительных положительные же числа, выявим правило, а затем применим это правило для всех остальных случаев.

Нет ничего проще отнять из одного положительного числа другое: от отрезка «отпилить» часть, а что останется - будет результат. Правда, может оказаться, что «отпиливаемая» часть больше исходной... Значит, надо сначала рассмотреть нормальный случай: когда от большего числа вычитается меньшее.

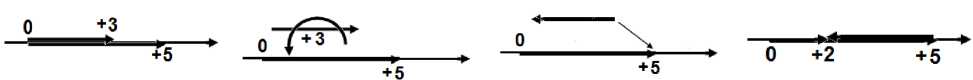Вычтем из числа (+5) число (+3). Некоторые свойства сложения мы передадим «по наследству» вычитанию, а именно: в результате должен получиться отрезок с началом в начале отсчёта, а его конец пусть упирается в конец второго отрезка (вычитаемого). Тогда для этого отрезок (+3) после отрыва от оси надо перевернуть и приставить началом в конец отрезка (+5). В результате получается отрезок (+2): (+5) отн (+3) = (+2). Поскольку в процессе переворота отрезок (+3) превращается в (-3), то действие (+5) отн. (+3) оказывается равносильным действию (+5) приб. (-3). Полученную равносильность распространим на вычитание чисел с любыми знаками и объявим правило: вычесть — это прибавить, но только число с противоположным знаком. Так (+3) отн. (+5) = (+3) приб. (-5).

---