Файл: Неравенство Чебышева.docx

Скачать файл (0,07Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 44

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

для непрерывной случайной величины

gt 

_fxe^it^xdx



является ни чем

иным как преобразованием Фурье. Отметим, что

lim gt  1.Заметим также,

t0

что можно ввести комплексную случайную величину

Z X iY, как пару

случайных величин. Очевидно, что для нее должно выполняться соотношения

MZ MX iMY, DZ  DX DY, DZ 0 .

Найдем характеристическую функцию нормального закона распределе-

ния с параметрами Тогда

m_x 0 ,

_x 1,

fx

1 ^^x2

2



e ,

2

_

 _x²_

_ACB²__t²

gt 

__e₂_eitx_d_x_^__eAx²2 BxC_d_x_

 _

e ^A^ e ².



_
Исходя из определения характеристической функции, перечислим ее

основные свойства:

- lim gt  1;

t0

-если y ax, то g_yt  g_xat;

n n

-если

x_iнезависимые и

Y _x_i, то

1

g_yt  _g_xt.

1

Далее, используем первое свойство

t 0:

gt, разложим ее в ряд Маклорена при

gt  g0  g^0 t g^0 t²  ,

где

g_x0 1,

x x

g^_x0  im_x 0 ,

x

g^_x0  

x

x
² . Тогда

g_xt  1

_2

_x_t2 _.

2

Используем третье свойство

gt. Для суммы случайных величин Yха-

рактеристическая функция будет иметь вид

gt  gtⁿ. Получаем в преде-

y x
  n

 ² n

_2_t2


ле n,

g_yt 

_1 



2

x_t2

2 _

 _1 



y_t₂_

2n _

_y

 e ²
__t2

. Если обезразмерить слу-

чайную величину Y,

Z y _y

то g_Zt  e ².

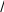Таким образом, сумма случайных величин но, распределена по нормальному закону.

Примеры

x_iпри

n, действитель-

Складываются 24 независимых случайных величины, равномерно рас- пределенных в интервале 0,1. Написать приближенное выражение плотности

распределения суммы этих случайных величин. Найти так же вероятность того, что сумма будет заключена в пределах от 6 до 8.


24

Решение: Y

1

x_i, где

fx  ^^1,

^0,


0  x 1

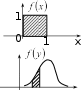x 0,x 1

_m_0  1 _1 _,

D ¹, m nP12 , D nD

 2 .

^x2 2

x ₁₂y y x

Используем центральную предельную теорему

n  20:

fy

₁_ y12²



4

e

4
6 12 y

P6  Y 8  Ф^⁸^¹²^ Ф^⁶^¹²^ Ф2,8  Ф4,2  0,005 .

   

   

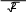
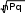Автомат изготавливает 80% изделий первого сорта и 20% второго сор- та. Найти вероятность, что среди наудачу выбранных 10000 изделий окажется от 7960 до 8040 изделий первого сорта.

Решение.

P 0,8,

q 0,2 ,

m_y nP 8000 ,

 _y

 40 .

Применим теорему Муавра-Лапласса

P7960  Y 8040  2Ф1  0,68.

Сто бомбардировщиков независимо производят серийное бомбомета- ние по полосе укреплений. Каждый из бомбардировщиков сбрасывает серию

бомб. Для одной серии

m 2

бомбы и

 1

бомба. Найти вероятность попа-

дания в полосу укреплений от 170 до 230 бомб.

Решение.

m_y100m 200,

 _y

n  10









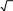P170  Y 230  Ф^²³⁰^²⁰⁰^ Ф^¹⁷⁰^²⁰⁰^ 2Ф3  0,997 .

 ₁₀  ₁₀

В процессе производства 60% изделий получается высшего сорта. Наудачу отбирают 200 изделий. Найти вероятность, что среди отобранных из- делий от 120 до 150 являются изделиями высшего сорта.

Решение.

P 0,6 ,

q 0,4 ,

m_y np 120 ,. D_y

 npq 48 ,

 _y 7

P120  Y 150  Ф^¹⁵⁰^¹²⁰

Смотрите также файлы

Протокол от 2022 г. Руководитель (Дутова О. В.) Согласовано на заседании мс.docx

Курсовая работа (курсовой проект) по учебному курсу Электроснабжение Вариант 13. 17 (при наличии) Студент.docx

К 70летию Победы в Великой Отечественной войне посвящается Вклад ученых физиков Осетии в дело Великой Победы.docx

План работы по обеспечению здоровьесберегающей среды Цель.docx

Сервисная деятельность.docx

Файл: Неравенство Чебышева.docx

Примеры

Смотрите также файлы

Информация

Списки файлов

Дополнительно