Дисперсии и среднеквадратические отклонения.

Признаки x и y
Для y и x1	3600	314.286	60	17.728
Для y и x2	5913.265	314.286	76.898	17.728
Для y и x3	77.837	314.286	8.823	17.728
Для x1 и x2	5913.265	3600	76.898	60
Для x1 и x3	77.837	3600	8.823	60
Для x2 и x3	77.837	5913.265	8.823	76.898

Матрица парных коэффициентов корреляции R:

-	y	x1	x2	x3
y	1	-0.7158	0.5365	0.9335
x1	-0.7158	1	-0.8855	-0.5451
x2	0.5365	-0.8855	1	0.449
x3	0.9335	-0.5451	0.449	1

Частные коэффициенты корреляции.

---

Коэффициент частной корреляции отличается от простого коэффициента линейной парной корреляции тем, что он измеряет парную корреляцию соответствующих признаков (y и x_i) при условии, что влияние на них остальных факторов (x_j) устранено.

На основании частных коэффициентов можно сделать вывод об обоснованности включения переменных в регрессионную модель. Если значение коэффициента мало или он незначим, то это означает, что связь между данным фактором и результативной переменной либо очень слаба, либо вовсе отсутствует, поэтому фактор можно исключить из модели.

Частные коэффициенты корреляции вычисляются по формуле:



где R_ij - алгебраическое дополнение элемента r_ij матрицы R.



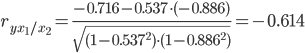
Теснота связи умеренная.



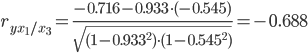
Теснота связи умеренная.



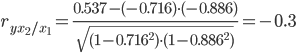
Теснота связи не сильная.



Теснота связи не сильная.



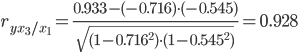
Теснота связи весьма сильная.



Теснота связи весьма сильная.





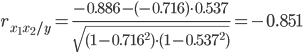
Теснота связи сильная.



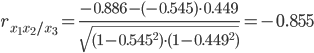
Теснота связи сильная.

---

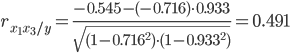
Теснота связи не сильная.



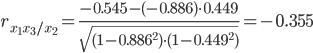
Теснота связи не сильная.





Теснота связи низкая. Межфакторная связь слабая.



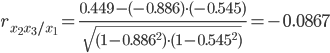
Теснота связи низкая. Межфакторная связь слабая.

При сравнении коэффициентов парной и частной корреляции видно, что из-за влияния межфакторной зависимости между x_i происходит завышение оценки тесноты связи между переменными.

Анализ мультиколлинеарности.

Если факторные переменные связаны строгой функциональной зависимостью, то говорят о полной мультиколлинеарности. В этом случае среди столбцов матрицы факторных переменных Х имеются линейно зависимые столбцы, и, по свойству определителей матрицы, det(X^TX = 0).

Вид мультиколлинеарности, при котором факторные переменные связаны некоторой стохастической зависимостью, называется частичной. Если между факторными переменными имеется высокая степень корреляции, то матрица (X^TX) близка к вырожденной, т. е. det(X^TX ≧ 0) (чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии).

1. Анализ мультиколлинеарности на основе матрицы коэффициентов корреляции.

Если в матрице есть межфакторный коэффициент корреляции r_xjxi>0.7, то в данной модели множественной регрессии существует мультиколлинеарность.

В нашем случае r(x₁x₂) имеют |r|>0.7, что говорит о мультиколлинеарности факторов и о необходимости исключения одного из них из дальнейшего анализа.

2. Ридж-регрессия.

Наиболее детальным показателем наличия проблем, связанных с мультиколлинеарностью, является коэффициент увеличения дисперсии, определяемый для каждой переменной как:

---

где R_j² коэффициент множественной детерминации в регрессии X_j на прочие X.

О мультиколлинеарности будет свидетельствовать VIF от 4 и выше хотя бы для одного j.

VIF(b_1,2)=

Поскольку VIF ≥ 4, что говорит о мультиколлинеарности факторов x₁, x₂ и о необходимости исключения одного из них из дальнейшего анализа.

VIF(b_1,3)=

VIF(b_2,3)=

3. Критерием плохой обсуловленности является высокая величина отношения λ_max/λ_min максимального и минимального собственных чисел матрицы X^TX — называемого показателем обусловленности. Это соотношение также позволяет судить о степени серьезности проблем мультиколлинеарности: показатель обусловленности в пределах от 10 до 100 свидетельствует об умеренной коллинеарности, свыше 1000 — об очень серьезной коллинеарности.

Модель регрессии в стандартном масштабе.

Модель регрессии в стандартном масштабе предполагает, что все значения исследуемых признаков переводятся в стандарты (стандартизованные значения) по формулам:



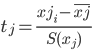
где х_ji - значение переменной х_ji в i-ом наблюдении.



Таким образом, начало отсчета каждой стандартизованной переменной совмещается с ее средним значением, а в качестве единицы изменения принимается ее среднее квадратическое отклонение S.

Если связь между переменными в естественном масштабе линейная, то изменение начала отсчета и единицы измерения этого свойства не нарушат, так что и стандартизованные переменные будут связаны линейным соотношением:

---

t_y = ∑β_jt_xj

Для оценки β-коэффициентов применим МНК. При этом система нормальных уравнений будет иметь вид:

r_x1y=β₁+r_x1x2•β₂ + ... + r_x1xm•β_m

r_x2y=r_x2x1•β₁ + β₂ + ... + r_x2xm•β_m

r_xmy=r_xmx1•β₁ + r_xmx2•β₂ + ... + β_m

Для наших данных (берем из матрицы парных коэффициентов корреляции):

-0.716 = β₁ -0.886β₂ -0.545β₃

0.537 = -0.886β₁ + β₂ + 0.449β₃

0.933 = -0.545β₁ + 0.449β₂ + β₃

Данную систему линейных уравнений решаем методом Гаусса: β₁ = -0.598; β₂ = -0.333; β₃ = 0.757;

Стандартизированная форма уравнения регрессии имеет вид:

t_y = -0.598x₁ -0.333x₂ + 0.757x₃

Найденные из данной системы β–коэффициенты позволяют определить значения коэффициентов в регрессии в естественном масштабе по формулам:

---

Смотрите также файлы

• Электроэнергетика мира Учитель Ерофеева Наталья Николаевна моу Лицей 26 Цель урока.doc

• Курсовая работа Игра Точки и квадраты.docx

• Тема проекта (работы).docx

• Премии в области качества.docx

• Сценарий занятия ( проводится в 1 занятие, для учащихся 9 11 классов.).docx