ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 35
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
a = y - ∑bj·xj
3. Анализ параметров уравнения регрессии.
Перейдем к статистическому анализу полученного уравнения регрессии: проверке значимости уравнения и его коэффициентов, исследованию абсолютных и относительных ошибок аппроксимации
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка ε = Y - Y(x) = Y - X*s (абсолютная ошибка аппроксимации)
| Y | Y(x) | ε = Y - Y(x) | ε2 | (Y-Yср)2 | |ε : Y| |
| 229 | 230.527 | -1.527 | 2.332 | 289 | 0.00667 |
| 230 | 230.45 | -0.45 | 0.203 | 324 | 0.00196 |
| 217 | 219.767 | -2.767 | 7.657 | 25 | 0.0128 |
| 207 | 199.214 | 7.786 | 60.619 | 25 | 0.0376 |
| 216 | 213.714 | 2.286 | 5.224 | 16 | 0.0106 |
| 212 | 212.853 | -0.853 | 0.728 | 0 | 0.00402 |
| 173 | 177.474 | -4.474 | 20.013 | 1521 | 0.0259 |
| | | | 96.777 | 2200 | 0.0995 |
Средняя ошибка аппроксимации
Оценка дисперсии равна:
se2=(Y-Y(X))T(Y-Y(X))=96.777
Несмещенная оценка дисперсии равна:
Оценка среднеквадратичного отклонения (стандартная ошибка для оценки Y):
Найдем оценку ковариационной матрицы вектора k = S2 • (XTX)-1
| k(x) = 32.26 |
| = |
|
Дисперсии параметров модели определяются соотношением S2i = Kii, т.е. это элементы, лежащие на главной диагонали
Sb0=
Sb1=
Sb2=
Sb3=
Показатели тесноты связи факторов с результатом.
Если факторные признаки различны по своей сущности и (или) имеют различные единицы измерения, то коэффициенты регрессии bj при разных факторах являются несопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с результатом, позволяющими ранжировать факторы по силе влияния на результат.
К таким показателям тесноты связи относят: частные коэффициенты эластичности, β–коэффициенты, частные коэффициенты корреляции.
Частные коэффициенты эластичности.
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле:
Частный коэффициент эластичности показывает, насколько процентов в среднем изменяется признак-результат у с увеличением признака-фактора хj на 1% от своего среднего уровня при фиксированном положении других факторов модели.
E1=
При изменении фактора х1 на 1%, Y изменится на -0.533%. Частный коэффициент эластичности |E1| < 1. Следовательно, его влияние на результативный признак Y незначительно.
E2=
При изменении фактора х2 на 1%, Y изменится на -0.0261%. Частный коэффициент эластичности |E2| < 1. Следовательно, его влияние на результативный признак Y незначительно.
E3=
При изменении фактора х3 на 1%, Y изменится на 1.613%. Частные коэффициент эластичности |E3| > 1. Следовательно, он существенно влияет на результативный признак Y.
Стандартизированные частные коэффициенты регрессии.
Стандартизированные частные коэффициенты регрессии - β-коэффициенты (βj) показывают, на какую часть своего среднего квадратического отклонения S(у) изменится признак-результат y с изменением соответствующего фактора хj на величину своего среднего квадратического отклонения (Sхj) при неизменном влиянии прочих факторов (входящих в уравнение).
По максимальному βj можно судить, какой фактор сильнее влияет на результат Y.
По коэффициентам эластичности и β-коэффициентам могут быть сделаны противоположные выводы. Причины этого: а) вариация одного фактора очень велика; б) разнонаправленное воздействие факторов на результат.
Коэффициент βj может также интерпретироваться как показатель прямого (непосредственного) влияния j-ого фактора (xj) на результат (y). Во множественной регрессии j-ый фактор оказывает не только прямое, но и косвенное (опосредованное) влияние на результат (т.е. влияние через другие факторы модели).
Косвенное влияние измеряется величиной: ∑βirxj,xi, где m - число факторов в модели. Полное влияние j-ого фактора на результат равное сумме прямого и косвенного влияний измеряет коэффициент линейной парной корреляции данного фактора и результата - rxj,y.
Так для нашего примера непосредственное влияние фактора x1 на результат Y в уравнении регрессии измеряется βj и составляет -0.598; косвенное (опосредованное) влияние данного фактора на результат определяется как:
rx1x2β2 = -0.886 * (-0.333) = 0.2946
Сравнительная оценка влияния анализируемых факторов на результативный признак.
5. Сравнительная оценка влияния анализируемых факторов на результативный признак производится:
- средним коэффициентом эластичности, показывающим на сколько процентов среднем по совокупности изменится результат y от своей средней величины при изменении фактора x
i на 1% от своего среднего значения;
- β–коэффициенты, показывающие, что, если величина фактора изменится на одно среднеквадратическое отклонение Sxi, то значение результативного признака изменится в среднем на β своего среднеквадратического отклонения;
- долю каждого фактора в общей вариации результативного признака определяют коэффициенты раздельной детерминации (отдельного определения): d2i = ryxiβi.
d21 = -0.72*(-0.598) = 0.428
d22 = 0.54*(-0.333) = -0.178
d23 = 0.93*0.757 = 0.707
При этом должно выполняться равенство:
∑di2 = R2 = 0.956
Множественный коэффициент корреляции (Индекс множественной корреляции).
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции.
В отличии от парного коэффициента корреляции, который может принимать отрицательные значения, он принимает значения от 0 до 1.
Поэтому R не может быть использован для интерпретации направления связи. Чем плотнее фактические значения yi располагаются относительно линии регрессии, тем меньше остаточная дисперсия и, следовательно, больше величина Ry(x1,...,xm).
Таким образом, при значении R близком к 1, уравнение регрессии лучше описывает фактические данные и факторы сильнее влияют на результат. При значении R близком к 0 уравнение регрессии плохо описывает фактические данные и факторы оказывают слабое воздействие на результат.
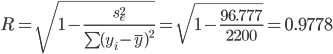
Коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции:
где Δr - определитель матрицы парных коэффициентов корреляции; Δr11 - определитель матрицы межфакторной корреляции.
| Δr = |
| = 0.00662 |