Файл: Методические указания по проведению практических занятий по метрологии и измерительной технике для студентов всех специальностей очной формы обучения.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 259
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, где 
класс точности, а 
конечное значение шкалы (предел измерения см. табл. 3.1 [4] ).Следовательно:
(А);
(А);
(А).Ответ:
Большую точность измерения тока обеспечит второй амперметр.
Задача № 2.14
Можно ли определить величину измеряемого напряжения, если известно, что оно измерено с относительной погрешностью
% прибором с пределом измерения 
В, а класс точности имеет на шкале условное обозначение вида 
?Решение:
При таком условном обозначении класса точности относительная погрешность результата измерения определяется выражением (см. табл. 3.1 [4]):
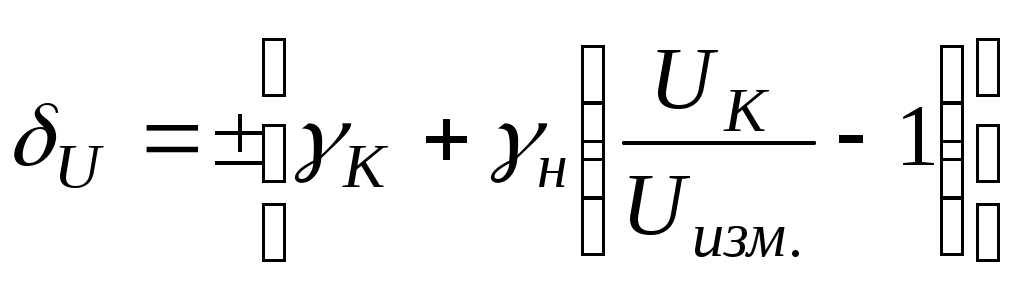%.Следовательно, можем записать:
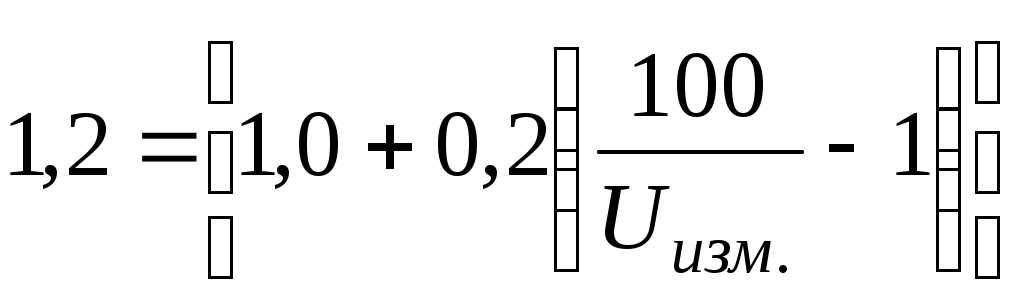, откуда 
В.Ответ: Можно,
В.Задача № 2.15
Необходимо выполнить однократное измерение падения напряжения на участке цепи с погрешностью, не превышающей
%.Априорные данные об исследуемом объекте и условиях проведения измерительного эксперимента:
Участок цепи представляет собой стабильное сопротивление
Ом;
Ток в цепи постоянный;
Измерение проводится в сухом отапливаемом помещении при температуре до +30С и напряженности внешнего магнитного поля до 300 А/м;
Предполагаемое падение напряжения на участке цепи постоянно и не превышает 1,5 В.
Для измерений выбран вольтметр класса точности 0,5 с верхним пределом измерения
В. Показания вольтметра при измерении 
В. При изучении метрологических характеристик вольтметра по техническому описанию установлено, что:
Внутреннее сопротивление вольтметра
Ом, 
%.Нормальные условия эксплуатации следующие:
температура окружающего воздуха
С;напряженность внешнего магнитного поля
А/м;дополнительная температурная погрешность не превышает основной, при отклонении температуры от нормальной на каждые 10С;
дополнительная погрешность, обусловленная отклонением внешнего магнитного поля от нормальной не превышает половины основной, при отклонении напряженности внешнего магнитного поля от нормальной на каждые 100 А/м.
Решение:
1. Известно, что при измерении напряжения методическая погрешность определяется соотношением между сопротивлением участка цепи
и сопротивлением вольтметра 
. Методическая погрешность в относительной форме определяется соотношением
%.Очевидно, что если напряжение должно быть измерено с погрешностью не более
%, то в результат измерения необходимо внести поправку на методическую погрешность.Величина поправки в абсолютной форме определяется по формуле
(В).Тогда с учетом поправки результат измерения будет
(В).Поскольку
и 
известны с погрешностями, то введением поправки не удается полностью исключить методическую погрешность, неисключенный остаток методической погрешности определяется погрешностями 
% и 
%. Границы неисключенного остатка методической погрешности можно оценить, зная что:
; %; %.Оценка границ неисключенного остатка методической погрешности дает результат
%. (Оценка границ неисключенного остатка методической погрешности в данной задаче не рассматривается, так как для этого необходимо воспользоваться правилами определения погрешности результата косвенных измерений. Определение границ неисключенного остатка методической погрешности приводится в решении задачи № 2.17).2. Определяем границы основной погрешности результата измерения
%.3. Определяем границы дополнительной температурной погрешности
%.4. Определяем границы дополнительной погрешности от влияния внешнего магнитного поля
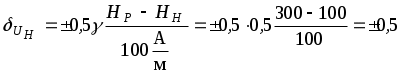%.5. Сравнивая границы неисключенного остатка методической погрешности
с границами основной и дополнительных погрешностей, делаем вывод, что величина пренебрежимо мала, по сравнению с другими погрешностями и
ее можно не учитывать. Принимая во внимание, что все составляющие погрешности измерения напряжения получены через класс точности вольтметра в виде границ, а о виде закона распределения каждой из составляющих достоверных сведений нет, границы погрешности результата находим по формуле (2.35 [4] ), задав доверительную вероятность
и записав формулу для относительных погрешностей в виде:
%.Учитывая, что число составляющих погрешности мало, оценим арифметическую сумму их
%.Так как
, то в качестве границ погрешности результата измерения принимаем доверительные границы при .6. Доверительные границы в абсолютной форме
(В).Следовательно, результат измерения в окончательном виде можно представить в форме:
В; 
В; 
или
В; .Ответ:
В; .Задача № 2.16
Мощность Р, потребляемая нагрузкой с сопротивлением
, измеряется косвенным методом и вычисляется в соответствии с формулой
.
Оценки значения тока и величины сопротивления нагрузки
и 
по условиям эксперимента могут быть получены путем прямых однократных измерений с относительными погрешностями, пределы которых оцениваются величинами: 
% и 
% соответственно. Определить пределы относительной погрешности, с которой в этих условиях будет измерена мощность потребляемая нагрузкой.Решение:
В соответствии с изложенным выше, измерение мощности представляет собой обыкновенное нелинейное косвенное измерение. Оценку результата измерения в соответствии с (3.11 [4]) можем записать:
,где
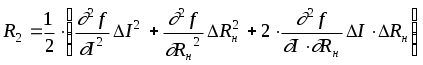остаточный член разложения исходной функции в ряд Тейлора;
; 
; 
; 
; 
.Убедимся в возможности линеаризации исходного уравнения, для чего оценим величину остаточного члена
. Так как по условию задачи сами оценки значения аргументов и остаются неизвестными, перейдем к относительной форме выражения погрешностей.
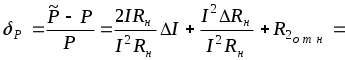
,где :
