Файл: Методические указания по проведению практических занятий по метрологии и измерительной технике для студентов всех специальностей очной формы обучения.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 261
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Оценим величину остаточного члена по сравнению с другими погрешностями. Очевидно, что
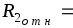
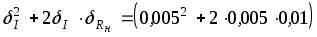
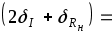
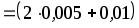 .
.
Следовательно, линеаризация исходного уравнения правомерна и остаточным членом разложения можно пренебречь, при этом получаем
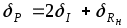 .
.
Принимая во внимание тот факт, что значения аргументов по условию задачи измерялись путем обыкновенных однократных прямых измерений, следует считать, что пределы относительных погрешностей аргументов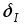 и
и 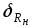 определены с использованием информации о классе точности используемых приборов.
определены с использованием информации о классе точности используемых приборов.
Следовательно, для определения пределов относительной погрешности измерения мощности следует воспользоваться формулой (2.35 [4] ), записав ее для относительных погрешностей:
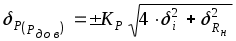 .
.
Приняв доверительную вероятность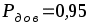 , получаем
, получаем
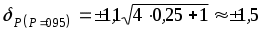 %.
%.
Учитывая, что суммируются всего две составляющие погрешности, оценим их арифметическую сумму
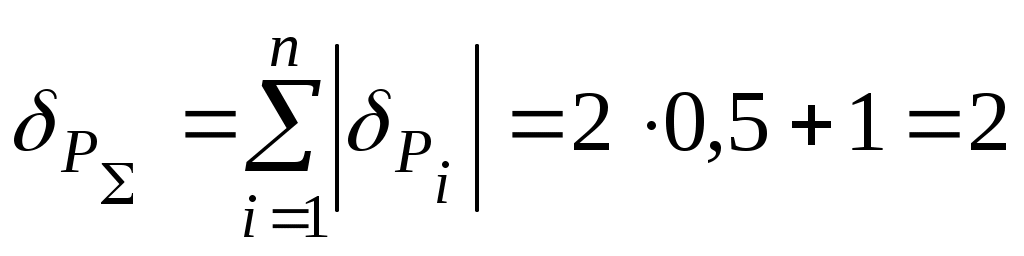 %.
%.
Так как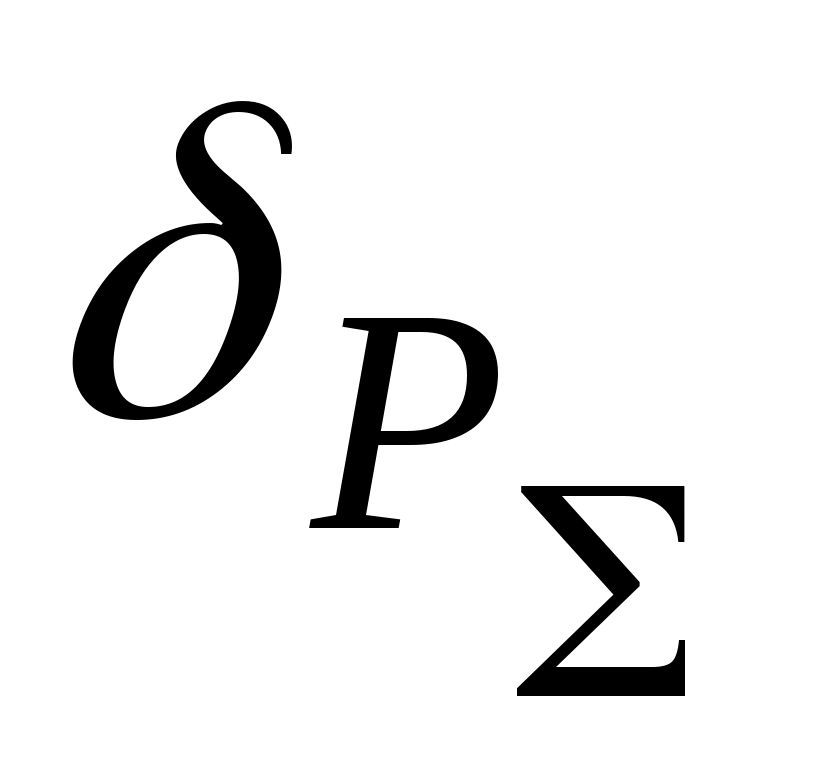
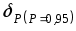 , то в качестве границ погрешности результата измерения мощности принимаем доверительные границы при
, то в качестве границ погрешности результата измерения мощности принимаем доверительные границы при 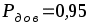 .
.
Ответ: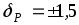 %,
%, 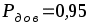 .
.
Задача № 2.17
Оценить границы неисключенного остатка методической погрешности измерения напряжения по условиям задачи № 2.15.
Решение:
Абсолютное значение методической погрешности определяется формулой (см. задачу № 2.15)
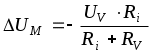 .
.
Вычислить точное значение поправки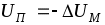 невозможно, поскольку значения резисторов
невозможно, поскольку значения резисторов  и
и  известны с погрешностями (показания вольтметра
известны с погрешностями (показания вольтметра 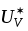 , для которого определяется поправка, считаются const). Оценка абсолютного значения поправки дана в задаче № 2.15
, для которого определяется поправка, считаются const). Оценка абсолютного значения поправки дана в задаче № 2.15
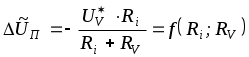 .
.
Учитывая, что функция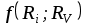 достаточно проста, а погрешности аргументов малы
достаточно проста, а погрешности аргументов малы 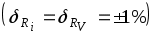 считаем, что линеаризация исходной функции правомерна. Границы абсолютной погрешности определения величины поправки найдем, воспользовавшись формулой (3.14 [4] ).
считаем, что линеаризация исходной функции правомерна. Границы абсолютной погрешности определения величины поправки найдем, воспользовавшись формулой (3.14 [4] ).
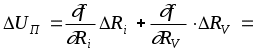
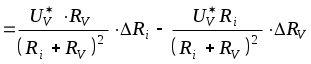 .
.
Погрешности аргументов известны в виде границ, т. к. о законе распределения ничего не известно, определяем границы погрешности результата по формуле (2.35) с учетом (3.14). Принимая во внимание тот факт, что приходится суммировать всего две составляющих, оценим максимально возможные границы погрешности определения поправки
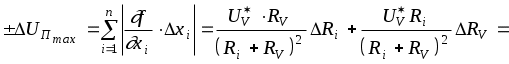
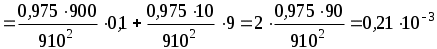 (В).
(В).
Таким образом, границы неисключенного остатка методической погрешности в абсолютной форме
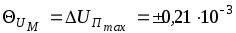 В.
В.
Границы неисключенного остатка методической погрешности в относительной форме
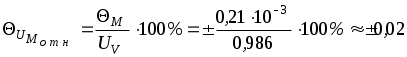
%.
Ответ: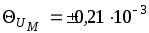 В;
В; 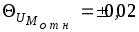 %.
%.
Задача № 2.18
Обработать результаты многократных прямых измерений тока, проведенных одним и тем же прибором за достаточно малый промежуток времени. При измерении получены следующие результаты (в мА):
10,07; 10,10; 10,15; 10,16; 10,17;
10,20; 10,40; 10,13; 10,12; 10,08.
Считать, что полученная совокупность результатов свободна от систематических погрешностей и подчиняется нормальному закону распределения.
Решение:
Из условия задачи следует, что полученная совокупность результатов представляет собой выборку равноточных нормально распределенных данных. Используя формулы раздела 2.3 [4], получаем:
1) Наиболее вероятное значение измеренной величины (оценка действительного значения тока)
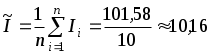 (мА);
(мА);
2) Оценка средней квадратичной погрешности (СКП) экспериментальных данных
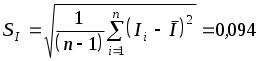 (мА);
(мА);
3) В полученной совокупности экспериментальных данных седьмой результат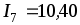 мА существенно отличается от остальных. Проверим, не содержит ли он грубую погрешность?
мА существенно отличается от остальных. Проверим, не содержит ли он грубую погрешность?
Определим
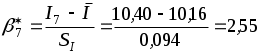 .
.
Зададим доверительную вероятность и по таблице №3 Приложения находим допускаемую величину
и по таблице №3 Приложения находим допускаемую величину 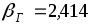 для выборки из 10 результатов при
для выборки из 10 результатов при  .
.
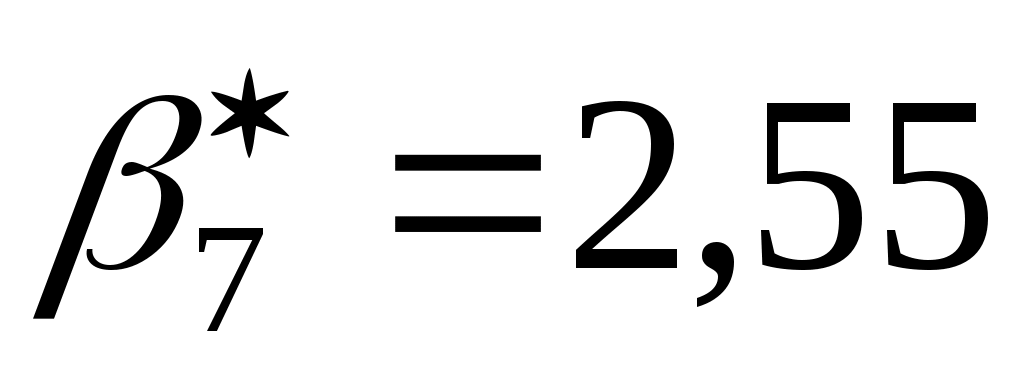
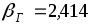 ,
,
следовательно, результат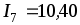 мА содержит грубую погрешность и должен быть отброшен. Количество результатов в выборке уменьшается до
мА содержит грубую погрешность и должен быть отброшен. Количество результатов в выборке уменьшается до 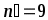
.
4) Уточняем значения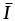 и
и 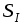
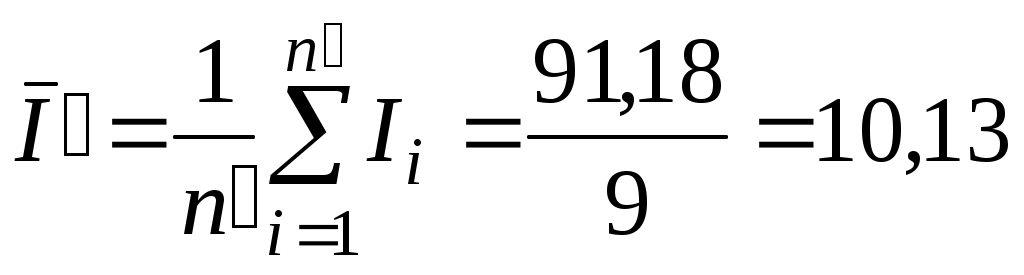 (мА)
(мА)
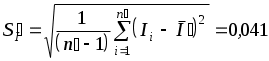 (мА).
(мА).
В оставшейся совокупности результатов следует проверить еще результат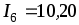 мА. При той же доверительной вероятности
мА. При той же доверительной вероятности  для выборки из 9 результатов находим табличное значение
для выборки из 9 результатов находим табличное значение 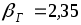 . Определяем
. Определяем 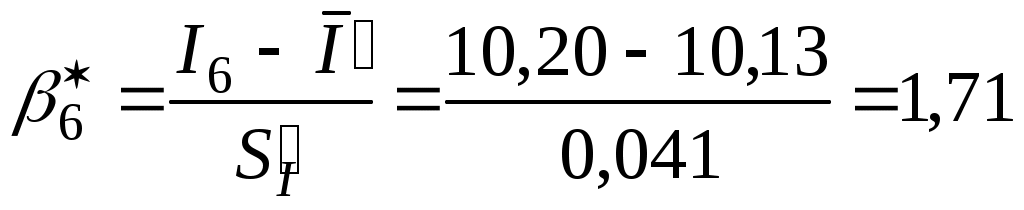 .
.
Так как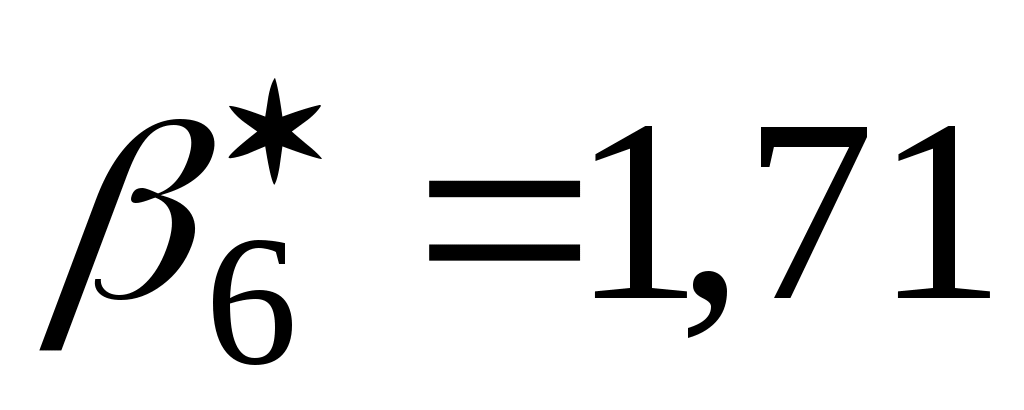
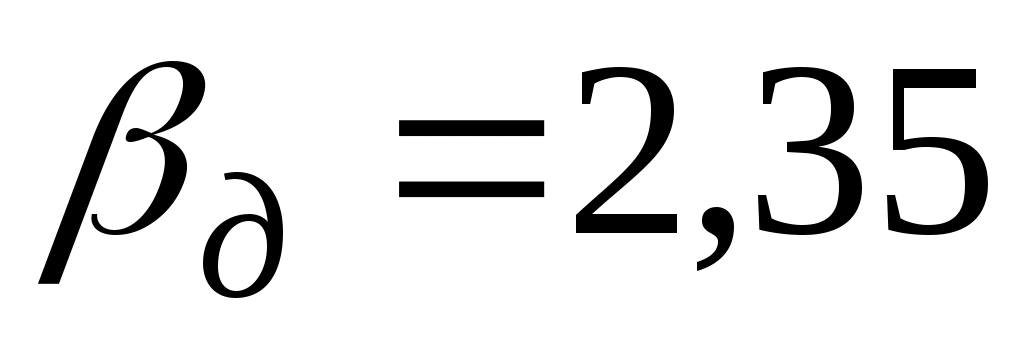 , результат измерения
, результат измерения 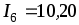 мА должен быть оставлен.
мА должен быть оставлен.
5) Определим СКП результата измерения (за результат измерения принимается уточненное значение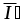 )
)
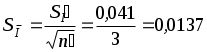 (мА).
(мА).
6) Определим границы доверительного интервала для результата измерений. Так как число обрабатываемых результатов 20, то при определении коэффициента
20, то при определении коэффициента 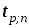 пользуемся табличными значениями распределения Стьюдента (см. Приложение). Задаем доверительную вероятность
пользуемся табличными значениями распределения Стьюдента (см. Приложение). Задаем доверительную вероятность  и для выборки из 9 наблюдений находим
и для выборки из 9 наблюдений находим 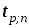 = 2,31.
= 2,31.
Границы доверительного интервала для результата измерения
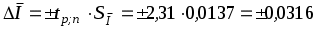 (мА).
(мА).
7) Запишем результат измерения с указанием доверительной погрешности (соблюдая все правила метрологии при округлении значения погрешности и значения результата при окончательной записи результата измерений).
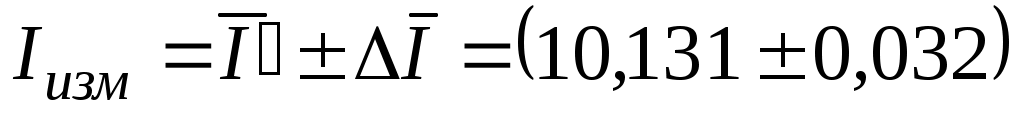 мА;
мА;  ;
; 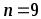 ,
,
или 10,099 мА 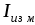 10,163 мА;
10,163 мА;  ;
; 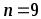 .
.
Ответ: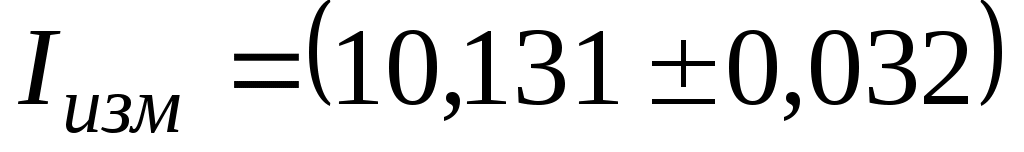 мА;
мА;  ;
; 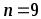 ,
,
или 10,099 мА 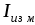 10,163 мА;
10,163 мА;  ;
; 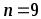 .
.
Примечание: обе записи результата соответствуют требованиям стандарта и являются равнозначными.
Задача № 2.19
Для выяснения закона распределения случайных отклонений изготовленных резисторов от номинала было проведено измерение точного значения 200 резисторов из одной партии. Номинальное значение резисторов 300 Ом. В результате предварительной обработки результатов измерений получены следующие данные:
Максимальное значение резистора в выборке -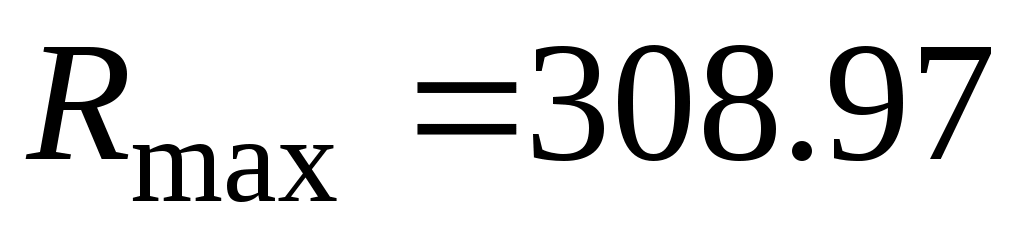 Ом;
Ом;
Минимальное значение резистора в выборке -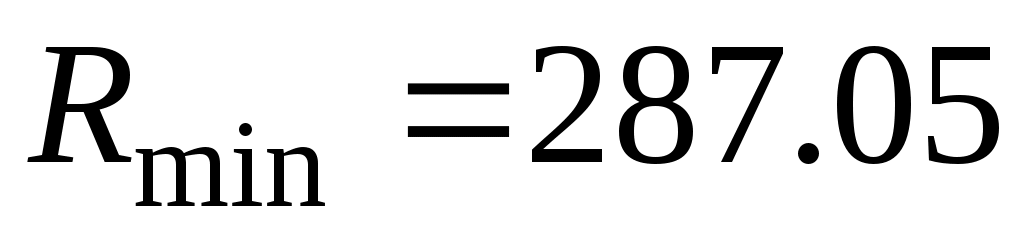 Ом;
Ом;
Среднее квадратическое значение отклонений резисторов от номинального значения -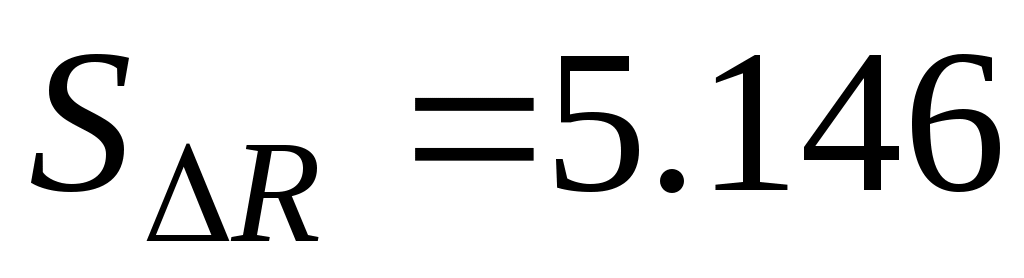 Ом.
Ом.
Примечание: для экономии места вся совокупность полученных результатов измерений резисторов здесь не приводится.В таблице 1 приведены сгруппированные по интервалам данные предварительной обработки отклонений резисторов от номинала.
Решение:
Для обоснованной формулировки гипотезы о виде закона распределения отклонений резисторов от номинала построим гистограмму опытного распределения, соблюдая все рекомендации, приведенные в 4-6, для чего:
Оценим величину остаточного члена по сравнению с другими погрешностями. Очевидно, что
Следовательно, линеаризация исходного уравнения правомерна и остаточным членом разложения можно пренебречь, при этом получаем
Принимая во внимание тот факт, что значения аргументов по условию задачи измерялись путем обыкновенных однократных прямых измерений, следует считать, что пределы относительных погрешностей аргументов
Следовательно, для определения пределов относительной погрешности измерения мощности следует воспользоваться формулой (2.35 [4] ), записав ее для относительных погрешностей:
Приняв доверительную вероятность
Учитывая, что суммируются всего две составляющие погрешности, оценим их арифметическую сумму
Так как
Ответ:
Задача № 2.17
Оценить границы неисключенного остатка методической погрешности измерения напряжения по условиям задачи № 2.15.
Решение:
Абсолютное значение методической погрешности определяется формулой (см. задачу № 2.15)
Вычислить точное значение поправки
Учитывая, что функция
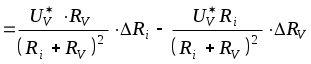 .
.Погрешности аргументов известны в виде границ, т. к. о законе распределения ничего не известно, определяем границы погрешности результата по формуле (2.35) с учетом (3.14). Принимая во внимание тот факт, что приходится суммировать всего две составляющих, оценим максимально возможные границы погрешности определения поправки
Таким образом, границы неисключенного остатка методической погрешности в абсолютной форме
Границы неисключенного остатка методической погрешности в относительной форме
%.
Ответ:
Задача № 2.18
Обработать результаты многократных прямых измерений тока, проведенных одним и тем же прибором за достаточно малый промежуток времени. При измерении получены следующие результаты (в мА):
10,07; 10,10; 10,15; 10,16; 10,17;
10,20; 10,40; 10,13; 10,12; 10,08.
Считать, что полученная совокупность результатов свободна от систематических погрешностей и подчиняется нормальному закону распределения.
Решение:
Из условия задачи следует, что полученная совокупность результатов представляет собой выборку равноточных нормально распределенных данных. Используя формулы раздела 2.3 [4], получаем:
1) Наиболее вероятное значение измеренной величины (оценка действительного значения тока)
2) Оценка средней квадратичной погрешности (СКП) экспериментальных данных
3) В полученной совокупности экспериментальных данных седьмой результат
Определим
Зададим доверительную вероятность
следовательно, результат
.
4) Уточняем значения
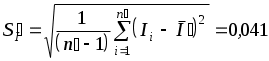 (мА).
(мА).В оставшейся совокупности результатов следует проверить еще результат
Так как
5) Определим СКП результата измерения (за результат измерения принимается уточненное значение
6) Определим границы доверительного интервала для результата измерений. Так как число обрабатываемых результатов
Границы доверительного интервала для результата измерения
7) Запишем результат измерения с указанием доверительной погрешности (соблюдая все правила метрологии при округлении значения погрешности и значения результата при окончательной записи результата измерений).
или 10,099 мА
Ответ:
или 10,099 мА
Примечание: обе записи результата соответствуют требованиям стандарта и являются равнозначными.
Задача № 2.19
Для выяснения закона распределения случайных отклонений изготовленных резисторов от номинала было проведено измерение точного значения 200 резисторов из одной партии. Номинальное значение резисторов 300 Ом. В результате предварительной обработки результатов измерений получены следующие данные:
Максимальное значение резистора в выборке -
Минимальное значение резистора в выборке -
Среднее квадратическое значение отклонений резисторов от номинального значения -
Примечание: для экономии места вся совокупность полученных результатов измерений резисторов здесь не приводится.В таблице 1 приведены сгруппированные по интервалам данные предварительной обработки отклонений резисторов от номинала.
Решение:
Для обоснованной формулировки гипотезы о виде закона распределения отклонений резисторов от номинала построим гистограмму опытного распределения, соблюдая все рекомендации, приведенные в 4-6, для чего: