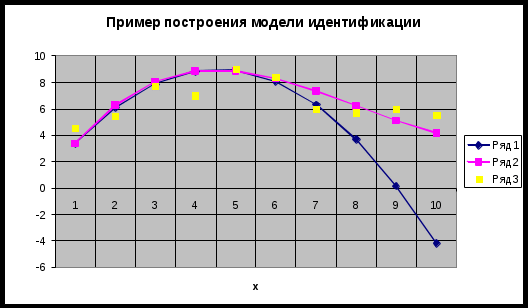
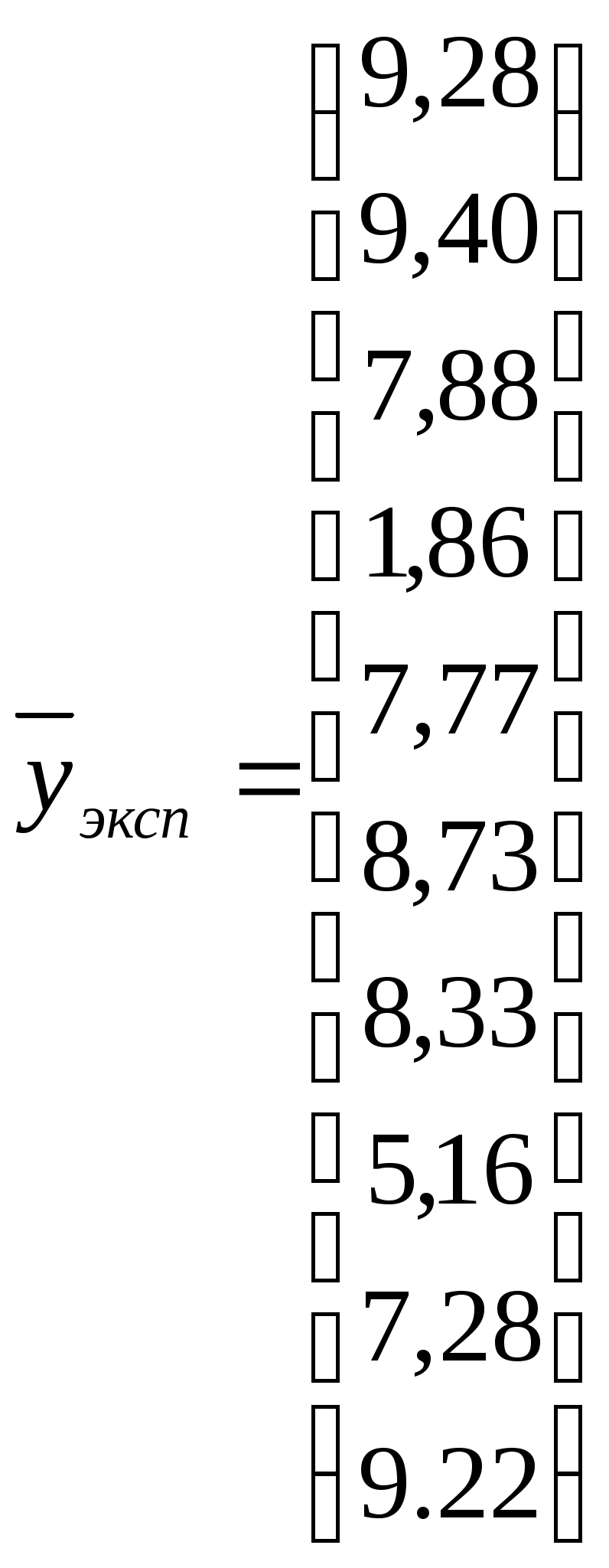
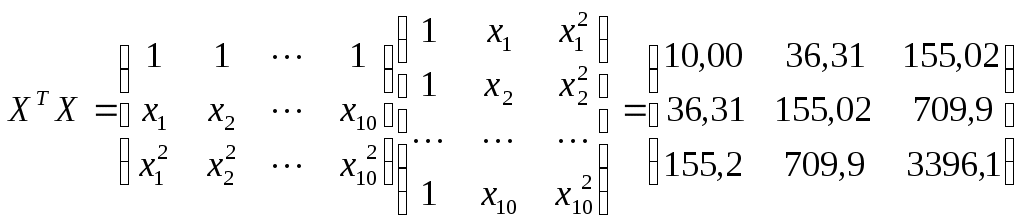
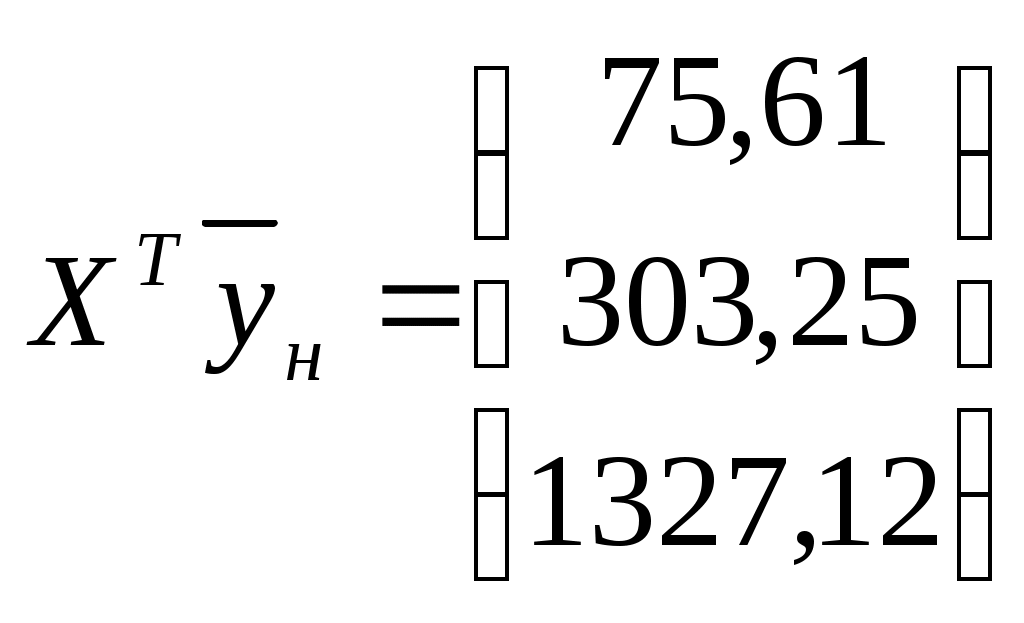
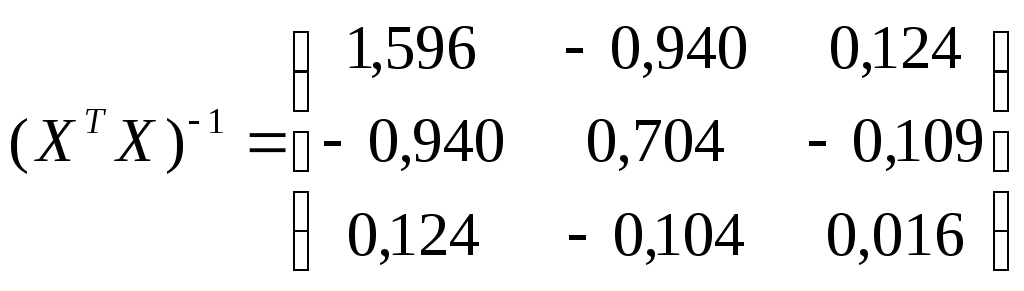
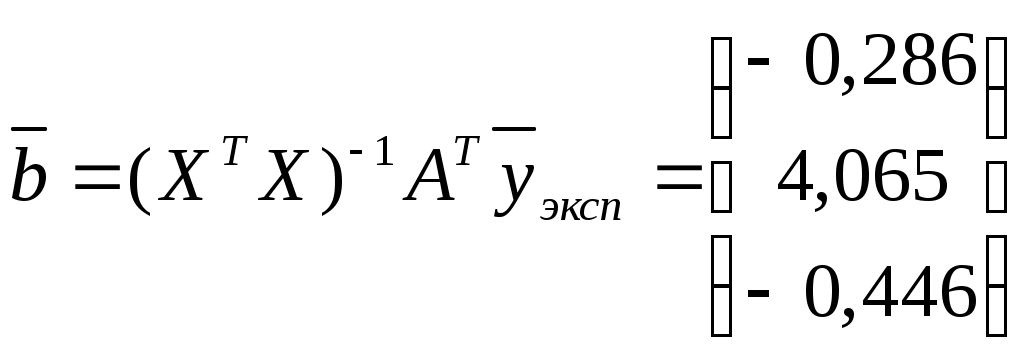
Результаты математического эксперимента (выборка 10 случайных пар ), представлены в виде точек на рис.1.1 (ряд 3).Построим модель идентификации . Согласно методу наименьших квадратов, искомый вектор коэффициентов находится из решения нормального уравнения . (1.4)Найдем составляющие уравнения (1.4)Таким образом, получена зависимостьна рис.1.1- ряд 2. Из рисунка видно, что полученная модель качественно правильно воспроизводит исходное описание.Статистические характеристики модели имеют следующие значения:

• 
  остаточная сумма квадратов
  

;

• 
  число степеней свободы остаточной суммы квадратов
  

• 
  средние квадраты остаточных сумм
  

;

• 
  критерий Фишера
  

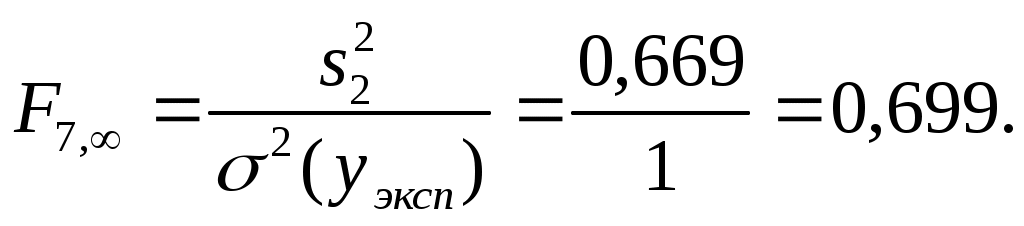
По таблицам распределения критерия Фишера , при 5%-м уровне значимости находим критическое значение . Так как полученное значение F меньше критического, гипотеза об адекватности модели реальному процессу принимается.Определим связи коэффициентов регрессии между собой

---

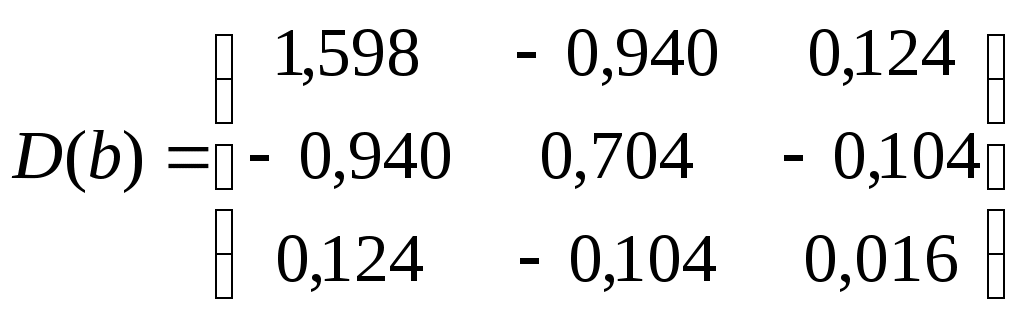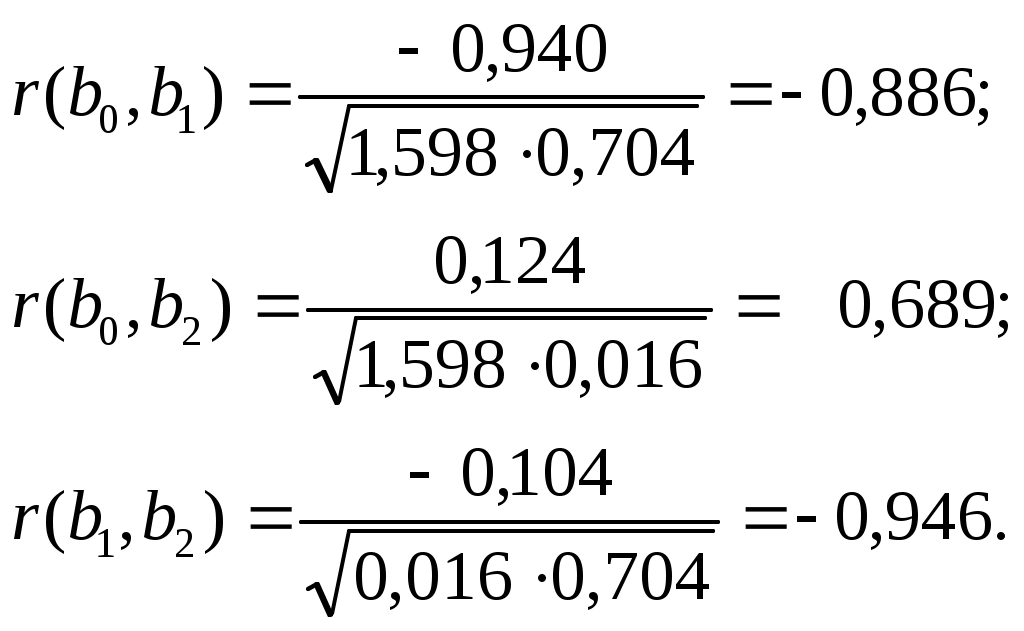
;Таким образом, коэффициенты регрессии достаточно сильно связаны между собой.Поскольку форма модели заранее неизвестна, целесообразно рассмотреть возможность использования кубической модели .В результате расчетов найдены коэффициенты такой модели (1.5)на рис.1.1 – ряд 1.Для проверки целесообразности включения в модель члена третьей степени вычисляется остаточная сумма квадратов для уравнения (1.5), дополнительная сумма квадратов, средний квадрат и величина Фишера: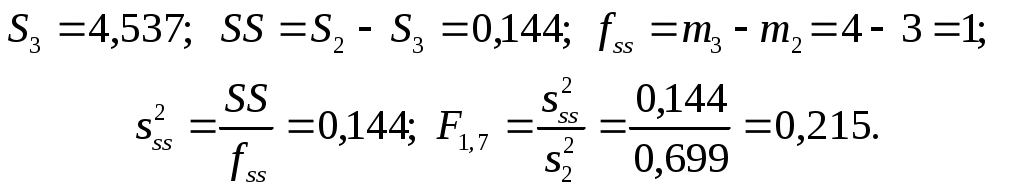По таблицам распределения (прил. 1) определяем критическое значение Фишера В связи с тем, что полученное из расчета значение критерия Фишера меньше критического, можно считать, что член третьего порядка не добавляет существенной информации и, следовательно, нецелесообразен. Лабораторная работа № 2

---

Тема: «Планирование экспериментов»Цель работы: Изучение основных понятий, определений, принципов теории планирования экспериментов, приобретение навыков проведения экспериментов по построению математических моделей, ознакомление с методикой построения регрессионных моделей.2.1.Задания

1. 
   Задан план эксперимента в виде матрицы. Каждая i – я строка матрицы образует точку плана, а j - й столбец - результаты функции отклика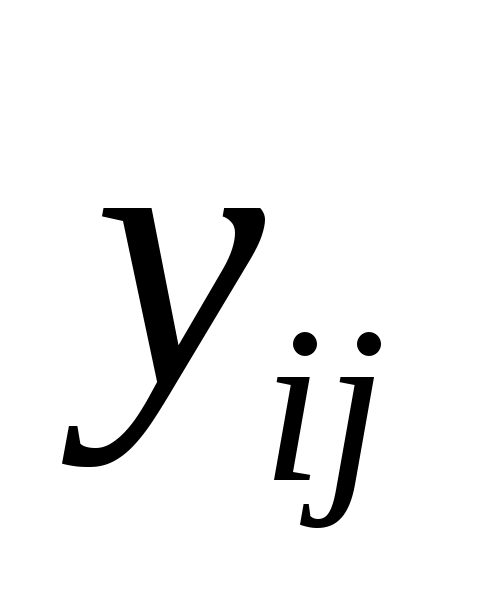 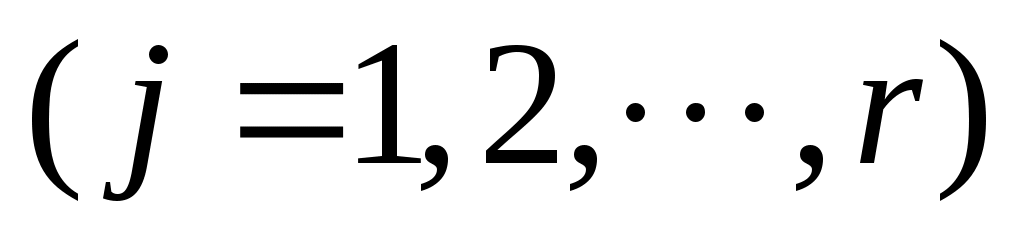в r параллельных экспериментах.
   
2. 
   В соответствии с вариантом задания построить план проведения полного факторного эксперимента типа .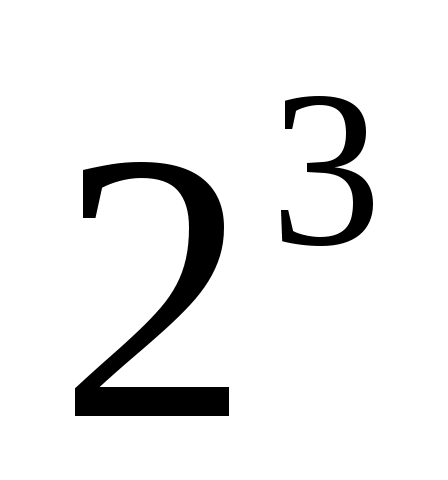
   
3. 
   Выполнить нормировку факторов, используя следующие значения нулевых уровней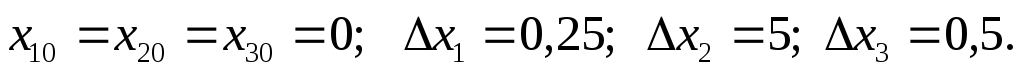
   
4. 
   Определить коэффициенты уравнения регрессии.
   
5. 
   Проверить значимость коэффициентов уравнения регрессии по критерию Стьюдента.
   
6. 
   Проверить адекватность модели оригиналу с помощью критерия Фишера.
   

2.2. Исходные данные для выполнения лабораторной работыВариант 1

3,004	3,031	3,035	3,039	3,001
5,193	5,152	5,177	5,209	5,151
3,927	3,950	3,936	3,898	3,897
7,141	7,099	7,111	7,138	7,097
4,684	4,697	4,688	4,730	4,729
9,135	9,123	9,166	9,134	9,117
6,371	6,403	6,343	6,339	6,337
14,672	14,680	14,695	14,668	14,672

---

Вариант 2

3,651	3,605	3,653	3,592	3,627
6,547	6,514	6,535	6,562	6,581
4,761	4,793	4,816	4,792	4,801
9,515	9,566	9,534	9,552	9,528
5,828	5,847	5,842	5,905	5,886
13,041	13,081	13,051	13,089	13,063
8,364	8,371	8,338	8,365	8,366
25,575	25,563	25,611	25,578	25,534

Вариант 3

2,124	2,150	2,139	2,140	2,157
3,382	3,394	3,368	3,374	3,372
2,705	2,652	2,655	2,674	2,713
4,307	4,242	4,276	4,317	4,255
3,107	3,089	3,096	3,119	3,137
5,081	5,148	5,123	5,092	5,073
3,948	3,901	3,914	3,951	3,919
6,873	6,920	6,932	6,858	6,869

Вариант 4

2,588	2,597	2,542	2,537	2,539
4,191	4,165	4,152	4,129	4,138
3,201	3,231	3,202	3,199	3,248
5,509	5,453	5,448	5,511	5,445
3,793	3,830	3,850	3,789	3,852
6,718	6,752	6,760	6,709	6,743
4,963	4,966	5,001	4,952	5,007
9,738	9,753	9,702	9,746	9,737
7,094	7,126	7,149	7,102	7,158

---

Вариант 5

3,072	3,028	3,080	3,049	3,069
5,193	5,159	5,163	5,220	5,168
3,932	3,955	3,893	3,915	3,939
7,094	7,126	7,149	7,102	7,158
4,740	4,704	4,668	4,698	4,724
9,163	9,167	9,160	9,133	9,191
6,336	6,396	6,369	6,405	6,357
14,676	14,668	14,725	14,722	14,741

Вариант 6

4,292	4,285	4,333	4,304	4,277
8,385	8,390	8,404	8,421	8,390
5,881	5,886	5,847	5,900	5,909
13,349	13,332	13,357	13,342	13,356
7,389	7,368	7,439	7,419	7,442
20,252	20,271	20,271	20,258	20,310
11,282	11,269	11,293	11,249	11,254
66,571	66,613	66,562	66,585	66,620

Вариант 7

4,307	4,284	4,284	4,316	4,286
8,387	8,396	8,430	8,389	8,404
5,832	5,873	5,856	5,843	5,862
13,329	13,304	13,328	13,340	13,312
7,379	7,415	7,415	7,368	7,368
20,255	20,278	20,304	20,279	20,261
11,226	11,238	11,271	11,234	11,273
66,599	66,605	66,588	66,595	66,562

---

Смотрите также файлы

• Реферат Таырыбы Титриметриялы анализ. Орындаан Кшербаева А.. химия31 студенті Мамандыы.docx

• Сталинградская битва. Начало коренного перелома. 17 Июля1941 2 февраля 1942 Период коренного перелома (Коренной перелом) радикальное изменение сил в ходе Великой Отечественной войны,.docx

• Федеральное агентство по техническому регулированию и метрологии.pdf

• Динамические системы и методы их математического моделирования в пакете Matlab Simulink.doc

• Аымды баылау 3 Таырып. Топыра ортасы жадайыны биоиндикациясы.docx