нүктесін 3 делік

3), шеңберлерінің қиылысу нүктелері

1 және 2 болсын

4) В' = f (В) нүктесі

5) ' = f () шеңбері (бұл шеңбер1, 2, 3'

нүктелері арқылы өтеді, мұнда 3' = f (3))

6) ' шеңберіне В' нүктесі арқылы өтетін

' жанамасын жүргізіп, оның А нүктесі

арқылы өтпейтінін аламыз

7)  = f (') – ізделінді шеңбер

Дәлелдеу: ' түзуі А нүктесі арқылы өтпейтіндіктен, оның образы А нүктесі арқылы өтетін шеңбер болады. Сонымен қатар ' түзуі В' нүктесі арқылы өтеді және ' шеңберімен жанасады, сондықтан В   және  мен  шеңберлері жанасады.

Зерттеу: Егер А, В нүктелерінің біреуі  шеңберіне қатысты ішкі, ал екіншісі сыртқы нүкте болса, есептің шешуі болмайды. А, В нүктелері  шеңберінің жанамасына тиісті нүктелер болса, онда есептің бір ғана шешімі бар. Қалған жағдайларда есептің екі шешімі болады.



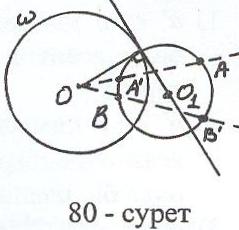
Есеп 2: Берілген А, В нүктелері арқылы берілген  (О, r) шеңберіне ортогональ шеңбер салыңыз.

Шешуі:

Талдау: Есеп шешілді делік,  ізделінді шеңбер

болсын. Егер  базистік шеңбер деп алсақ, ин–

версияда  шеңбері өз-өзіне көшеді (Теорема6)

және А, В нүктелерінің образдары сәйкесінше

осы шеңбердің А, В нүктелері болады (Теоре-

ма 4).  шеңберін анықтау үшін оның үш нүк –

тесін білсе болғаны (80-сурет): А, А, В.

Салу: 1)  шеңберіне қатысты инверсияда А нүктесінің образы: А нүктесі

2) А, А, В нүктелері арқылы  шеңбері

 - ізделінді шеңбер

Зерттеу: Егер А, В болса, онда А–ң образы өзі болады да, салу жоспарының бірінші қадамында В нүктесінің образы табылады.

Егер А, В болса, онда А, В нүктелерінен  шеңберіне жанама жүргізіп, олардың қиылысу нүктесін Р деп белгілейміз. Р – ізделінді шеңбердің центрі.

Егер А, В, О бір түзудің нүктелері және А, В өзара инверсиялы емес нүктелер болса, онда есептің шешімі болмайды.

Егер А, В, О бір түзудің нүктелері және А, В  шеңберіне қатысты инверсиялы нүктелер болса, онда есептің шексіз көп шешімі болады: А, В нүктелері арқылы өтетін кез – келген шеңбер  - ға ортогональ болады.

Есеп 3: а, в түзулері және олардан тысқары жатқан О нүктесі берілген. О нүктесінен берілген түзулерге дейінгі кесінділерінің көбейтіндісі берілген кесіндінің квадратына тең болатындай етіп сәуле жүргізіңіз.

Шешуі:

Т

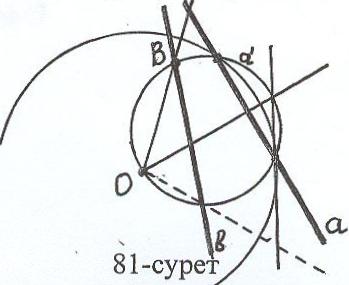
алдау:

---

Есеп шешілді, ОD ізделінді сәуле делік (81-сурет). r берілген кесінді, OD  a = A, OD  в = В болса, есеп шарты бойынша ОА  ОВ = r². Онда  шеңберіне қатысты инверсияда А нүктесі В–ға (инверсия анықтамасы бойынша), а түзуі а шеңберіне (Теорема3) көшеді және а шеңбері В нүктесі арқылы өтеді. Сонда В = а  в.

Салу: 1)  (О, r) шеңбері

2)  шеңберіне қатысты инверсияда

а түзуі а шеңберіне көшеді

3) В = а  в нүктесі

4) ОВ сәулесі

ОВ – ізделінді сәуле.

Дәлелдеу: Айталық А = ОВ  а, онда А -  шеңберіне қатысты В нүктесінің прообразы. Демек, инверсияның анықтамасы бойынша ОАОВ = r².

З

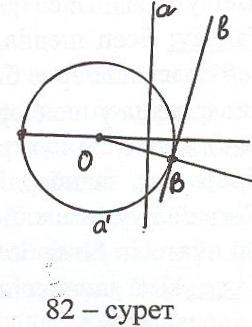
ерттеу: Келесі жағдайлар болу мүмкін:

1. 
   а  в қимасы екі нүктеден құралған,
   

онда есептің екі шешімі бар (82 – сурет);

2. 
   а  в қимасы бір нүктеден тұрады,
   

яғни а шеңбері мен в түзуі жанасады,

онда бір шешім болады;

3. 
   а  в = , онда есептің шешімі
   

болмайды.

Пайдаланылған әдебиеттер
1. Аргунов Б.И., Балк М.Б.,

Геометрические построения на плоскости, М. 1957

2. Атанасьян Л.С., Базылев В.Т.,

Геометрия (І часть), М. 1986

3. Атанасьян Л.С. и др.,

Геометрия 7– 9, Алматы 1996

4. Говоров В.М.,

Сборник конкурсных задач по математике, М. «Наука» 1986 г.

5. Готман Э.Г.,

Задачи по планиметрии и методы их решения, М.1996

6. Гусев В.А.,

Практикум решени математических задач

7. Қаниев С.,

Математикадан таңдамалы есептер (І кітап), Алматы 1993

8. Лурье М.В.,

Геометрия, Ростов-на-Дону 2002

9. Погорелов А.В.,

Геометрия 7 – 11, Алматы 1997

10. Саранцев Г.И.,

Сборник задач на геометрические преобразования, М. 1957

11. Солтан Г.Н., Солтан А.Е.,

Решение задач письменного экзамена по математике, Минск 2003

12. Шарыгин И.Ф.,Бүкүбаева К.О., Геометрия 7 – 9, Алматы 2004

13. ИФМ журналы,

1993ж №3 және №4, 1997ж №5, 1999ж №2, 2000ж №2, 2001ж №3

---

14. Математика және физика журналы,

2002ж №2, 2003ж №2 және №3

15. Математика – 1 сентября газеті,

2001ж №31, №32, №34 және №36, 2004ж №47

16. Математика в школе 1990ж №6

---

Смотрите также файлы

• Природные пожары.docx

• Практическая работа к теме Семья традиции Тема занятия Тема Моя семья традиции и ценности Класс 2.docx

• Тжірибелік сабаа арналан тапсырмалар Фт заттар мен энергия алмасу Тапсырма1. Анытама берііз Заттар мен энергия алмасу дегеніміз.docx

• Общий объем аудиторной работы обучающихся с овз в случае увеличения срока обучения на один год не может составлять менее 6018 академических часов за шесть учебных лет.docx

• Введение Открытие предприятия по производству детской игровой мебели из картона с целью выхода на новый сегмент рынка детской мебели и игрушек и получения прибыли.docx