- есеп шартын қанағаттандыратын өзара тең емес кейбір Ф₁, Ф₂, ..., Ф_n фигуралары салынса,

- есеп шартын қанағаттандыратын кез - келген фигура осы фигуралардың біріне тең болатыны дәлелденсе.

Бұл жағдайда есептің әр түрлі n шешуі бар делінеді.

2) Егер есептің шартында ізделінді фигураның берілген фигураға қатысты нақты орналасуы көрсетілсе, онда толық шешу берілген шартты қанағаттандыратын барлық фигураларды салу болып табылады (егер мұндай фигуралардың саны шекті болса). Сондай-ақ мұнда берілген фигураға қатысты әр түрлі қалыпта орналасқан тең фигуралар есептің әр түрлі шешулері болып саналады.

Кейде есеп шартын қанағаттандыратындай фигура болмауы мүмкін. Мысалы, берілген тіктөртбұрыш квадрат болмаса, оған іштей шеңбер сыза алмаймыз немесе концентрлі екі шеңберге ортақ жанама жүргізілмейді.

Кейде есептің шешімі бар, бірақ ол берілген құралдардың көмегімен салынбауы мүмкін. Онда салу есебін шешу деп ізделінді фигура берілген құралдардың көмегімен салынбайтындығын дәлелдеп көрсетуді айтады.

4. Қарапайым геометриялық салулар

Қарапайым есептердің шешулерін негізгі салуларға келтіру үшін де көптеген логикалық қадамдар жасауға тура келеді. Ал қиынырақ есептерді шешудің логикалық структурасын тұрғызу одан да қиынға соғады. Сондықтан күрделі есептерде қарапайым салу есептерін біле отырып, салу қадамдарын үнемдеуімізге болады, яғни қарапайым салуларды болашақта негізгі салуларға келтірмей - ақ қолдана аламыз.

Күрделі есептердің бөлігі ретінде жиі кездесетін қарапайым геометриялық салулар мектеп курсының бірінші Оларға мыналар жатады:

1. 
   Берілген кесіндіні қақ бөлу
   
2. 
   Берілген бұрышты қақ бөлу (бұрыш биссектрисасын салу)
   

3. 
   Берілген кесіндіге тең кесінді салу
   
4. 
   Берілген бұрышқа тең бұрыш салу
   
5. 
   Берілген түзуге одан тысқары нүкте арқылы параллель түзу жүргізу
   
6. 
   Берілген түзуге одан тысқары жатқан берілген нүкте арқылы перпен-дикуляр тұрғызу.
   
7. 
   Берілген кесіндіні берілген қатынаста бөлу
   
8. 
   Берілген үш қабырғасы бойынша үшбұрыш салу
   
9. 
   Берілген қабырғасы мен сол қабырғаға іргелес екі бұрышы бойынша үшбұрыш салу
   
10. 
    Берілген екі қабырғасы және олардың арасындағы бұрышы бойынша үшбұрыш салу
    
11. 
    Берілген шеңберге берілген нүкте арқылы жанама жүргізу
    
12. 
    Берілген гипотенузасы мен катеті бойынша тікбұрышты үшбұрыш салу
    

5. Салу есептерін шешу әдістемесі

---

Конструктивті есептерді шешудің схемасын таңдау әдістемелік сұрақ болып табылады. Геометриялық салу есептерін шешу төмендегі схема бойынша жүргізілгенде ғана дұрыс деп саналады:

1) Берілгендерді таңдауда барлық мүмкіндіктерді қамтитын жағдайлардың ақырлы саны белгіленеді;

2) Әрбір жағдай үшін есептің шешуі болу - болмауы және шешімі болса, олардың саны анықталады;

3) Әрбір жағдай үшін есептің шешімі болса, көрсетілген геометриялық құралдардың көмегімен оларды салу тәсілдері беріледі немесе оның берілген құралдармен салынбайтындығы көрсетіледі.

Күрделі есептерде оны шешудің мүмкін болатын жағдайларын, барлық шешімдерін, шығарылу тәсілін және т.б. анықтау үшін қалай талдау жасау керектігі жөнінде сұрақ туады. Сондықтан конструктивті есептер мына схема бойынша шешіледі:

1. 
   Талдау
   
2. 
   Салу
   
3. 
   Дәлелдеу
   
4. 
   Зерттеу
   

Әрине, бұл схема міндетті және өзгеріссіз емес, оның кейбір сатыларын қатаң түрде ажыратып, көрсетілген қалыпта ғана орындау мүмкін бола бермейді. Алайда конструктивті есептерді шешуде бұл схеманың көмегі мол. Енді схеманың әр этаптарына жеке тоқталып өтейік:

1.Талдау. Бұл - салу есебін шешудің ең негізгі және «әзірлеуші» бөлімі, себебі есепті шешудің кілті осында. Талдаудың мақсаты – есептің ізделінді элементтері мен берілгендері арасындағы байланысты тағайындау арқылы оның шешу тәсілдерін іздестіру. Оған берілген мен ізделінді фигураларды есеп шартында көрсетілгендей қалыпта орналастыратын көмекші сызба арқылы қол жеткіземіз. Бұл сызбаны «қолдан» сызуға болады. Әдетте, талдау жасау «есеп шешілді делік» деген сөздермен басталады. Көмекші сызбаны, негізінен, берілгендерден емес, ізделінді фигуралардан бастап салған дұрыс. Мысалы, бір төбесінен жүргізілген медиана, биссектриса және биіктігі бойынша үшбұрыш салу керек болса, алдымен кез - келген үшбұрыш сызып, содан соң оның есеп шартында көрсетілген сызықтарын жүргізген ыңғайлы. Егер көмекші сызбадан ізделінді фигураны салудың тәсілдері анық көрінбесе, онда ізделіндінің бөлігін немесе оны тұрғызу кезінде қолданылатын қандай да бір фигураны табамыз.

2

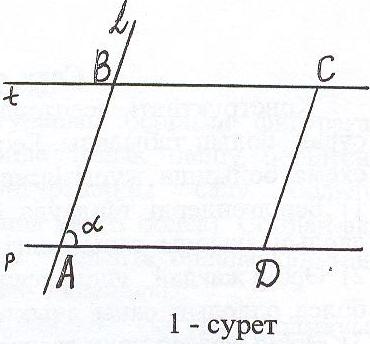
.Салу. Бұл бөлімде нәтижесінде ізделінді фигура шығатындай негізгі салу-лар (немесе бұрын шешілген, шығарылған есептер) тізімі беріледі. Салудың әрбір қадамы көрсетілген құралдың көмегімен графикалық көркемделіп отырылады. Мысалы, көршілес екі қабырғасы және олардың арасындағы бұрышы бойынша параллелограмм салу есебінің салу жоспары төмендегіше болады (1-сурет):

---

1) кез - келген р түзуі

2) АDр кесіндісі

3) DАL бұрышы (-берілген)

4) АВАL кесіндісі (берілген қабырға)

5) В нүктесі арқылы t // р түзуі

6) ВСАD, ВСt кесіндісі

7) С, D нүктелерін қосамыз

АВСD-ізделінді параллелограмм.

3.Дәлелдеу. Дәлелдеудің мақсаты – салынған фигура шынымен де есеп шартын қанағаттандыратынын көрсету. Салудың әр қадамының орындала-тындығын дәлелдеу, әдетте, сөйлем түрінде беріледі. Дәлелдеуде мынаны ескеру керек: талдаудан шығатын салдар дәлелдеудің шарты болып табылады және, керісінше, талдаудың шарты дәлелдеудің салдары болады.

4.Зерттеу. Салу есептің қандайда бір жалғыз шешімін тұрғызумен шектеледі және ондағы барлық қадамдар орындалады деп есептелінеді. Ал есептің толық шешуін табу үшін мына сұрақтарға жауап беру керек:

1) берілген фигуралардың кез-келген орналасуында салу жоспары орындала ма

2) егер таңдалған салу әдісін басқа жағдайлар үшін қолдануға болмаса, ізделінді фигура қалай тұрғызылады

3) берілген фигуралардың әртүрлі орналасуында есептің мүмкін болатын шешулерінің саны қанша

Осы сұрақтардың әрқайсысына жауап беру есепті зерттеу болып саналады. Демек зерттеудің мақсаты – есептің шешілу шартын анықтап, оның шешімдерінің санын табу.

Зерттеу, негізінен, «салу бойынша», «салу барысында» сөздерімен басталады. Бұлай қабылдаудың негізгі мақсаты – салудағы әр қадамға тоқталып, ондағы іс - әрекеттердің әрдайым орындалу - орындалмауын тексеру, егер орындалса, неше әдіспен екендігін анықтау.

Есепті осылайша талқылаудың нәтижесінде берілген тәсілмен ізделінді фигураны салу мүмкіндігі белгілі болады. Бұл жерде «егер салудың қандай да бір тәсілін өзгертсе, есептің жаңа шешулері пайда болмай ма» деген сұрақ туады. Кейде есептің әрбір шешуі оның бұрын анықталған шешуімен сәйкес келетінін дәлелдеуге болады. Онда зерттеуді ары қарай жүргізіп қажет емес. Ал егер сәйкес келмейтіндігі дәлелденсе, онда басқа әдіспен анықталатын

шешулер болуы мүмкін болғандықтан, талдауға қайта оралып, берілген немесе ізделінді фигуралардың орналасуының басқа жағдайлары қарастырылады. Ал есеп айтарлықтай жеңіл болғанда, кейбір сатылар, мысалы талдау немесе зерттеу қарастырылмайды.

6. Салу есептеріне мысалдар

Есеп1: Бір төбесінен жүргізілген биссектрисасы, медианасы және биіктігі бойынша үшбұрыш салыңыз.

Шешуі:

---

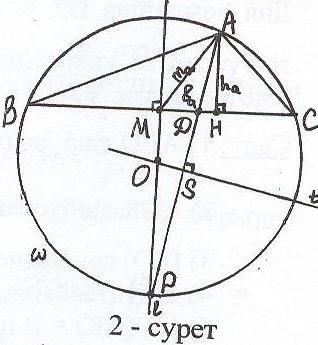
Талдау: Есеп шешілді делік, АВС – ізделінді үшбұрыш (2-сурет), АН – оның биіктігі, АМ – медианасы, АD – биссектрисасы.

АВС үшбұрышына сырттай шеңбер сызылған шеңбердің центрін О деп белгілейік, онда ОМ түзуі ВС хордасына перпендикуляр болғандықтан, ол осы хордамен керілетін шеңбердің әрбір екі доғасын тең екіге бөледі. АD биссектрисасы да  шеңберінің ВАС бұрышы тірелетін дәл осы доғасын тең екіге бөледі. Олай болса, ОМ түзуі мен АD биссектрисасы сырттай сызылған шеңбердің Р нүктесінде қиылысады. О нүктесінен АР – ға түсірілген перпендикулярдың табаны – АР-ның ортасы, яғни S нүктесі болады.

Салу: 1) АD = в_а гипотенузасы, АН = h_а катеті бойынша АНD үшбұрышы



2) (А, m_а) шеңбері

3) (А, m_а)  DН = М нүктесі

4) Мl және l  DН түзуі

5) l  АD = Р нүктесі

6) t - АР кесіндісінің орта

перпендикуляры

7) t  МР = О нүктесі

8) (О, ОА) шеңбері

9) DК   = В және С нүктелері

АВС – ізделінді үшбұрыш.

Дәлелдеу: Салу бойынша АН кесіндісі АВС үшбұрышының биіктігі болады. М – ВС қабырғасының ортасы, себебі ол шеңбердің центрінен ВС хордасына түсірілген перпендикулярдың табаны. Сондықтан АМ – медиана. Р нүктесі ВРС хордасының ортасы болғандықтан, іштей сызылған ВАР және САР бұрыштары өзара тең, бұдан АD – ВАС бұрышының биссектрисасы.

Зерттеу: Есептің шешімі болу үшін m_a  в_a  h_a қатынасы орындалуы қажет, себебі үшбұрышта биссектриса медиана мен биіктіктің ортасында орналасады, не бұл кесінділердің бәрі беттеседі. Егер m_a = в_a = h_a болса, онда есеп биіктігі (ол әрі медиана, әрі биссектриса) бойынша тең бүйірлі үшбұрыш салу есебіне келеді. Егер m_a  в_a  h_а болса, онда салу жоспарының 1) және 2) қадамдары бірмәнді орындалады. m_a  в_а болғандықтан, (А, m_а)  DН қимасының М нүктесі табылады. Салу жоспарының 5) қадамындағы Р нүктесі жалғыз, себебі ол екі түзудің қиылысу нүктесі. Сонымен қатар, АР||DН және МР  DН болғандықтан, АР||МР. Бұл АР хордасының орта перпендикуляры міндетті түрде МР түзуімен қиылысады дегенді білдіреді және ол нүкте сырттай сызылған шеңбердің центрі болады. DН түзуі (А, АР) шеңберімен екі нүктеде қиылысады, себебі ол шеңбердің ішіндегі D нүктесі арқылы өтеді. Сонда көрсетілген салу жоспары бойынша шешілген есептің шешімі әрдайым табылады.

---

Есеп 2: h_c, h_в биіктіктері және m_а медианасы бойынша үшбұрыш салыңыз.

Ш

ешуі:

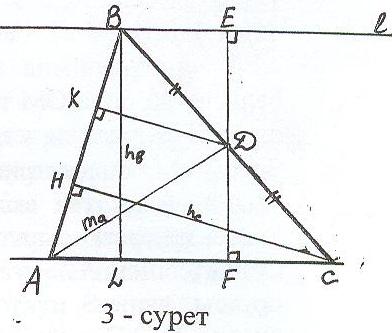
Талдау: Айталық, АВС – ізделінді үшбұрыш

(3 - сурет), АD = m_а, CH = h_c, BL = h_в.

АС табанына DF перпендикулярын жүргізсек,

DF = (D–медиананың табаны болғандықтан).

Олай болса, АFD тікбұрышты үшбұрышын

АD = m_а гипотенузасы мен DF = катеті

бойынша сала аламыз. Дәл осылайша DК = катеті мен АD гипотенузасы арқылы АDК тікбұрышты үшбұрышын тұрғызуға болады. Сонда ізделінді үшбұрыштың ВАС бұрышы анықталады.

Салу: 1) АFD тікбұрышты үшбұрышы (АD = m_а, DF = , DFА=90⁰)

2) АDК тікбұрышты үшбұрышы (АD = m_а, DК = , DFА=90⁰)

3) [FD) сәулесіне FЕ = h_в кесіндісі

4) Е нүктесі арқылы l║AF түзуі

5) l ∩ [AК) = В нүктесі

6) ВD түзуі

7) ВD ∩ [AF) = С нүктесі

АВС – ізделінді.

Дәлелдеу: Салу бойынша DF = , онда ЕF = h_в . Бұдан DЕ = DF = . Онда BED = DFC = 90⁰ екенін ескерсек, ∆DЕВ = ∆DFС. Олай болса, ВD = DС, яғни АD – медиана және салу бойынша АD = m_а.

В нүктесінен АС табанына ВL перпендикулярын түсірсек, BL = EF = h_в. Айталық СН  АВ, онда СНВ үшбұрышында DК кесіндісі (К АВ) орта сызық болады. Ал салу бойынша DК = . Бұдан СН = DК = h_с.

Зерттеу: Салу жоспарының 1) және 2) қадамдарындағы АDF, АDК үшбұрыш-тарын салу

m_а h_в, m_а h

---

Смотрите также файлы

• Природные пожары.docx

• Практическая работа к теме Семья традиции Тема занятия Тема Моя семья традиции и ценности Класс 2.docx

• Тжірибелік сабаа арналан тапсырмалар Фт заттар мен энергия алмасу Тапсырма1. Анытама берііз Заттар мен энергия алмасу дегеніміз.docx

• Общий объем аудиторной работы обучающихся с овз в случае увеличения срока обучения на один год не может составлять менее 6018 академических часов за шесть учебных лет.docx

• Введение Открытие предприятия по производству детской игровой мебели из картона с целью выхода на новый сегмент рынка детской мебели и игрушек и получения прибыли.docx