с гипотенузасы,  сүйір бұрышы

бойынша тікбұрышты үшбұрыш саламыз (60-сурет). Сонда  бұрышына ірге-лес жатқан катет ізделінді х кесіндісі, ал қарсы жатқан катет у кесіндісі болады.

2-мысал: х = a cos³, y = a sin³ формулаларымен берілген х, у кесінділерін салыңыз, мұнда а – берілген кесінді,  - берілген бұрыш.

Салу жоспары төмендегіше болады: (61-сурет)

1

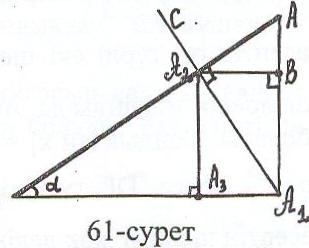
) АОА₁ =  бұрышы, ОА = а гипотенуза –

сы бойынша АОА₁ тікбұрышты үшбұрышы

2) А₁С  ОА түзуі

3) А₁С  ОА = А₂ нүктесі

4) А₂В  АА₁ (ВАА₁) түзуі

5) А₂А₃  ОА₁ (А₃ОА₁) түзуі

ОА₃, АВ – ізделінді кесінділер, яғни

ОА₃= a cos³, АВ = a sin³.

Ескерту1: х = a cosⁿ, y = a sinⁿ формулаларымен берілген кесінділерді жоғарда көрсетілген әдіс бойынша аналогиялық түрде салуға болады.

Ескерту2: х = a cos³, y = a sin³ (0    2) формулалары астроида деп аталатын қисық сызықты анықтайды. 2-ші мысалдағы салу жоспарын циркуль және сызғыштың көмегімен орындай отырып еш есептеусіз астроиданың кез-келген нүктелерін табуға болады.

3.4. Алгебралық әдіс арқылы шешілетін салу есептеріне мысалдар

Есеп 1: Үшбұрыш берілген. Оның ауданын тең екіге бөлетіндей етіп, табанына параллель түзу жүргізіңіз.

Шешуі:

Т

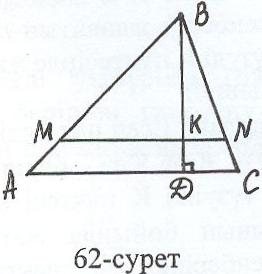
алдау: Айталық АВС–берілген үшбұрыш (62-сурет), АВ = с, ВС = a, AC = в және BD = h (BDC = 90⁰) делік. АВС үшбұрышының АС табанына MN параллель түзуін оның ауданын тең екіге бөлетіндей етіп жүргізу үшін К нүк-тесін, яғни ВК = х кесіндісінің ұзындығын

табу керек, мұндағы К = MN  BD.

АВС үшбұрышының ауданы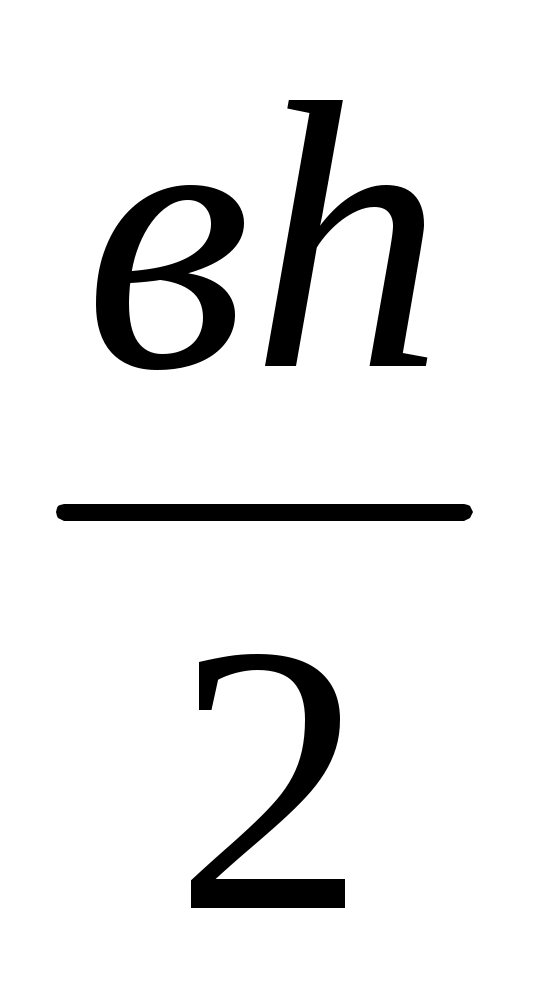 , ал BMN

үшбұрышының ауданы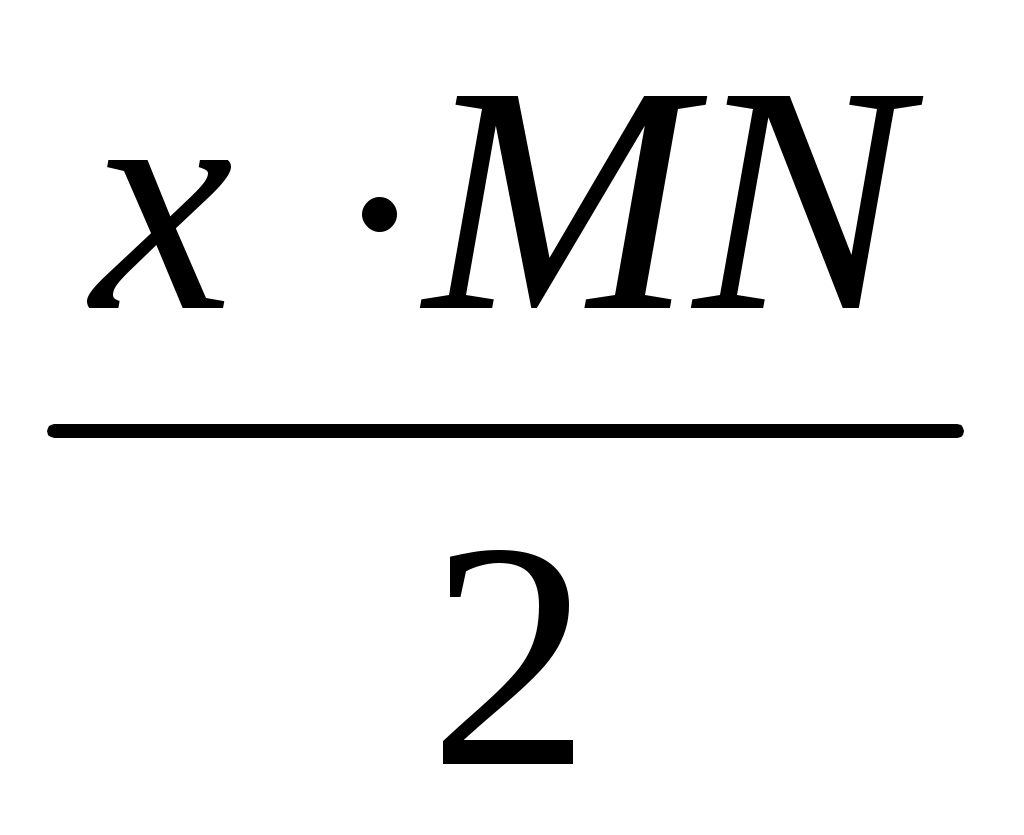 болады.

Есеп шарты бойынша

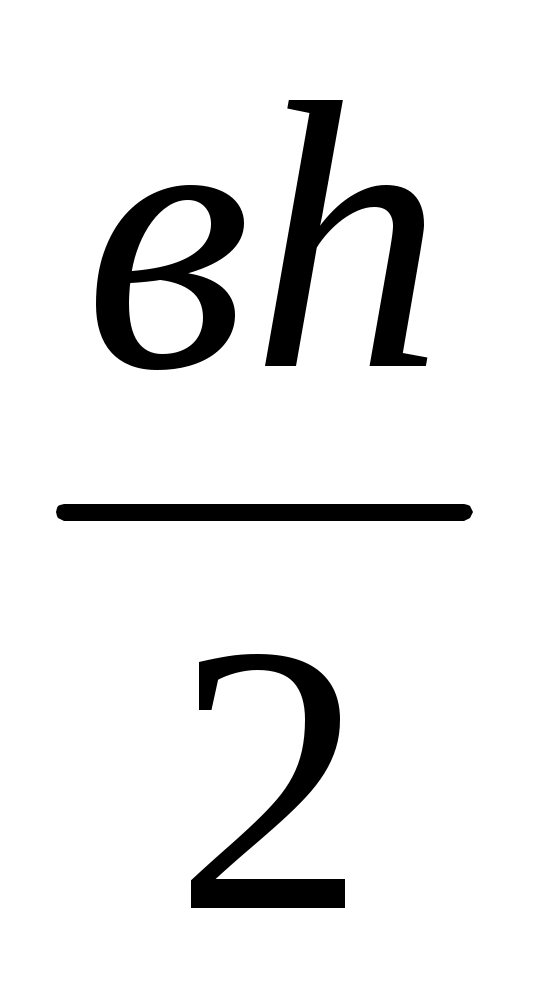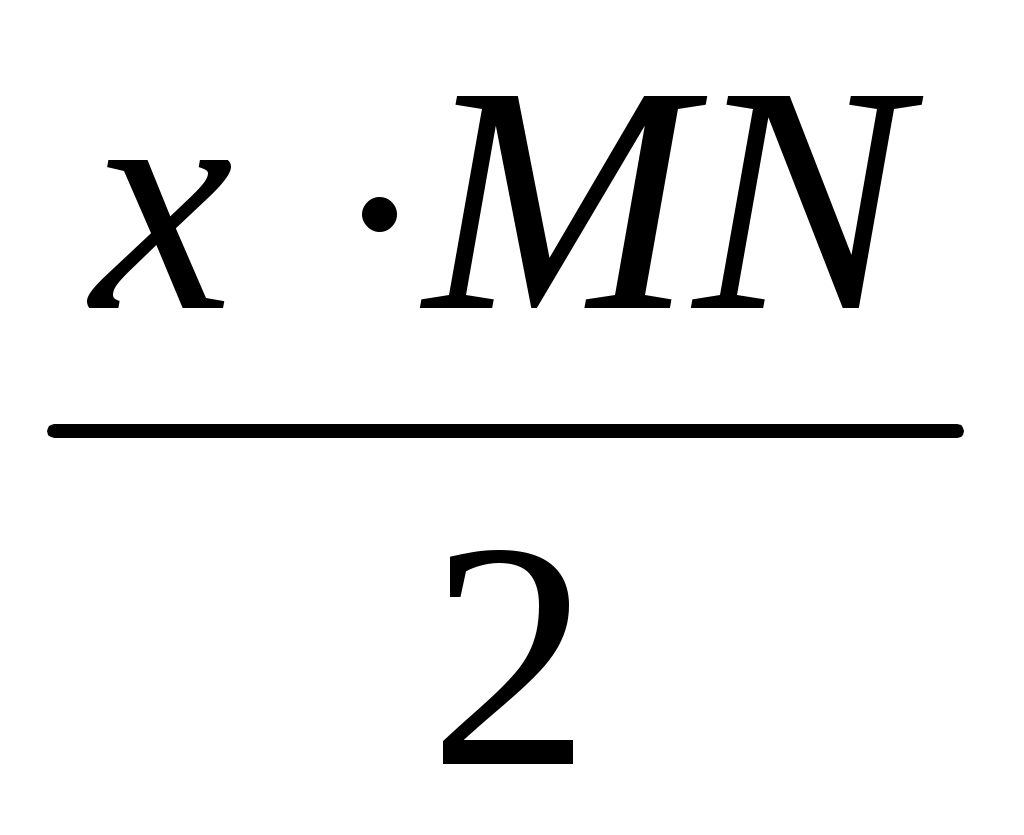= 2 (1)

Үшбұрыштың бір қабырғасына параллель жүргізілген түзу, сол үшбұрышқа ұқсас үшбұрыш қиятынын ескеріп, АВС  BMN деп жаза аламыз. Бұдан

---

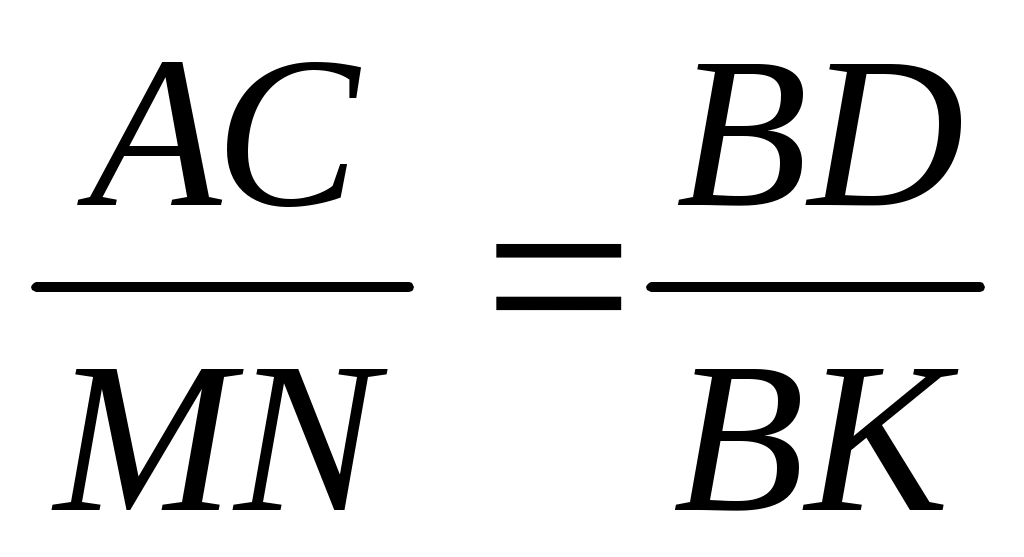немесе ,

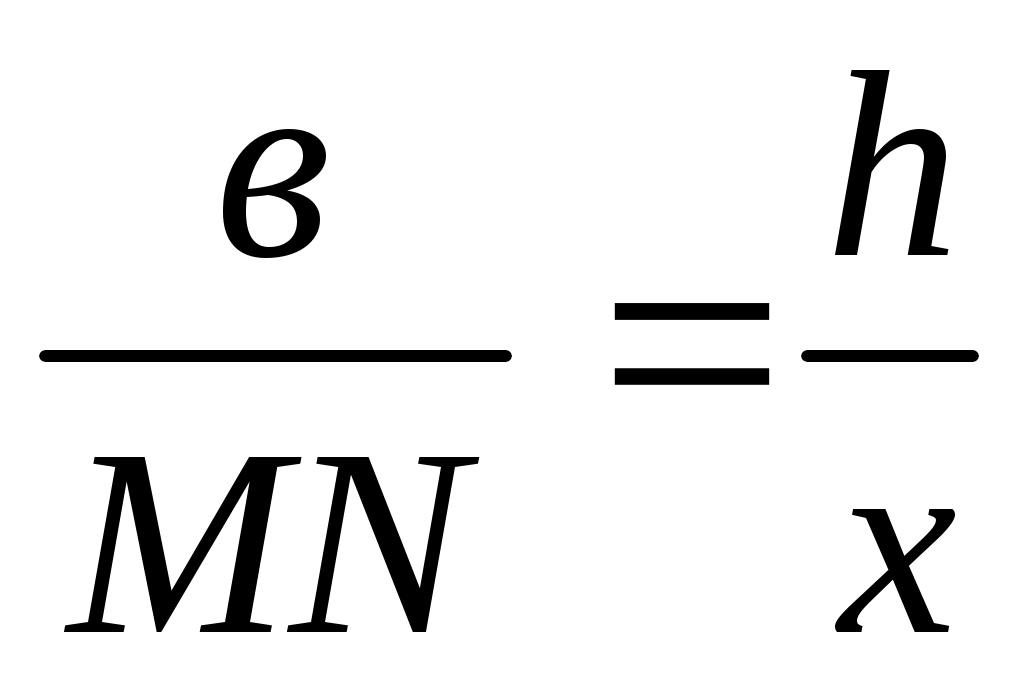онда MN =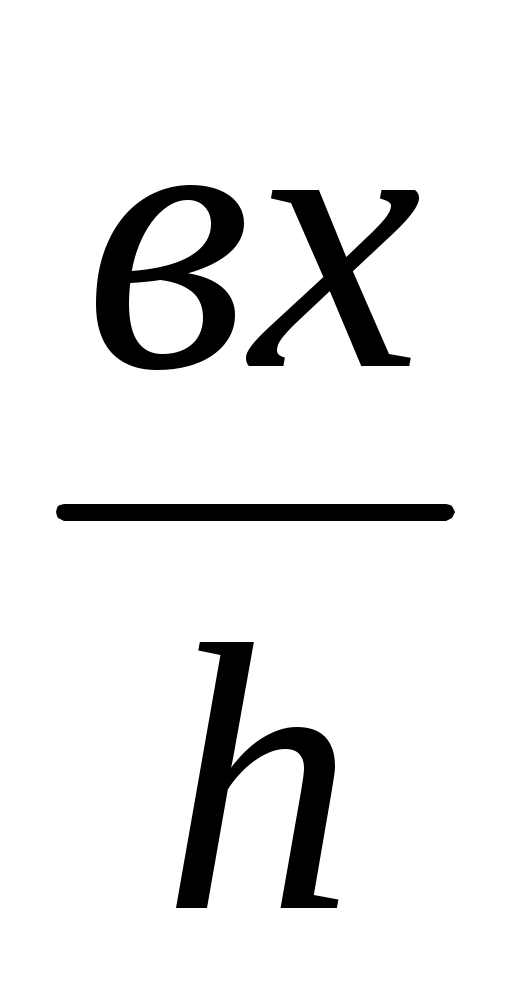 (2)

(1) және (2) теңдіктерін теңестіріп, ізделінді кесіндіні аламыз:

х =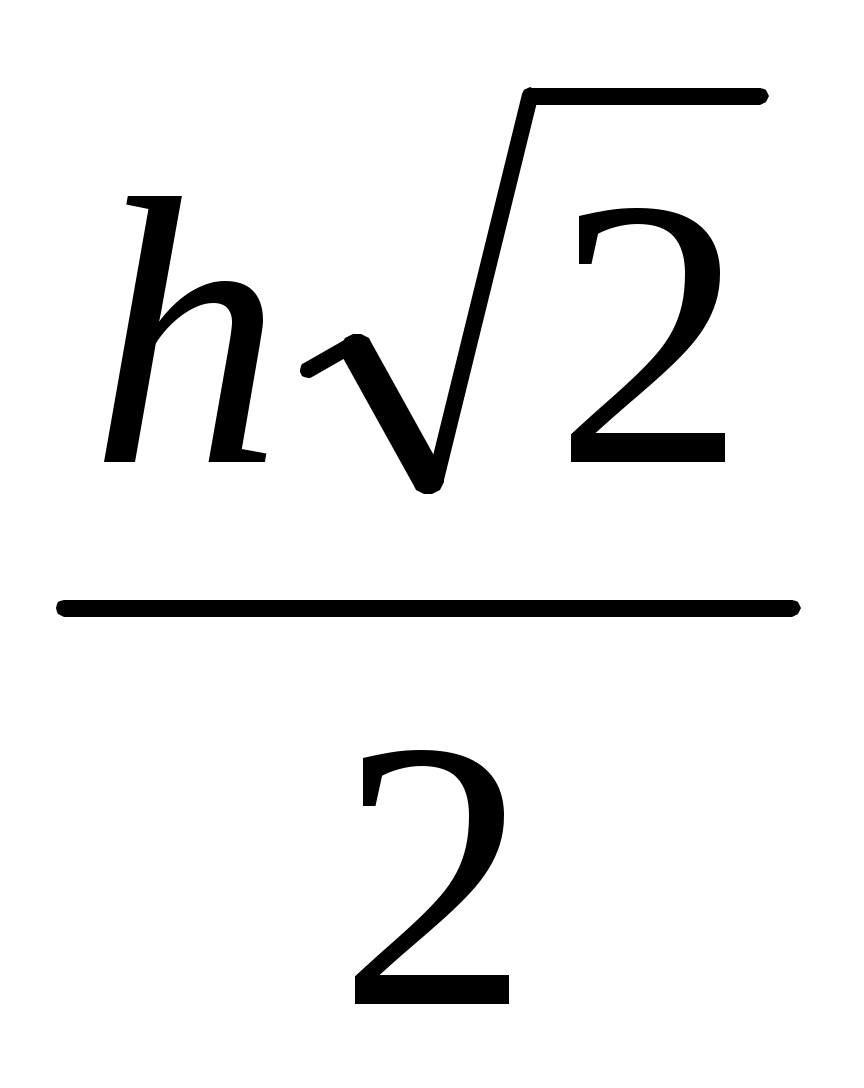 (3)

Салу: х =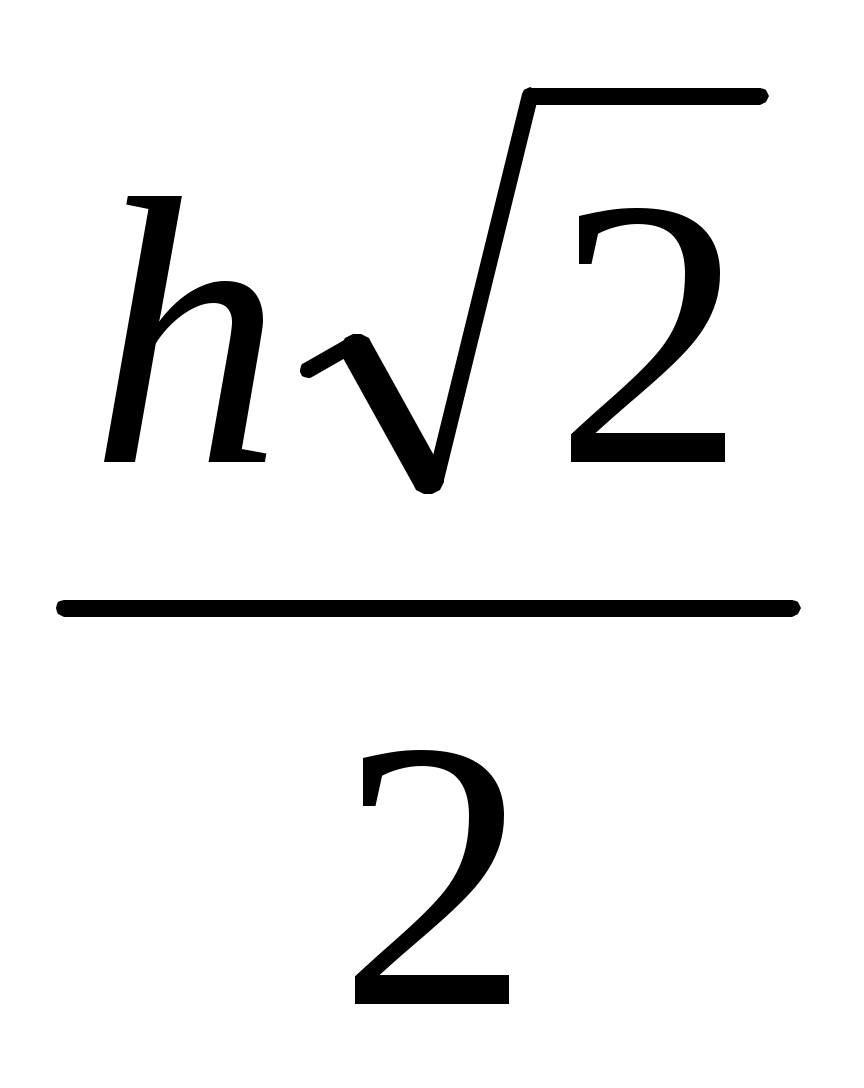 кесіндісін салу: қабырғасы BD = h (берілген АВС үшбұрышының биіктігі) болатын квадраттың диагоналы MB = h 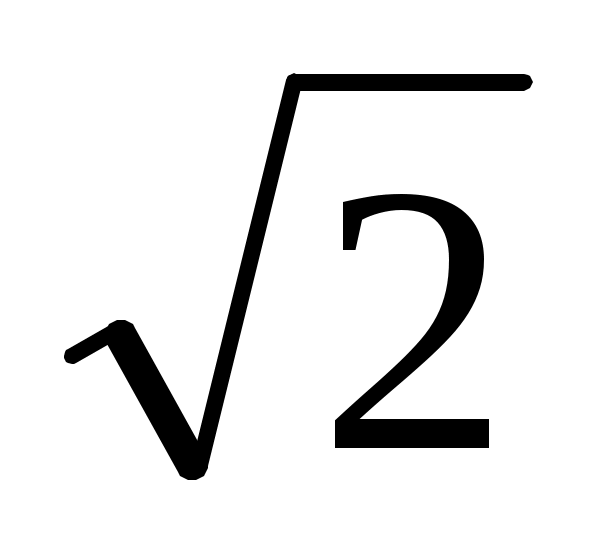(63 -

с

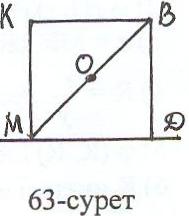
урет), онда оның жартысы ОВ = .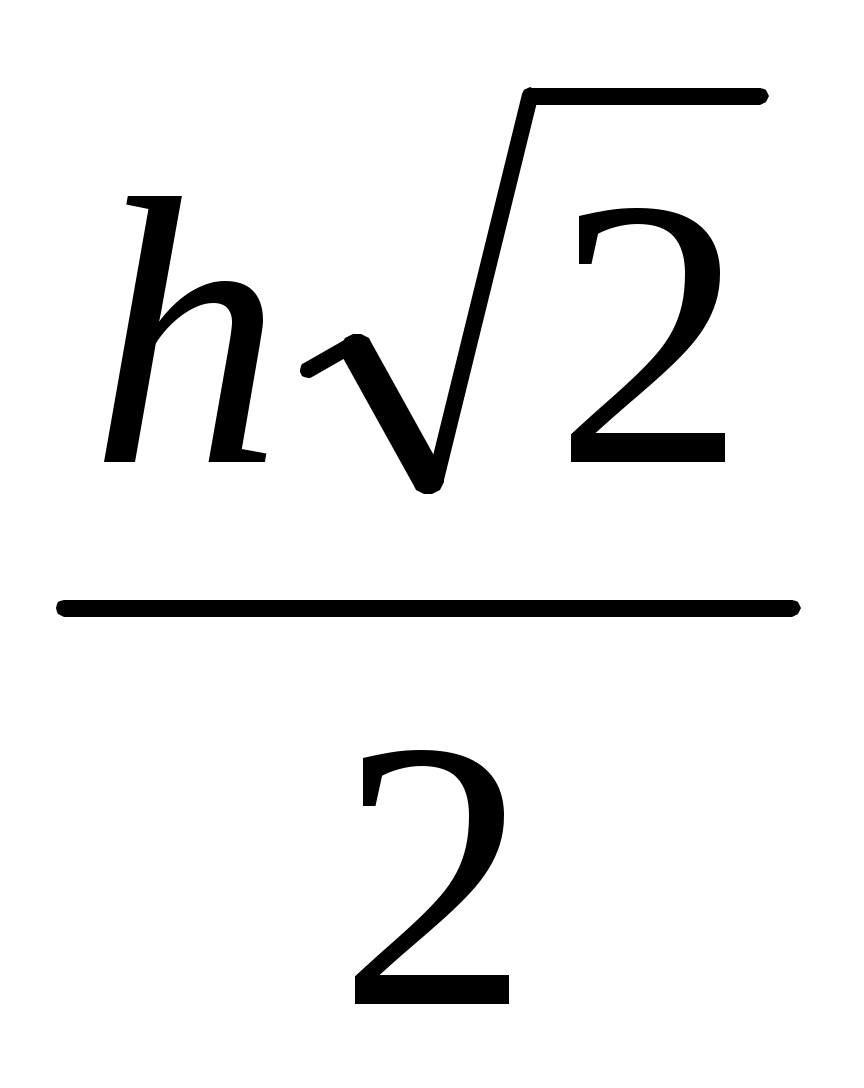

Осы табылған х = ОВ кесіндісін берілген

АВС үшбұрышының В төбесінен бастап,

h биіктігінің бойына өлшеп саламыз да,

АС қабырғасына параллель МК түзуін

жүргіземіз. МК – ізделінді түзу.

Дәлелдеу: Ізделінді К нүктесі арқылы жүргізілген МКАС түзуі берілген үшбұрыш ауданын тең екіге бөледі, онда

S_BMN = S_AMNC (4) теңдігін дәлелдейік. S_BMN = MNx = x = ;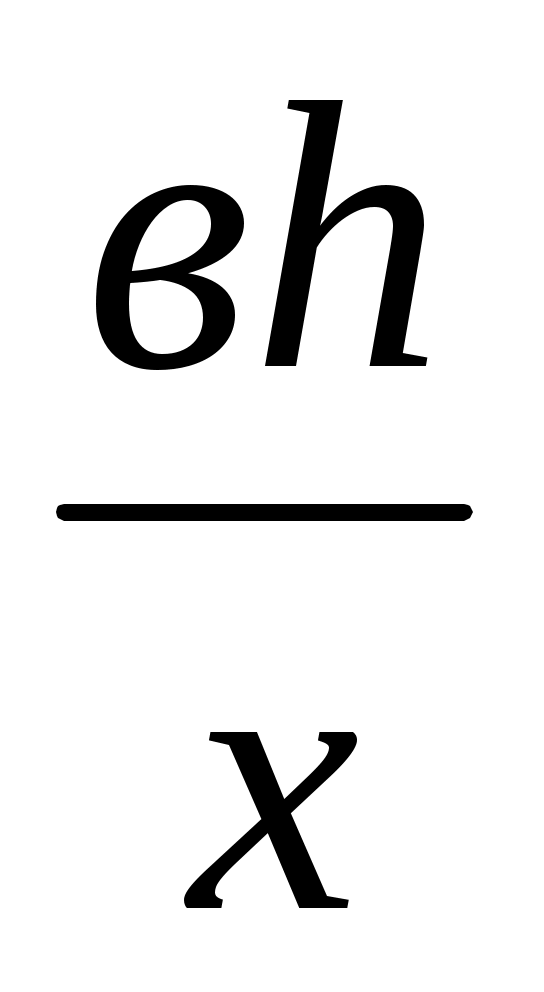

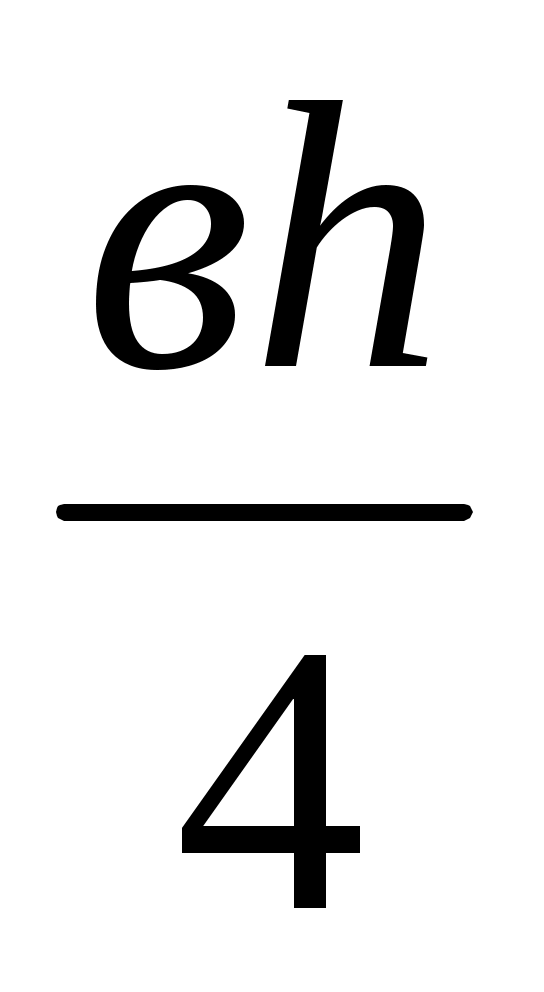S_AMNC = = = =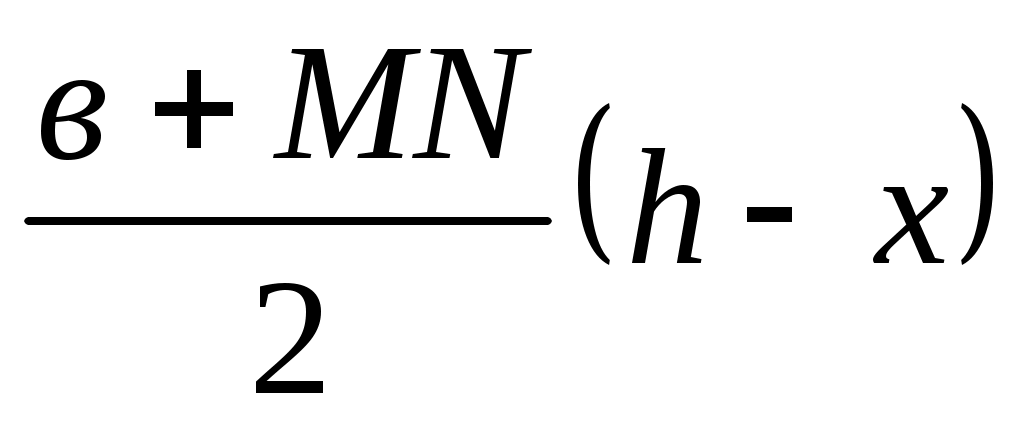

= = = .

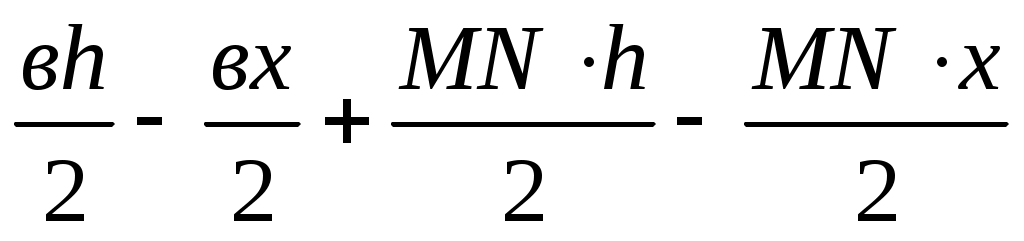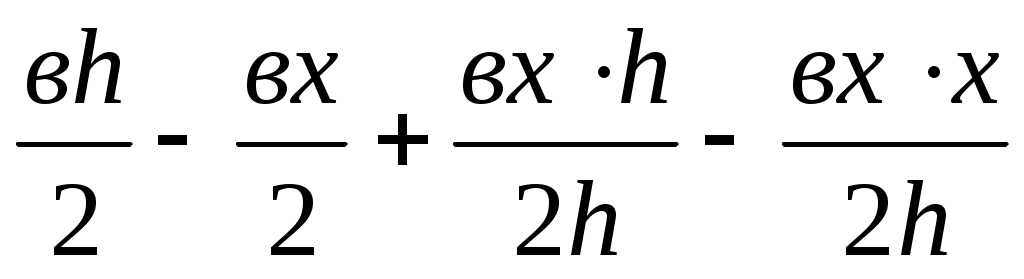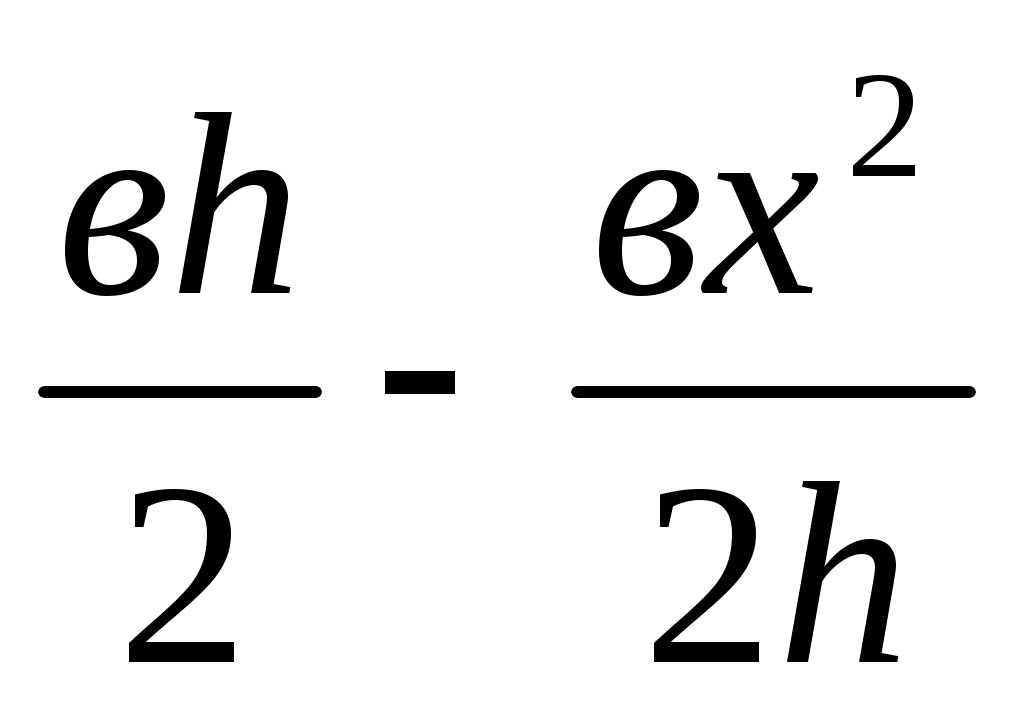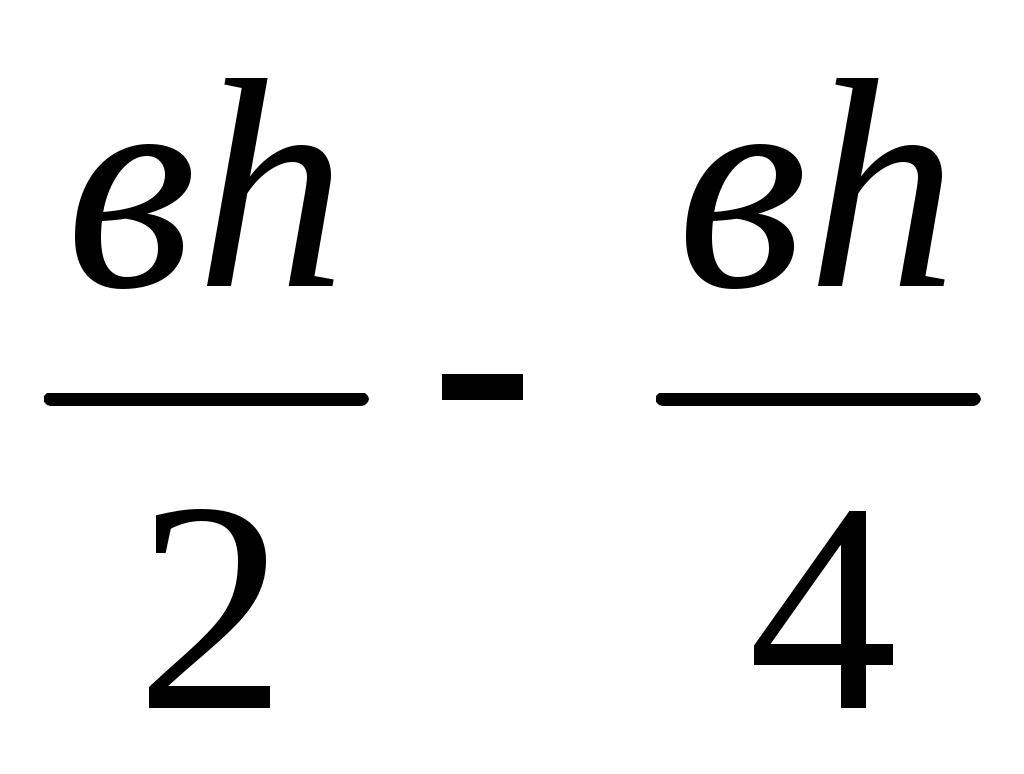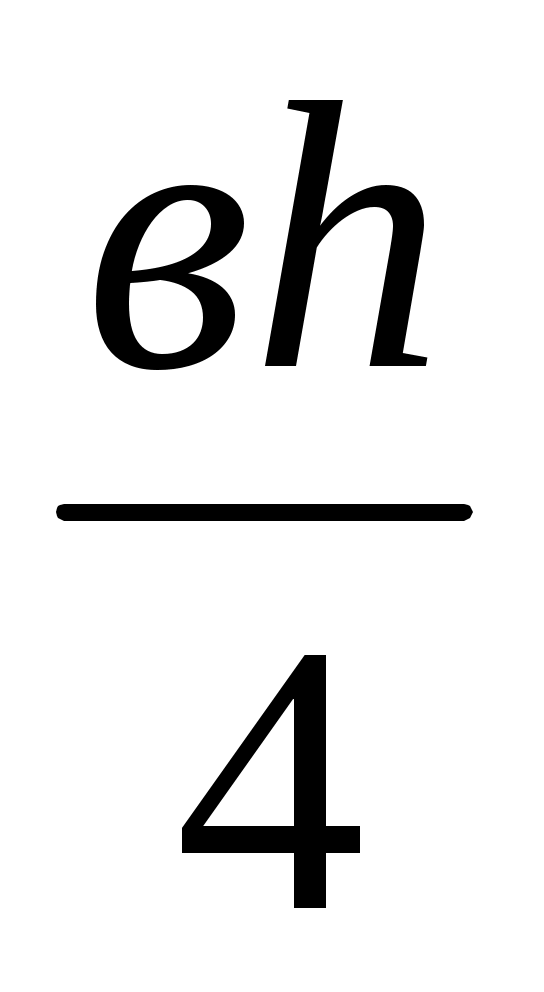Сонымен (4) теңдік орындалады, яғни К – ізделінді нүкте.

Зерттеу: х кесіндісінің шамасы (0, h) аралығында болады. Онда MN кесіндісінің ұзындығы АС-дан кіші. (3) өрнектегі h оң шама, сондықтан х те оң шама болады. Егер х 

---

h болса, есеп шарты орындалмайды. Сонда х(0, h) болғанда, есептің жалғыз шешімі бар.

Есеп 2:  шеңбері, К   нүктесі және К нүктесі арқылы өтіп,  шеңберін жанайтын m түзуі берілген. Берілген шеңбер мен берілген түзуді К нүктесінде жанайтын шеңбер салыңыз.

Шешуі:

Т

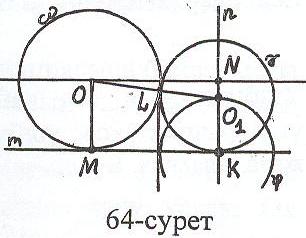
алдау: Есеп шешілді делік,  (О, r) – берілген шеңбер, m – берілген түзу, К, К  m – берілген нүкте (64-сурет). Ізделінді шеңбердің центрі m түзуіне К нүктесі арқылы жүргізілген n орта перпендикулярының бойында жатады және  (О, r) шеңберінен R қашықтықта болады, мұндағы R – ізделінді шеңбердің радиусы. m түзуіне О нүктесі арқылы параллель түзу жүргізіп, оның n түзуімен қимасын N деп белгілесек, ON = MK,

OM = NK = r. Ізделінді шеңбердің центрі О₁ болса,

О₁К = O₁L = R, ал O₁N = r – R.

мұндағы L – шеңберлердің жанасу нүктесі. Соны -

Сонымен ОО₁N үшбұрышынан Пифагор теоремасы

бойынша ON²+O₁N² = OO₁²  ON² + (r–R)² = (r–R)²

 ON² + r² – 2rR + R² = r² + 2rR + R² 

 ON² = 4rR  R = .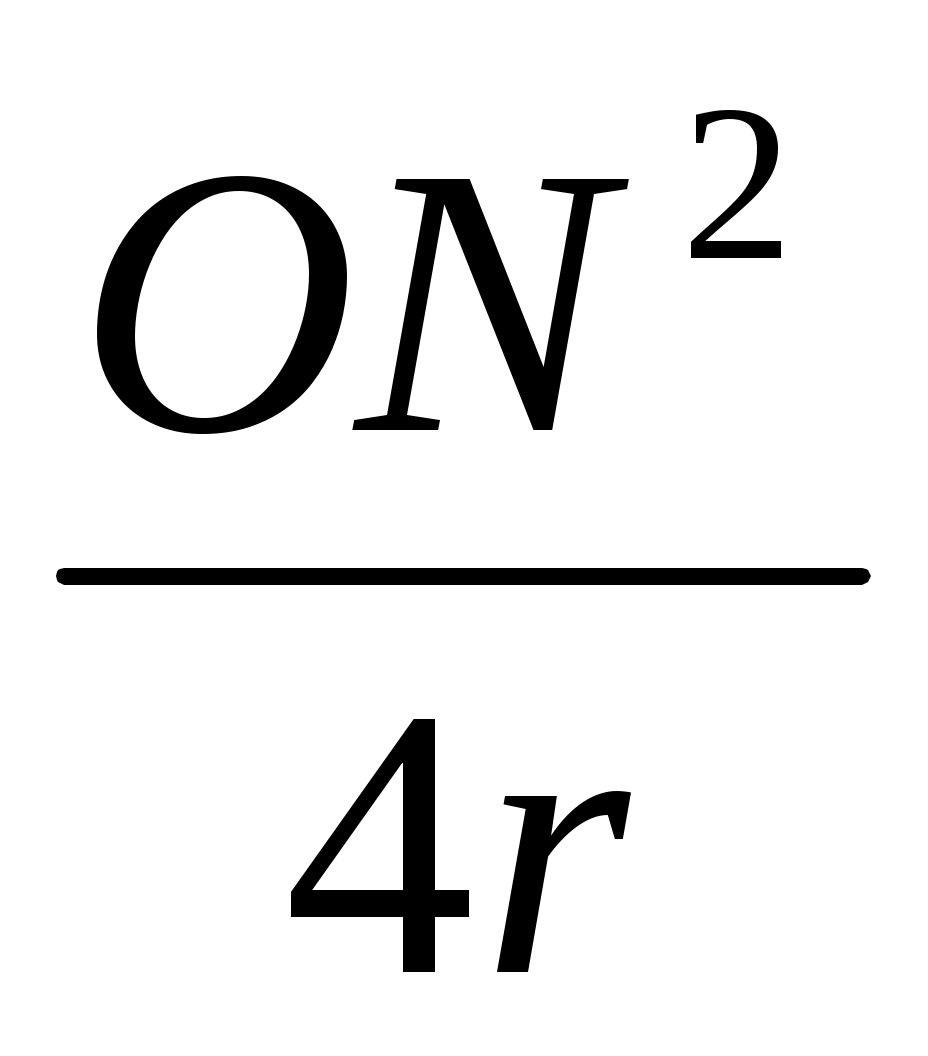

R – дің мәні күрделі өрнек болып шықты. Бұл өрнекті алгебралық әдіспен салуға болады.

Салу: 1) у = 4r кесіндісі

2)  (О, r)  m = М нүктесі

3) z = МК кесіндісі

4) R =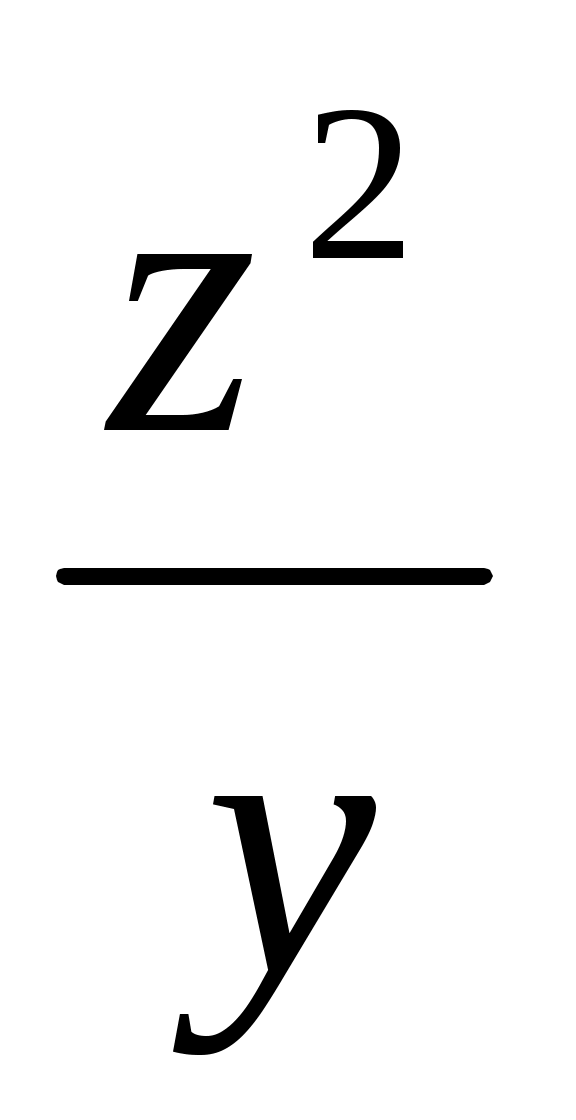 кесіндісі

5)  (К, R) шеңбері

6) К нүктесі арқылы n  m түзуі

7)   n = О₁ (О₁ – m түзуінің  шеңбері жатқан жағындағы нүкте)

8)  (О₁, R) шеңбері

 - ізделінді шеңбер.

Дәлелдеу: 5) және 7) салу бойынша О₁К = R. Ал О₁  n, онда  шеңбері мен m түзуі жанасады.

ОО₁ = = = =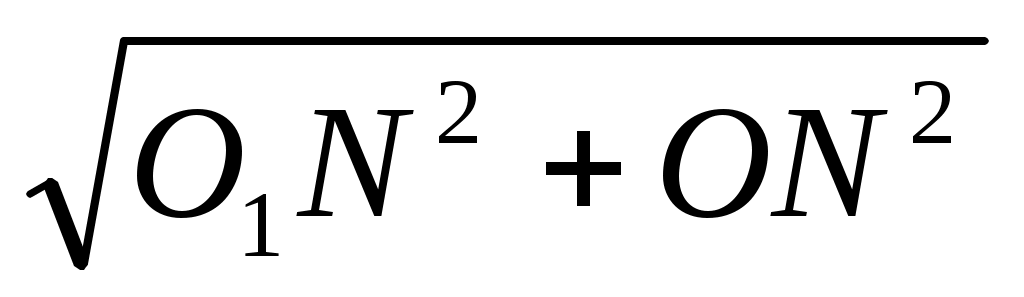

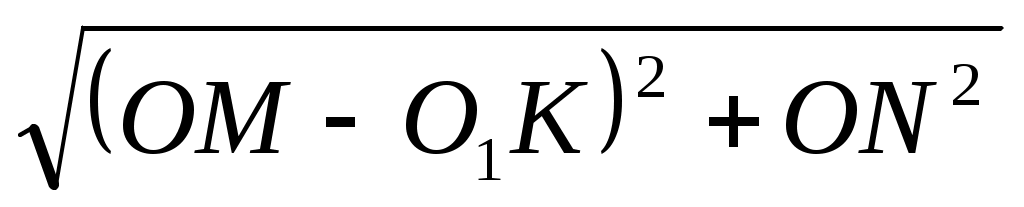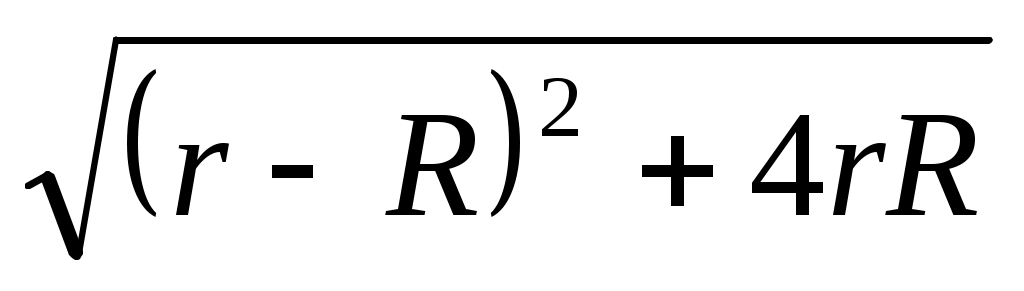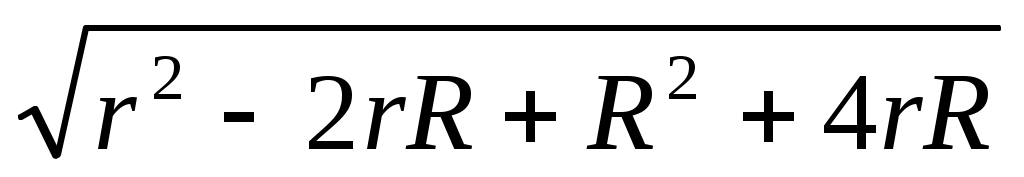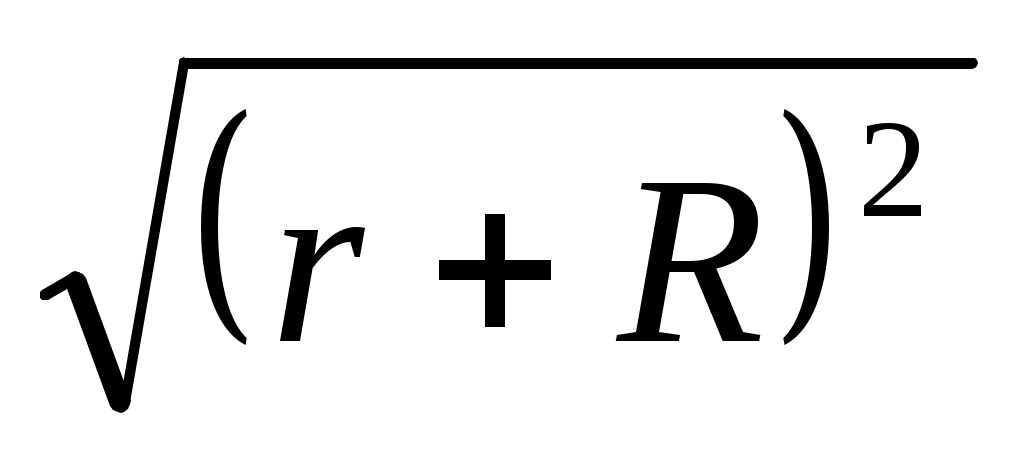= = = r + R,

онда ,  шеңберлері жанасады.

Зерттеу: R =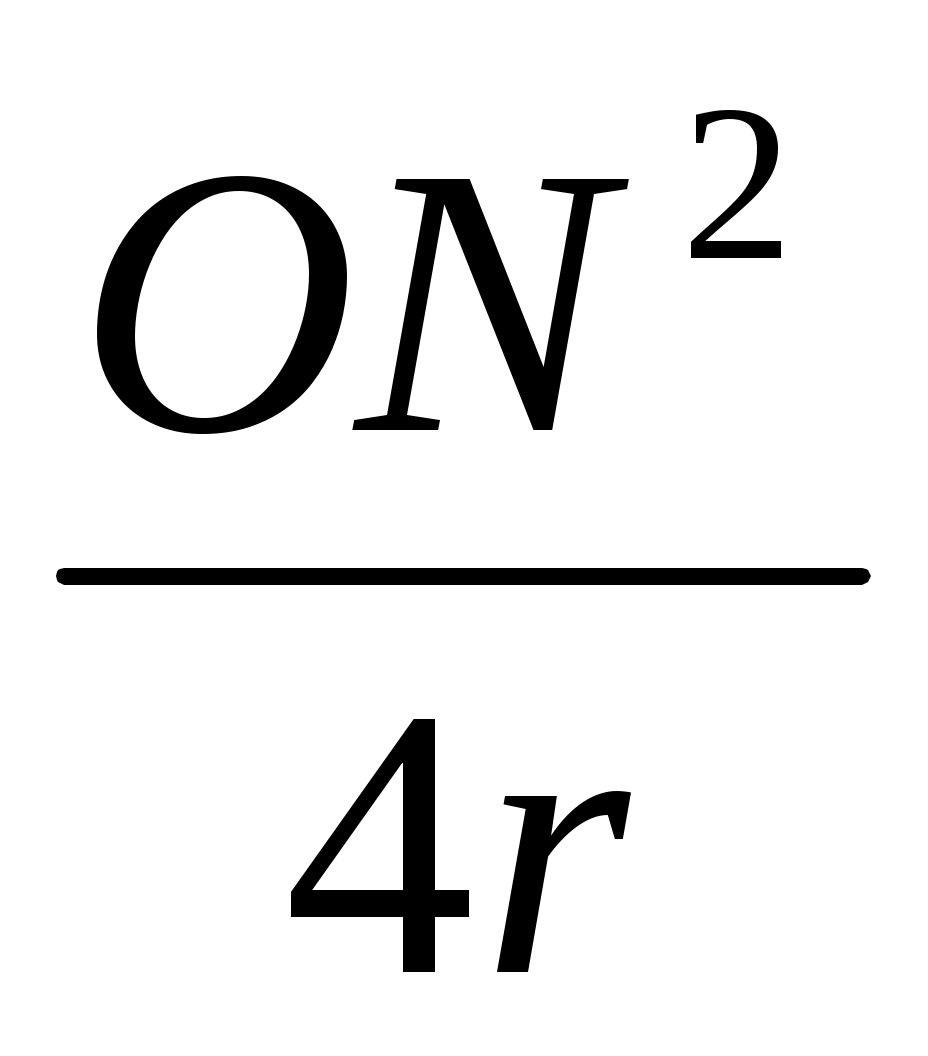

---

. ON, r кесінділердің ұзындығы болғандықтан, оң шамалар болады. Онда R кесіндісі де табылады және бірмәнді. Олай болса, есептің жалғыз шешімі болады.

Есеп 3: Гипотенузасы және тік бұрышының биссектрисасы бойынша тікбұрышты үшбұрыш салыңыз.

Шешуі:

Талдау: Есеп шешілді делік, АВС – ізделінді үшбұрыш (65 – сурет). CD - берілген биссектриса, АВ– берілген гипотенуза. CD   (О, ОВ) = Е деп белгі-лесек (О–сырттай сызылған шеңбердің центрі), ЕОАВ және CDDE = ADDB.

Б

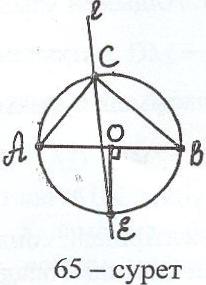
ұдан lDE = (AO – OD)(OB + OD)

l DE =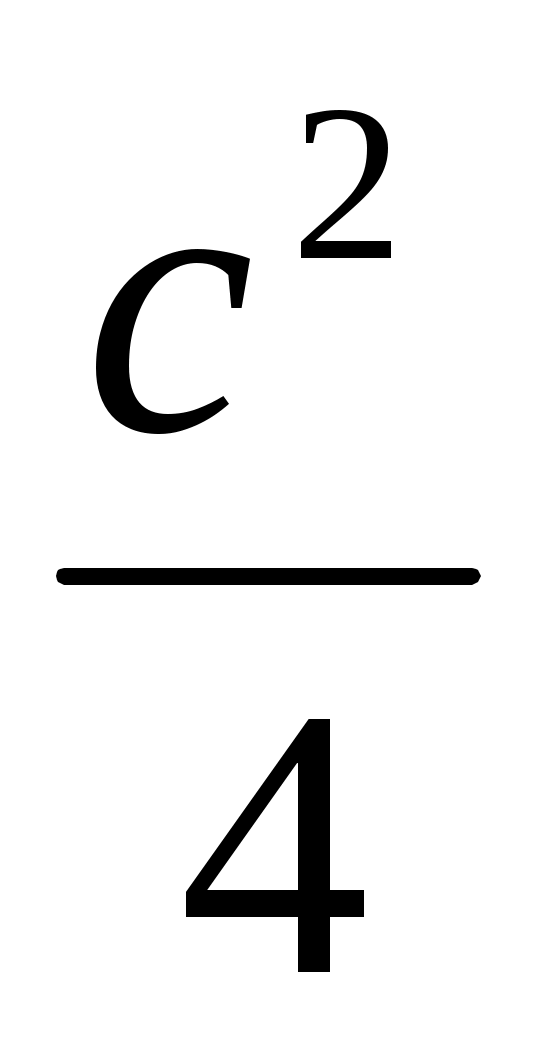 - (DE² - ) 

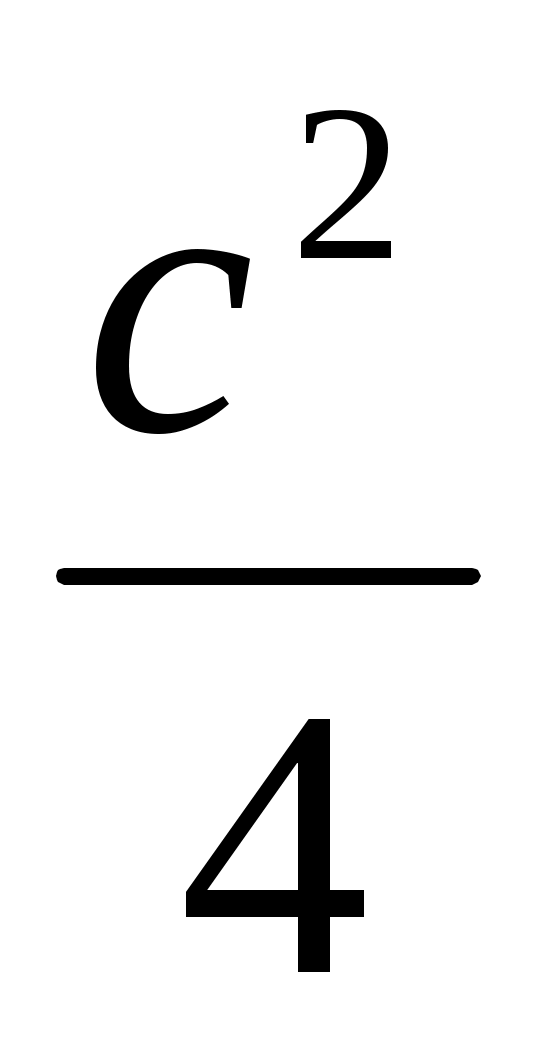 l DE =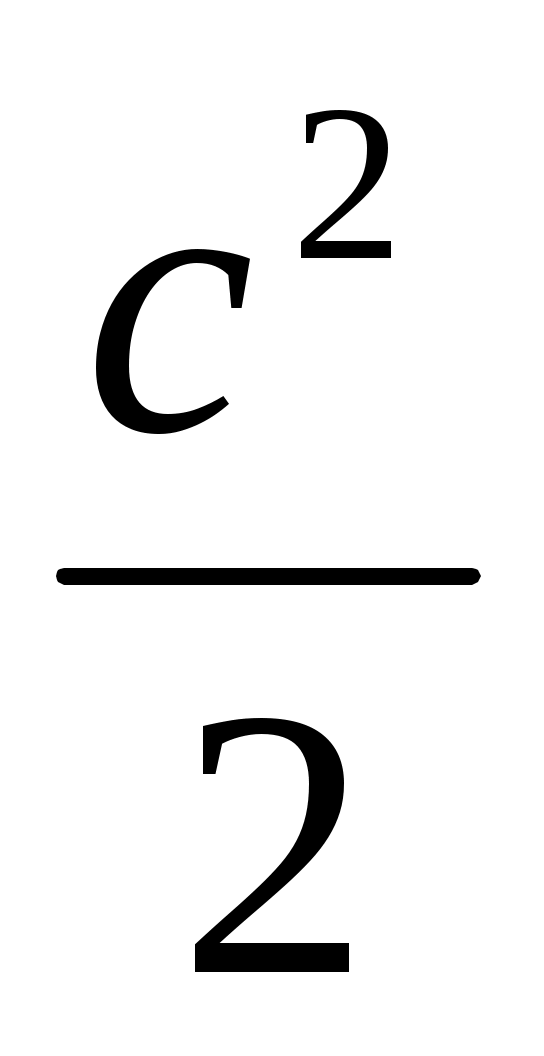 - DE² 

 DE = .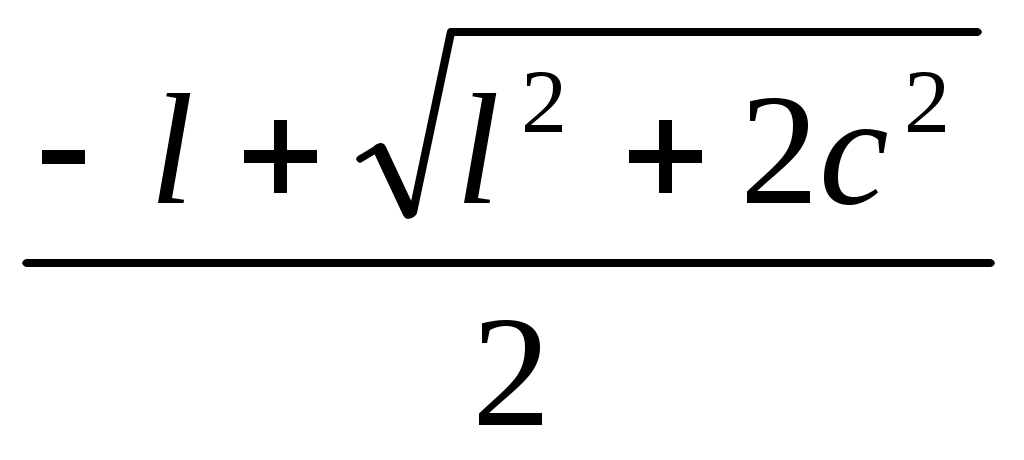

Салу: 1) АВ = с кесіндісі

2)  (О,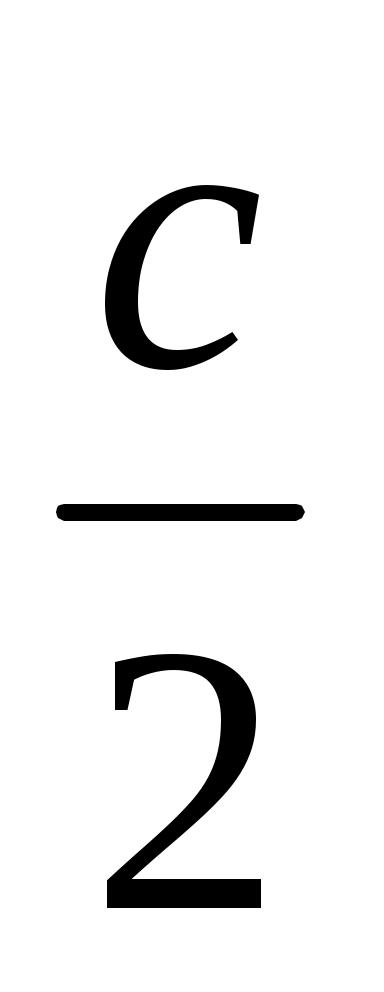 ) шеңбері, мұнда О  АВ және ОА = ОВ

3) ОК – АВ кесіндісінің орта перпендикуляры

4) Е = OK   (О,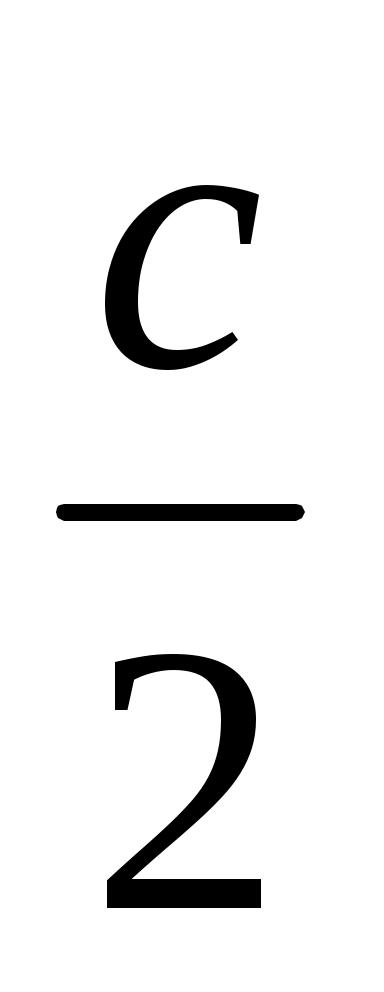 ) нүктесі

5) р =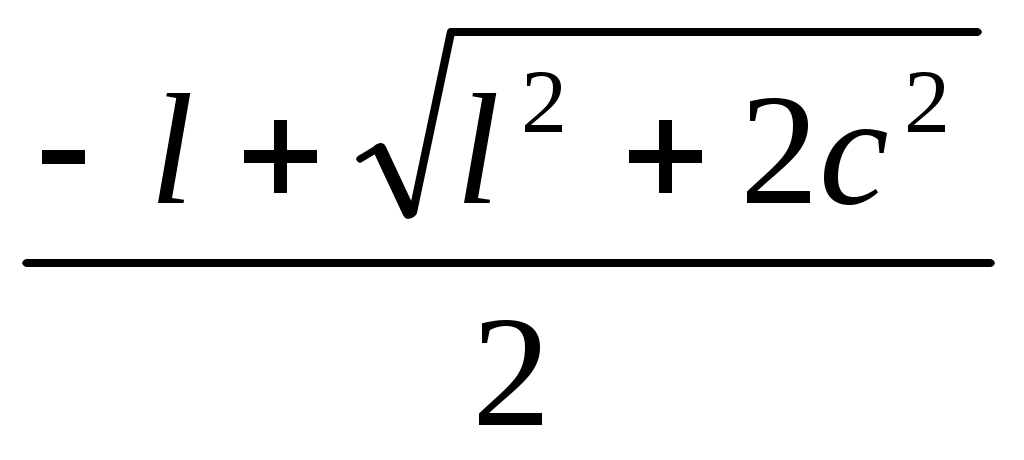 кесіндісі (3.1., ІХ, ІІ және ІV салулар)

6) ₁ (Е, р) шеңбері

7) D = АВ  ₁ нүктесі

8) ЕD түзуі

9) С = ED   (О,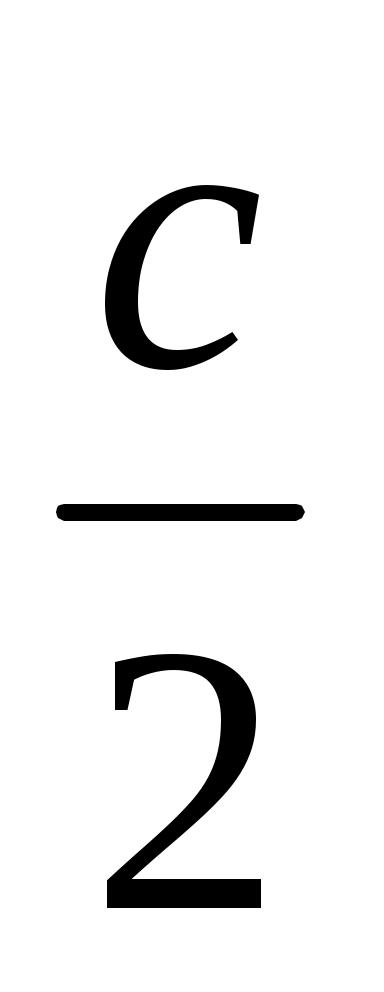 ) нүктесі

10) СА, СВ кесінділері

АВС – ізделінді.

Зерттеу: Егер l 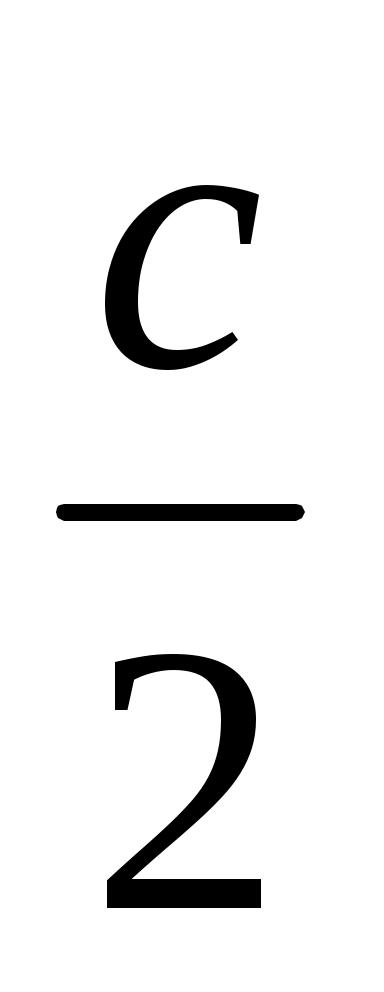 болса, есептің екі шешімі бар; l = 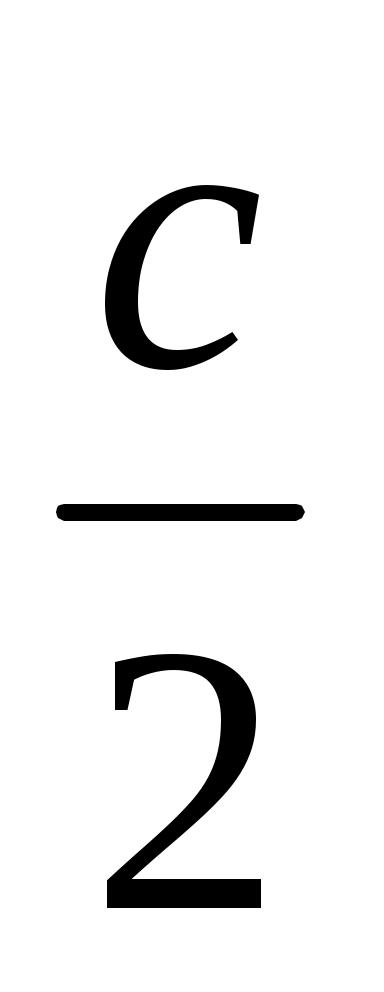- бір шешімі бар; l 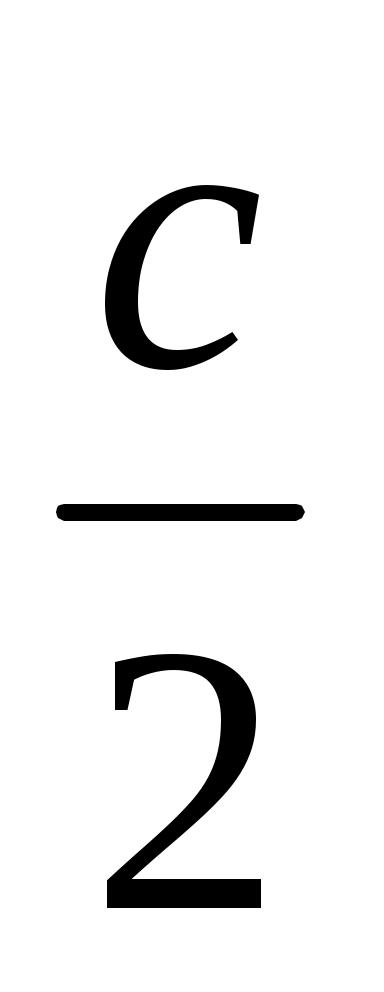 - шешімі жоқ.

Есеп 4: Ұзындықтары а, в, с және d болатын кесінділер берілген.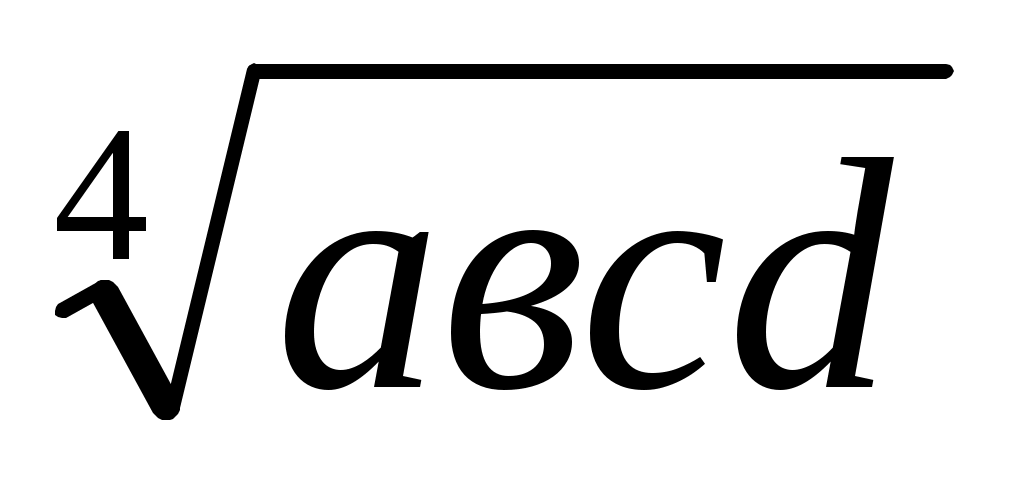 формуласымен өрнектелетін кесіндінің ұзындығын табыңыз.

---

Шешуі: Төрт кесіндінің көбейтінділерінен төртінші дәрежелі түбірді мына түрде жазуға болады:

=

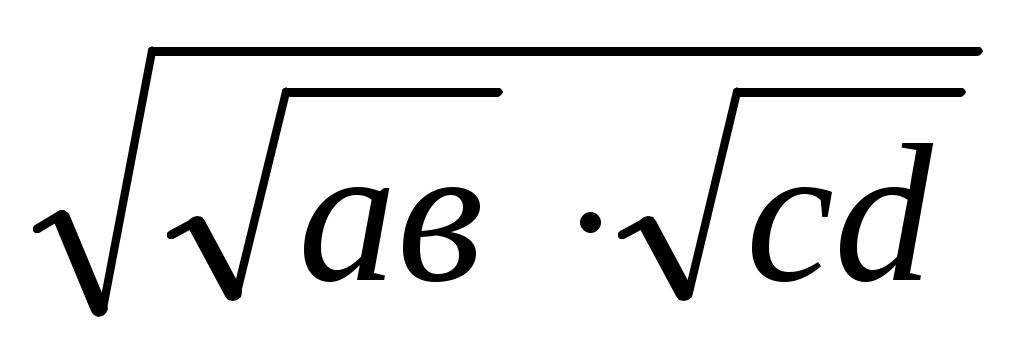
Екі кесіндінің пропорционал ортасын салу белгілі болғандықтан (3.1., VІІІ салу), алдымен ұзындығы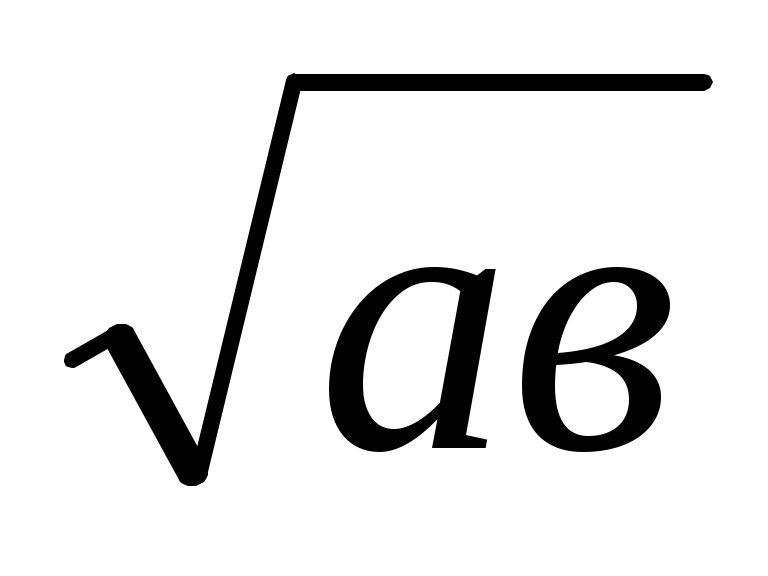 болатын х₁ кесіндісін, содан соң ұзындығы 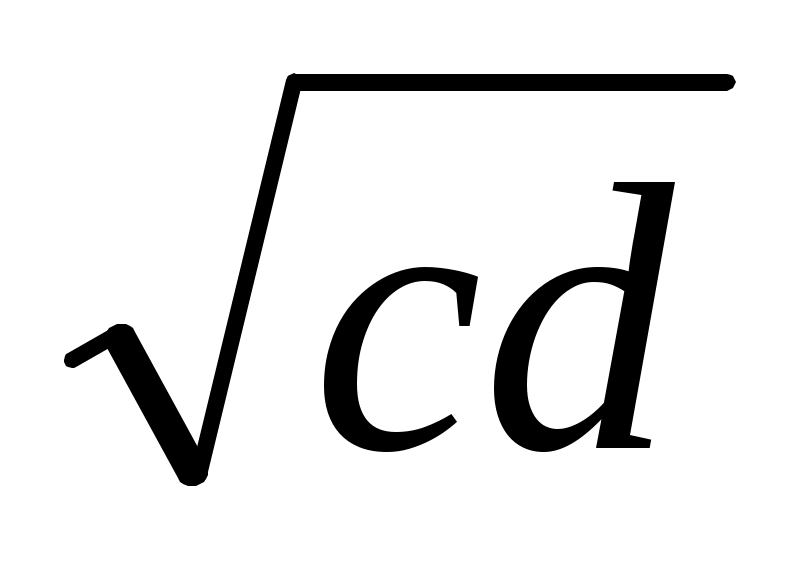болатын х₂ кесіндісін салып аламыз. Сонда ізделінді кесіндінің ұзындығы болады.

Есеп 5: Ұзындықтары а, в, с болатын кесінділер берілген. Ұзындығы

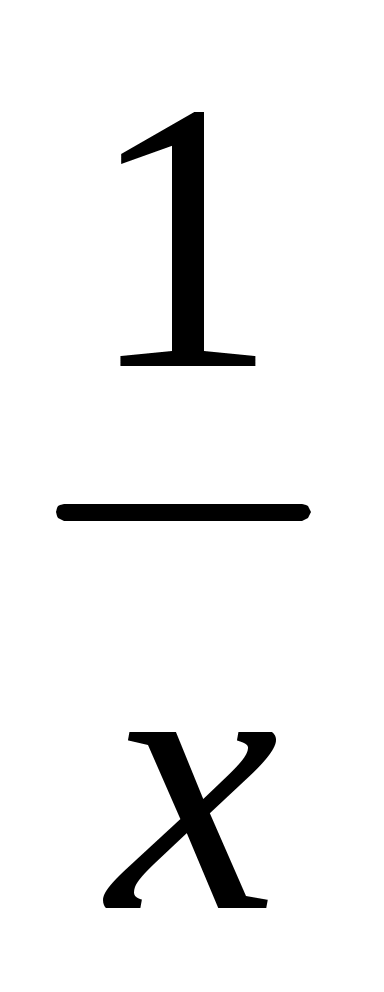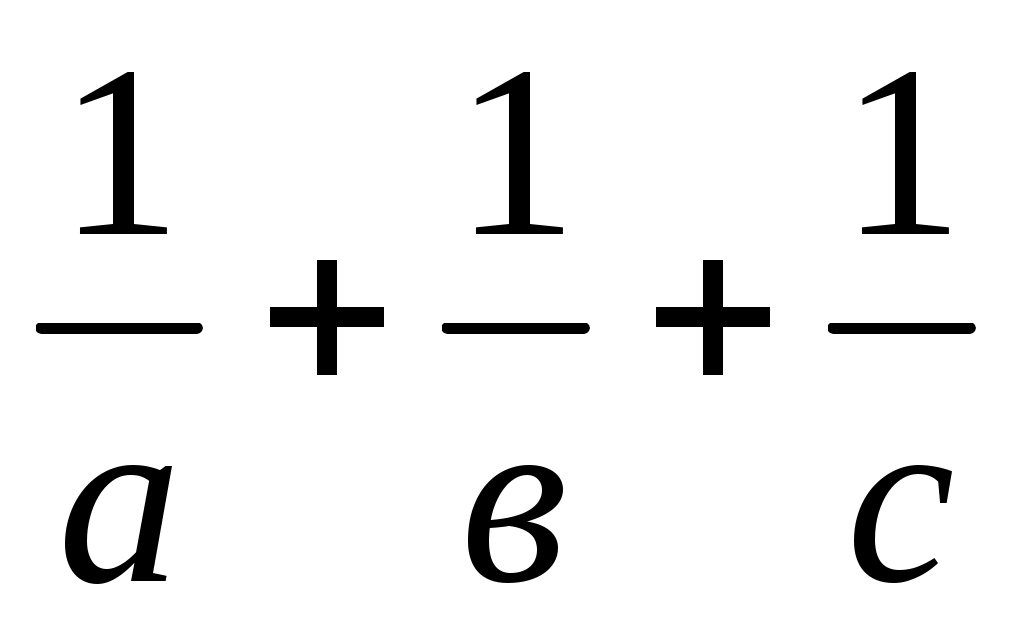= формуласымен өрнектелетін х кесіндісін салыңыз.

Шешуі: Алдымен ұзындығы

= (*)

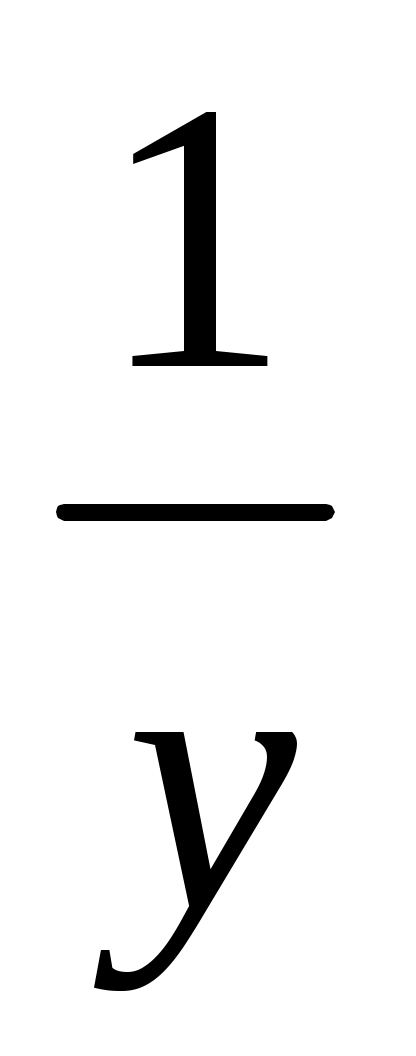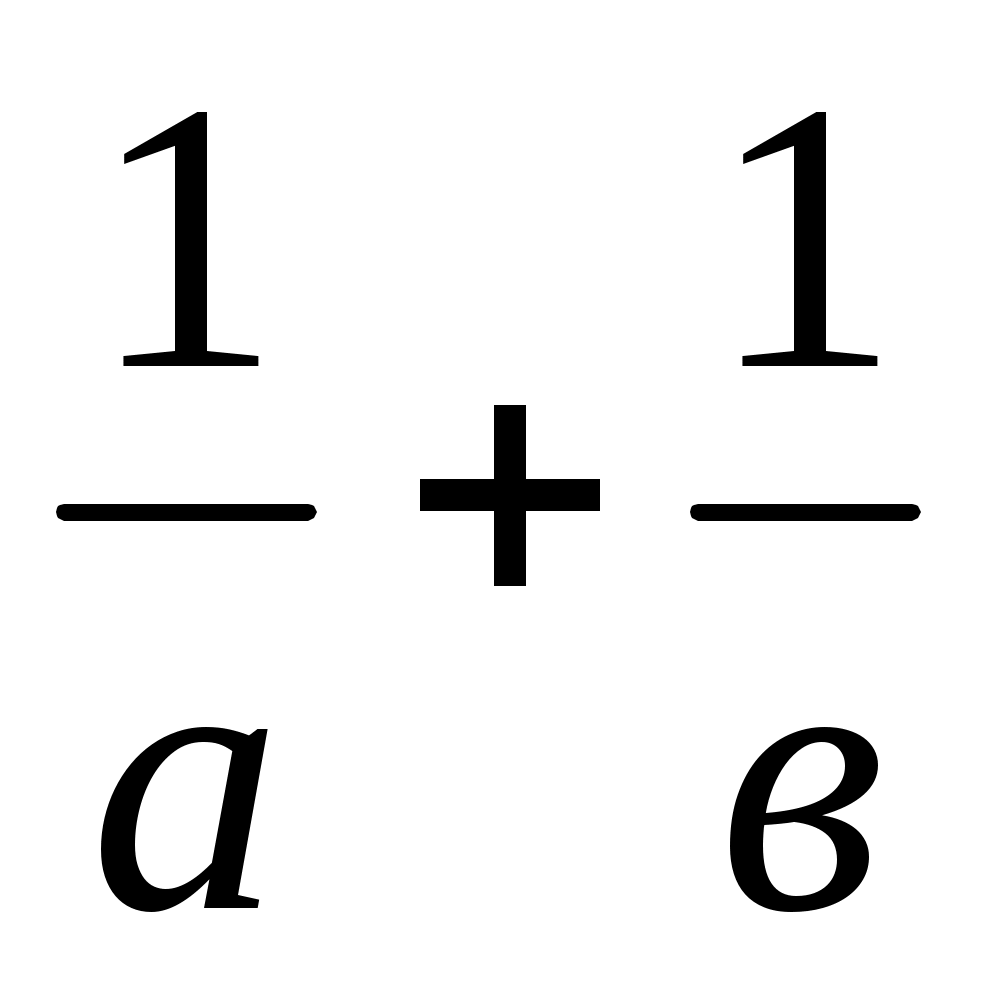формуласымен өрнектелетін у кесіндісін салып аламыз. Ол үшін (*) теңдігін

=

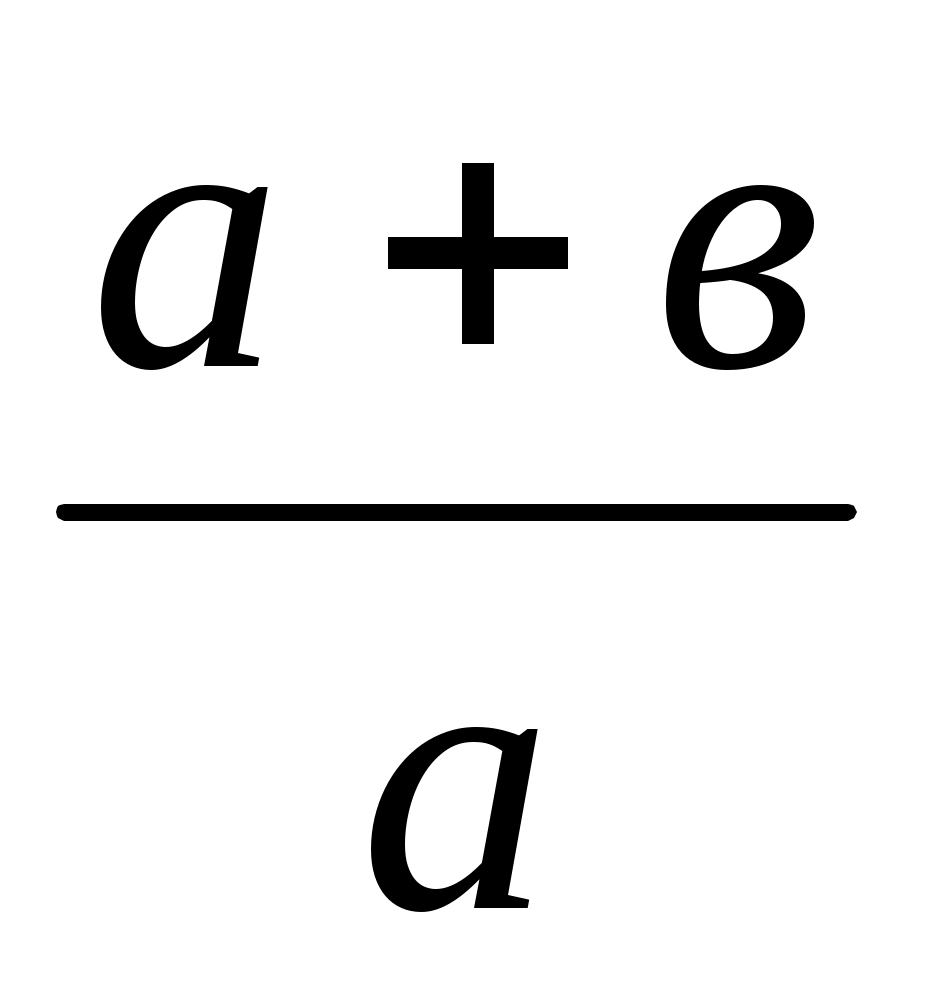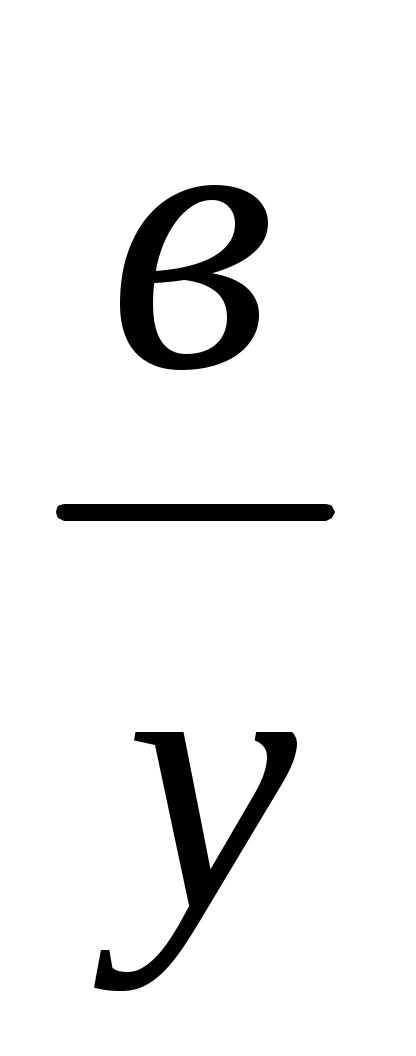
түріне келтіреміз, сонда у кесіндісі а + в, а, в кесінділеріне пропорционал төртінші кесінді болады (3.1., VІ салу). у кесіндісі салынған соң, х те дәл осылайша тұрғызылады.

=

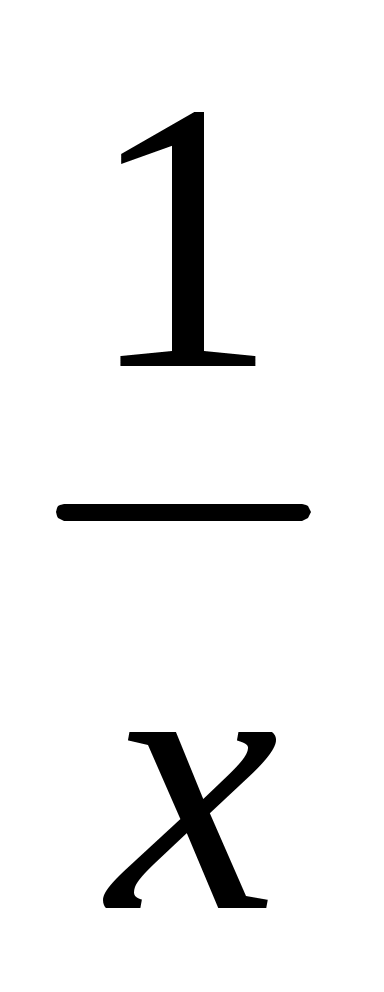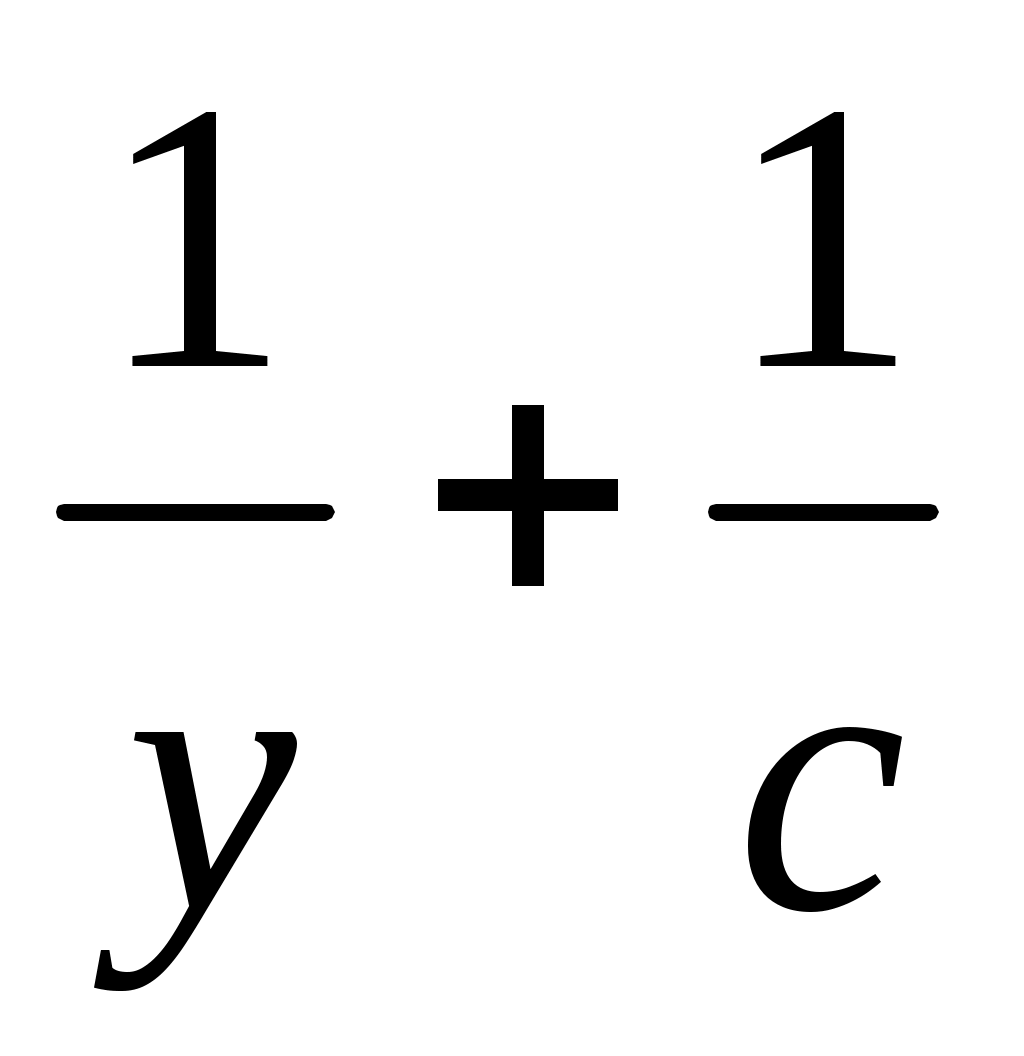
Формуласы бойынша х кесіндісі у + с, у, с кесінділеріне пропорционал төртінші кесінді.



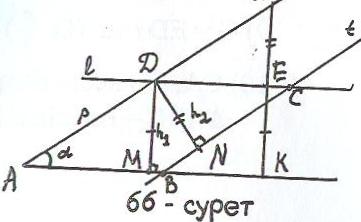
Есеп 6: h₁, h₂ биіктіктері және 2р периметрі бойынша параллелограмм салыңыз.

Шешуі:

Талдау: Есеп шешілді делік, АВСD – ізделінді

параллелограмм (66–сурет). АВ=х деп белгілеп

алайық, ВС = р – х.

S = h₁  AB = h₁  xжәне S = h ₂  BС = h₂  (

---

Смотрите также файлы

• Природные пожары.docx

• Практическая работа к теме Семья традиции Тема занятия Тема Моя семья традиции и ценности Класс 2.docx

• Тжірибелік сабаа арналан тапсырмалар Фт заттар мен энергия алмасу Тапсырма1. Анытама берііз Заттар мен энергия алмасу дегеніміз.docx

• Общий объем аудиторной работы обучающихся с овз в случае увеличения срока обучения на один год не может составлять менее 6018 академических часов за шесть учебных лет.docx

• Введение Открытие предприятия по производству детской игровой мебели из картона с целью выхода на новый сегмент рынка детской мебели и игрушек и получения прибыли.docx