Файл: Мазмны Кiрiспе 1 тарау. Геометриялы салулар теориясыны кейбiр мселелерi 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 220
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
р – x)
Бұл теңдіктердің оң жақтарын теңестіріп,
h1 x = h2 (р – x) x =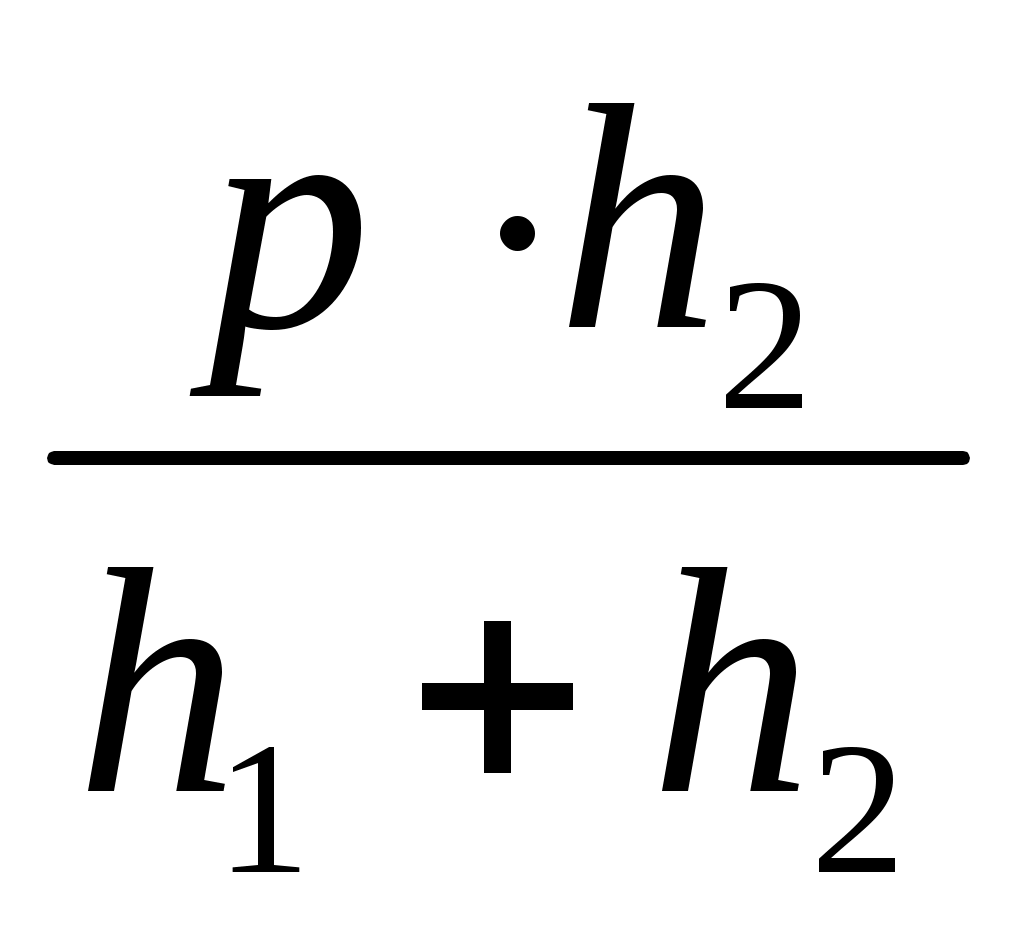
теңдігі шығады. Ал бұл кесіндіні алгебралық әдіс арқылы салуға болады (3.1., VІ салу). Егер DAB = деп параллелограмның сүйір бұрышын белгілесек, онда ADM, CDN (M, N– биіктіктердің табандары) үшбұрыштарынан
AD =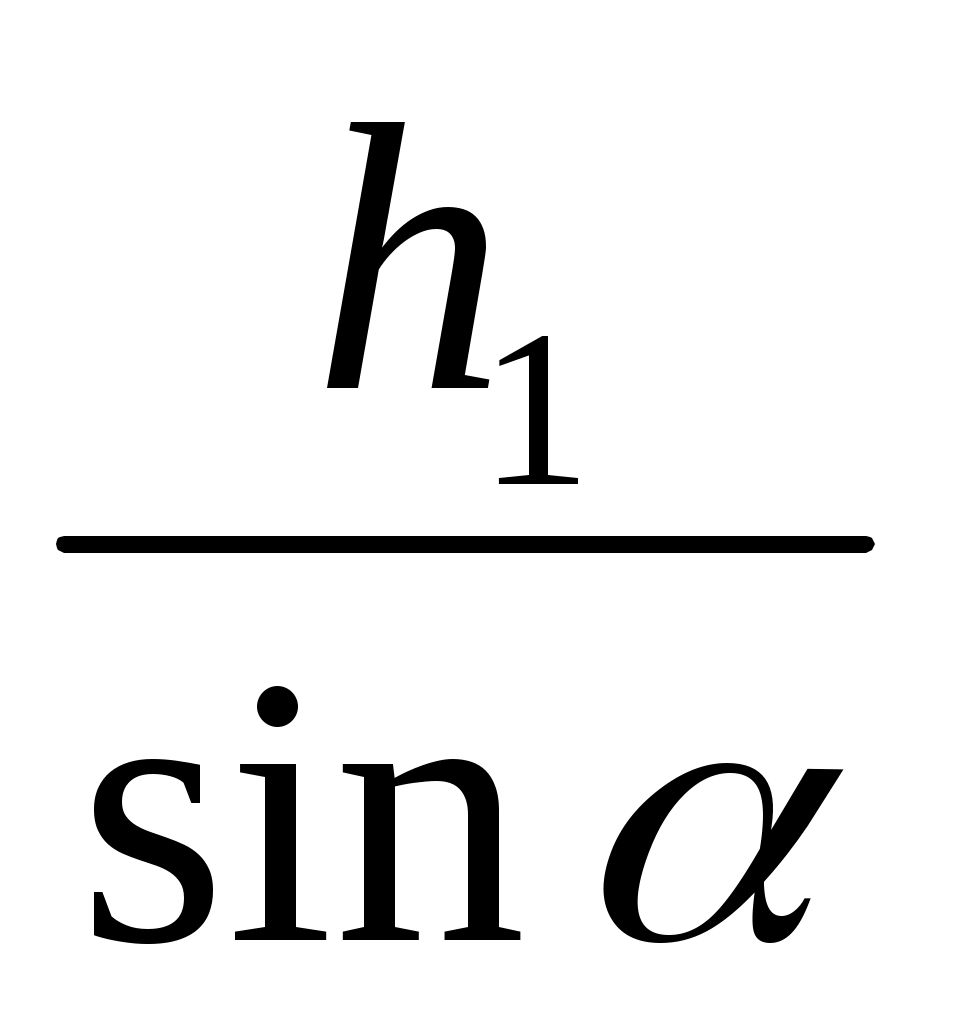
, CD =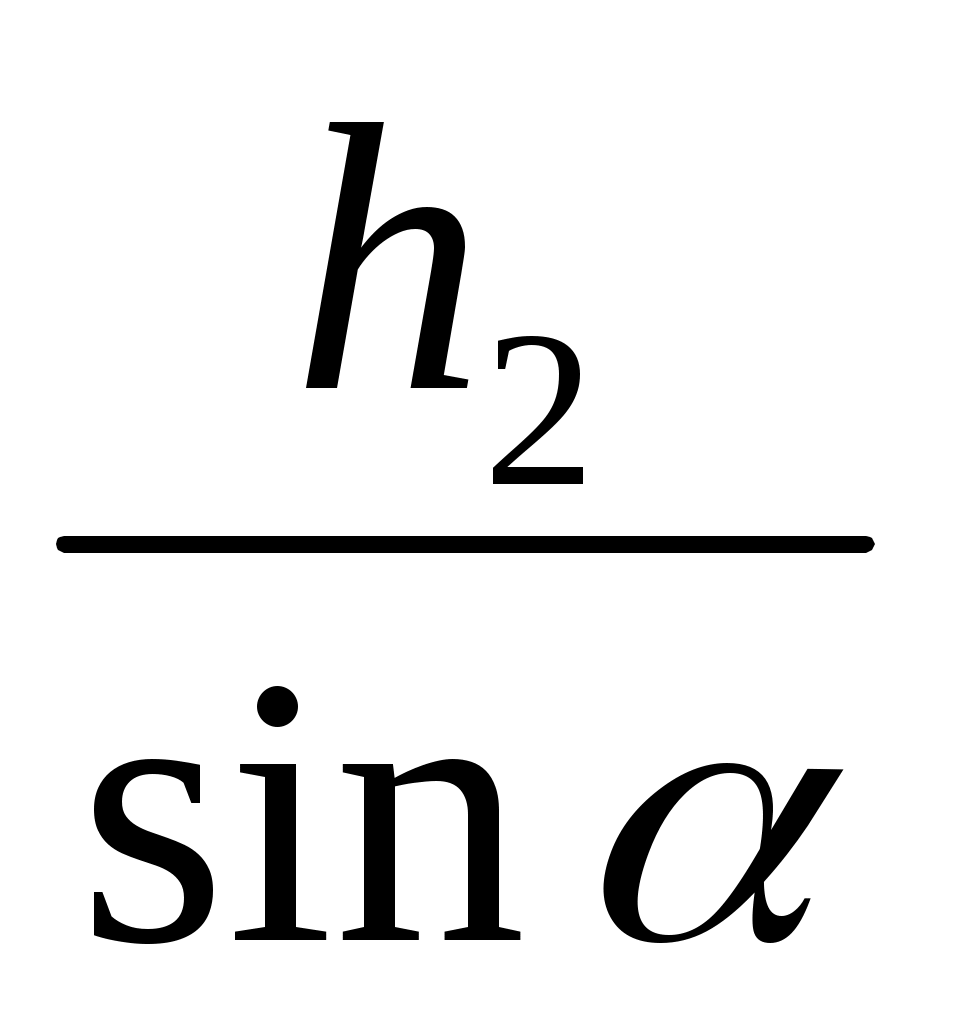 
теңдіктері шығады.
AD + CD = p sin =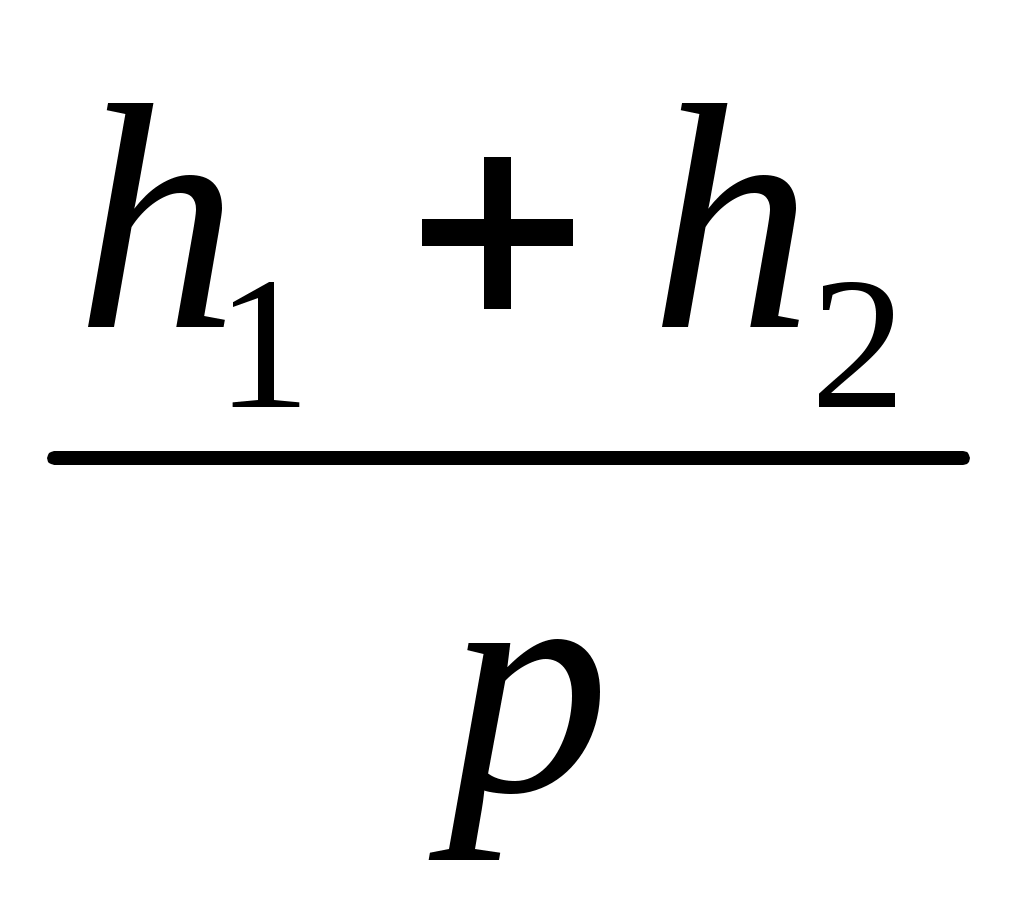
(**)
(**) бұрышын р гипотенузасы, h1, h2 катеті бойынша тұрғызылған тікбұрышты үшбұрыштың берілген катетке қарсы жатқан бұрыш ретінде салуға болады.
Салу: 1) h1 + h2 кесіндісі
2) AKL тікбұрышты үшбұрышы (KL = h1+ h2 катет, AL = p гипотенуза)
3) АК түзуі
4) КЕ = h1 кесіндісі (К – Е – L қатынасы орындалады)
5) Е нүктесі арқылы l АВ түзуі
6) D = l AL нүктесі
7) DC =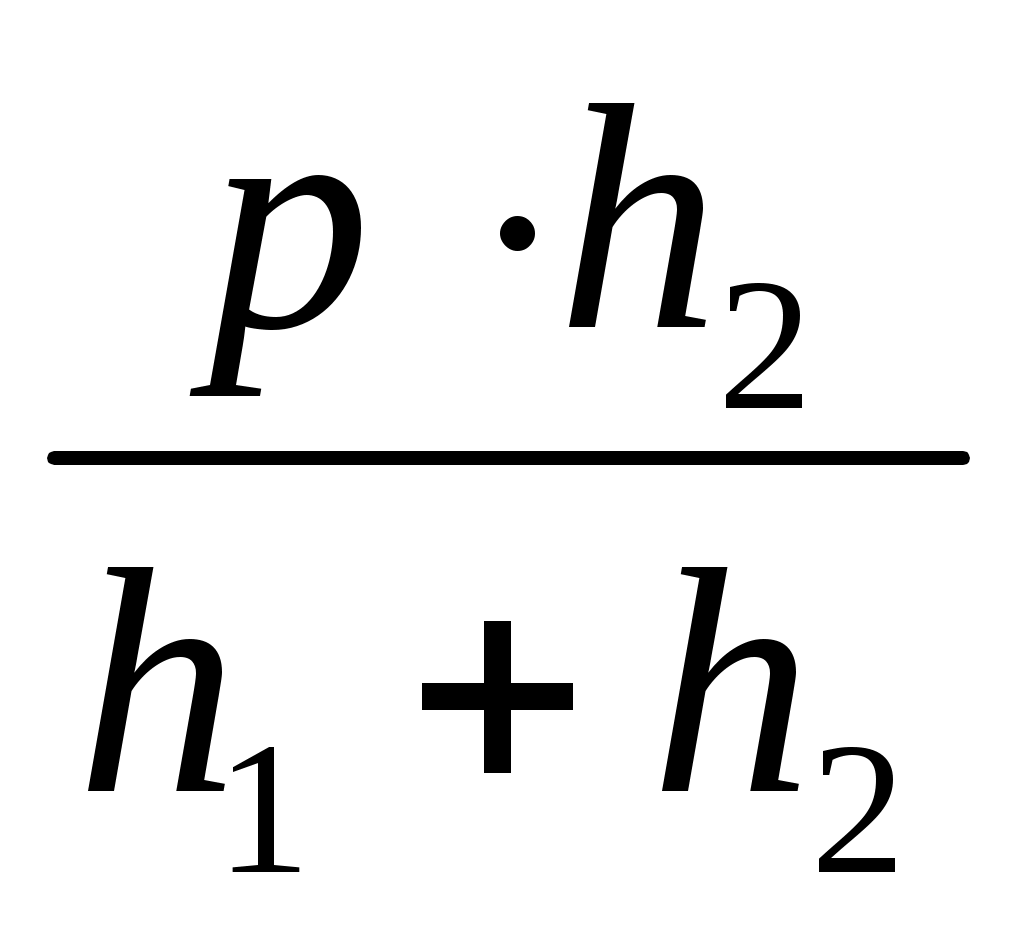 кесіндісі (С l және D – E – C ) (3.1., VI салу)
8) С нүктесі арқылы t АВ түзуі
9) B = t AL нүктесі
АВСD – ізделінді параллелограмм
Дәлелдеу: D ED, ED AK және EK = h1 болғандықтан, DM = h1.
DN = DC sin =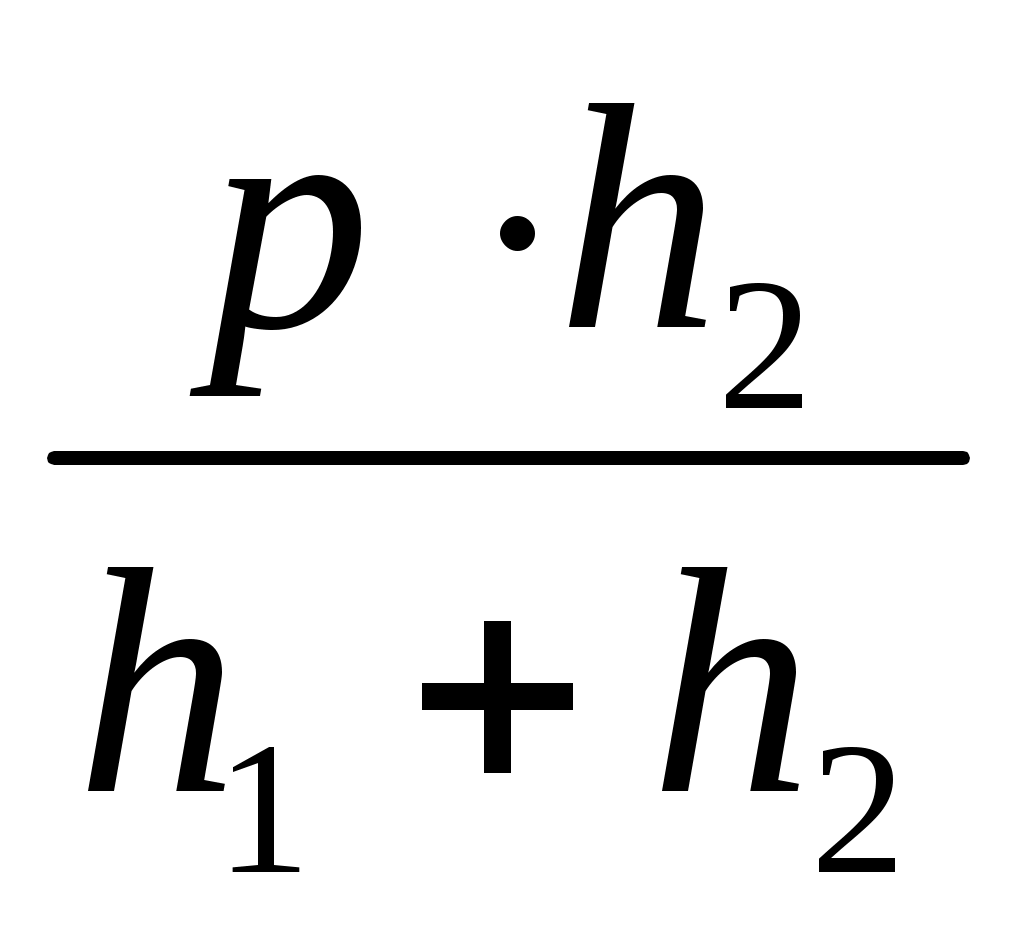 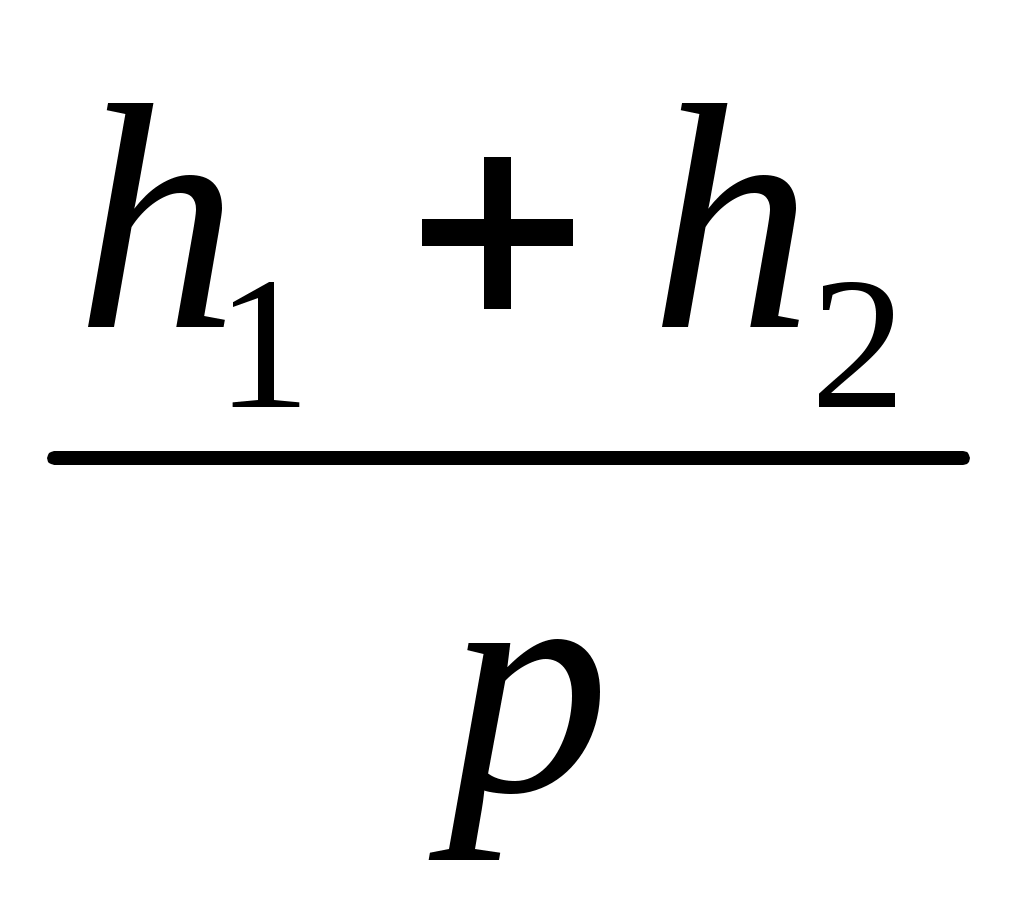= h2, яғни DN = h2.
DL = h2 sin = DC p = AD + DL = AD + DC.
Зерттеу: h1 + h2 р теңсіздігі орындалғанда ғана ALK тікбұрышты үшбұрышын салуға болады. Қалған салу қадамдары бірмәнді орындалады. Демек, h1 + h2 р қатынасында есептің шешімі бар және ол біреу ғана.
§4. Инверсия әдісі
OQM. Олай болса,
= 
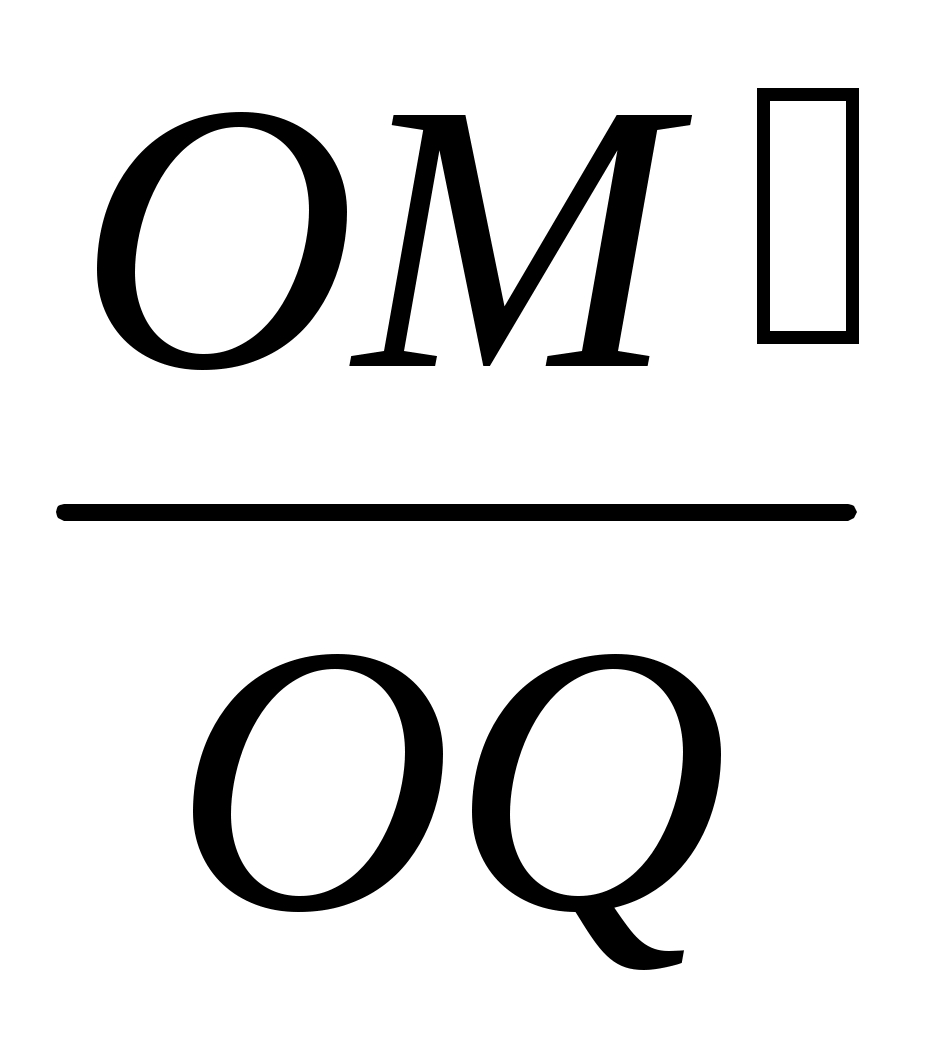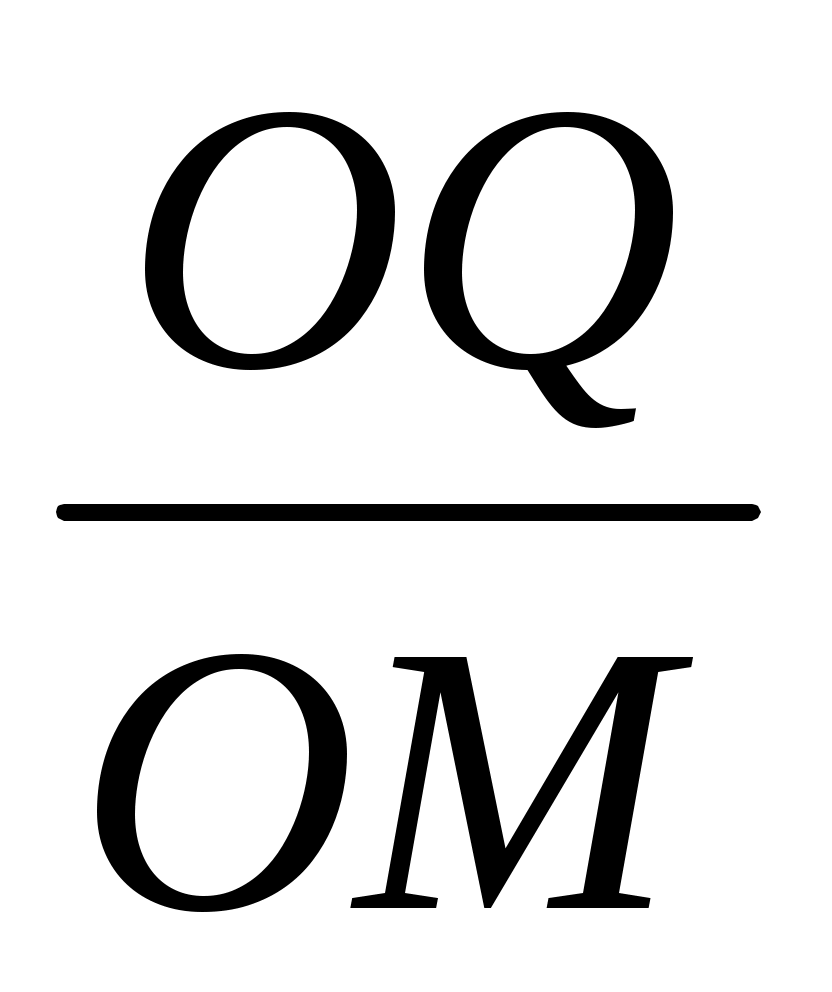, яғни ОМ' ОМ = OQ2 = R2.
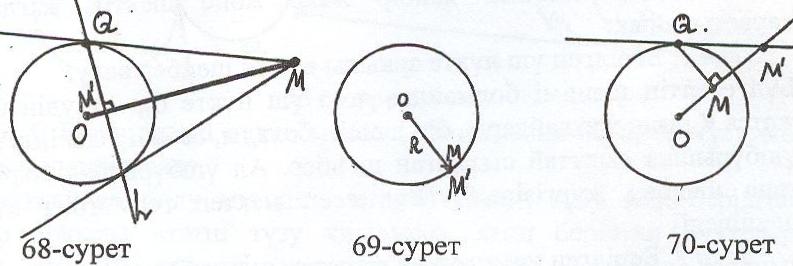
2 – жағдай. М — шеңберінің бойындағы нүкте, яғни М (69 – сурет). Бұл жағдайда М нүктесінің образы осы нүктенің өзі болады. Себебі
ОМ ОМ' = RR = R2.
3 – жағдай. М — шеңберінің сыртындағы нүкте (70 – сурет). Бұл жағдайда инверсияның бірмәнділігін ескеріп, салуды керісінше тәртіппен орындаймыз.
4.3. Салу есептерін инверсия әдісімен шешкенде
қолданылатын теоремалар
Теорема1: Инверсия центрі арқылы өтетін шеңбер инверсияда түзуге көшеді және бұл түзу инверсия центрі мен берілген шеңбердің центрлері арқылы өтетін түзуге перпендикуляр болады.
Теорема2: Инверсия центрі арқылы өтпейтін шеңбер инверсияда шеңберге көшеді.
Теорема3: Инверсия центрі арқылы өтпейтін түзу инверсияда шеңберге көшеді және ол шеңбер инверсия центрі арқылы өтеді.
Теорема4: Егер шеңбер өзара инверсиялы екі нүкте арқылы өтсе, онда инверсияда бұл шеңбер өзіне көшеді.
Теорема5: Егер 1, 2 сызықтары бір – бірінен инверсия центрінен өзге М нүктесінде жанасса, онда олардың образдары М' = f (М) нүктесінде жанасады. Мұнда 1 – шеңбер немесе түзу, ал 2 – шеңбер.
Теорема 6: Базистік шеңберден өзге шеңбер инверсияда өз - өзіне көшу үшін, оның базис шеңберге ортогональ болуы қажет және жеткілікті.
(Екі шеңбер ортогональ деп аталады, егер олар тікбұрыш жасай қиылысса, яғни олардың қиылысу нүктесінен жүргізілген радиустары өзара перпендикуляр болса.)
4.4. Аполлоний есебі
Инверсия әдісімен, жалпы жағдайда, Аполлоний есебі шешіледі. Аполлоний есебі: берілген үш шеңбермен жанасатын шеңбер салу. Бұл есепті ең алғаш б.э.д. ІІІ ғасырда атақты грек геометрі Аполлоний Пергский шешкен. Бірақ оның еңбектері бізге дейін жеткен жоқ, ол туралы тек ежелгі математиктер, мысалы Паппның айтуы бойынша білеміз. Бұл есепті Аполлонийдің қалай шешкендігі де белгісіз.
Мектептегі геометрия курсында кездесетін шеңберге қатысты салу есептері – осы Аполлоний есебінің жеке және шектік жағдайлары болып табылады. Жеке жағдайлар берілген шеңберлердің орналасуына байланысты болса, шектік жағдайлар барлық немесе кейбір берілген шеңберлердің нүктеге (егер шеңбердің радиусы шексіз кемісе) және түзуге (егер шеңбердің радиусы шексіз өссе) айналуына байланысты болады.
Аполлоний есебінің кейбір жеке және шектік жағдайларын қарастырайық:
Есеп 1. Берілген үш нүкте арқылы өтетін шеңбер салу.
Бұл есептің шешімі болмайды, егер үш нүкте бір түзудің бойында жатса. Қалған жағдайларда бір шешім болады, себебі ізделінді шеңбер – үшбұрышқа сырттай сызылған шеңбер. Ал үшбұрышқа сырттай бір ғана шеңбер жүргізіледі. (Бұл есеп мектеп геометрия курсында шешіледі)
Есеп 2. Берілген үш түзумен жанасатын шеңбер салу.
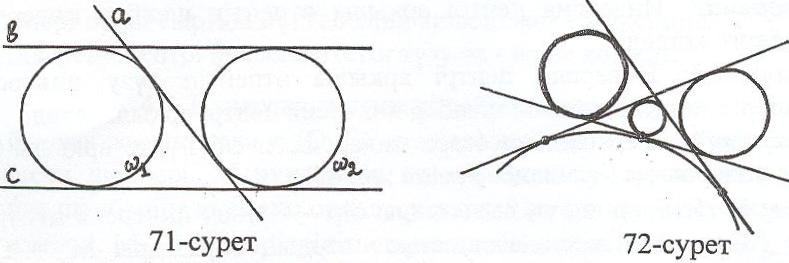
Есептің шешіміне қатысты төмендегі жағдайлар болу мүмкін: егер берілген үш түзу өзара параллель орналасқан болса, онда есептің шешімі болмайды; егер түзулердің екеуі өзара параллель, ал үшіншісі оларды қиса, онда септің екі шешімі болады (71-сурет); егер түзулер қос – қостан қиылысса, онда есептің төрт шешімі болады (72-сурет).
Есеп 3. Берілген нүкте арқылы өтіп, берілген екі параллель түзулермен жанасатын шеңбер салу.
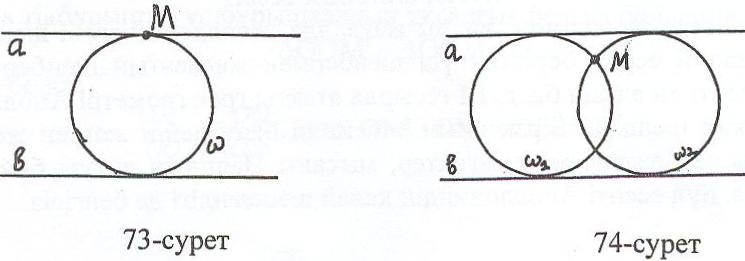
Бұл есептің шешіміне қатысты мына жағдайлар болу мүмкін: егер берілген нүкте берілген түзулермен шектелген жолақтан тысқары жатса, есептің шешімі болмайды; егер берілген нүкте берілген түзулердің бірінде жатса, онда есептің бір ғана шешімі болады (73-сурет); егер берілген нүкте берілген түзулермен шектелген жолаққа тиісті болса, онда есептің екі шешімі болады (74-сурет).
Есеп 4. Берілген нүкте арқылы өтіп, берілген екі қиылысатын түзулерді жанайтын шеңбер салу.
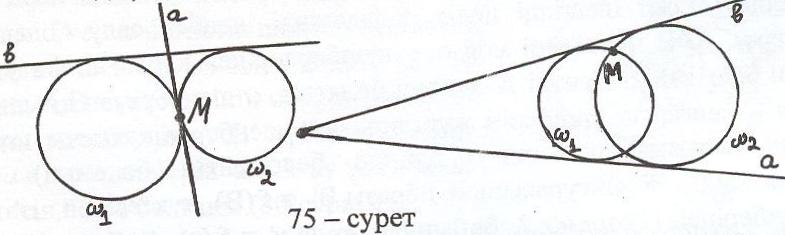
Егер нүкте берілген түзулердің қиылысу нүктесі болса, онда есептің шешімі болмайды; қалған жағдайларда есептің екі шешімі бар (75-сурет).
Есеп 5. Берілген екі нүкте арқылы өтетін және берілген түзумен жанасатын шеңбер салу.
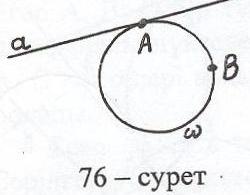
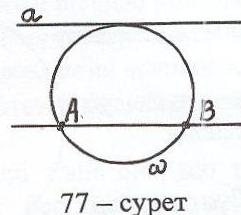
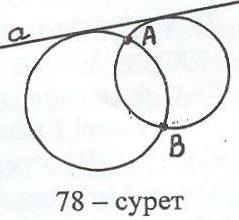
Мына жағдайлар болу мүмкін: егер берілген түзу мен берілген нүктелер арқы-лы өтетін түзу қиылысса, яғни берілген нүктелер берілген түзудің әртүрлі жағында орналасса, есептің шешімі болмайды, сонымен қатар берілген нүкте-лер берілген түзуге тиісті болған жағдайда да есептің шешімі жоқ; егер беріл-ген нүктелердің біреуі берілген түзуге тиісті (76-сурет) немесе берілген нүкте-лер арқылы өтетін түзу берілген түзуге параллель (77-сурет) болса, есептің бір ғана шешімі болады; қалған жағдайда септің екі шешімі бар (78-сурет).
Есеп 6. Берілген үш шеңбермен жанасатын шеңбер салу.
Бұл есептің шешулерінің саны берілген шеңберлердің орналасу жағдайларына байланысты болады. Осы жағдайлардың бірнешеуін қарастырайық:
1) Үш шеңбердің бір – бірімен ешқандай ортақ нүктесі жоқ және олар бірінің ішінде бірі орналасқан. Онда есептің шешімі болмайды.
2) Берілген екі шеңбер жанасады, ал үшіншісі оларды жанасу нүктесінде қиып өтеді. Онда есептің екі шешімі бар.
3) Егер берілген шеңберлердің әрқайсысы қалған екеуінің сыртында және әрбір екеуіне жүргізілген жанаманың үшіншісімен ортақ нүктесі болмаса, онда есептің сегіз шешімі бар.
4) Егер берілген үш шеңбер қос – қостан бір нүктеде жанасса, онда есептің шешімдерінің саны шексіз көп болады.
Аполлоний есебін шешу барысында берілген шеңберлердің орналасуына қатысты көрсетілген жағдайлардан басқа отыздан астам орналасуы болатыны табылды.
4.5. Инверсия әдісімен шешілетін салу есептеріне мысалдар
Есеп 1: (О, r) шеңбері және А , В нүктелері берілген. А, В нүктелері арқылы өтіп, шеңберін жанайтын шеңбер салыңыз.
Шешуі:
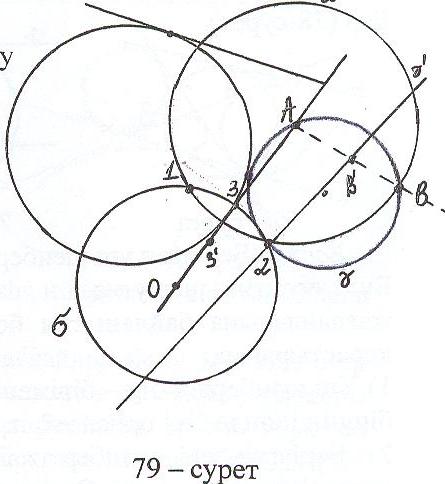
Талдау: Есеп шешілді делік, ізделінді шеңбер салу болсын (79-сурет). А, В нүктелері мен , шеңберлерінен құралған фигураны Ғ деп белгілейік. Центрі А нүктесі болатын, шеңберімен қиылысатын кез – келген шеңберін жүргізіп, осы шеңберге қатысты инверсия қарастырамыз (алда оны f түрінде белгілейтін боламыз). Сонда инверсияда Ғ фигурасының образы В' = f (В) нүктесінен, ' = f () шеңберінен (Теорема 2 бойынша) және ' = f () түзуінен (Теорема1 бойынша) құралған қандай да бір Ғ' фигурасы болады. А – инверсия центрі, сондықтан оның образы болмайды. Олай болса, Теорема5 бойынша ' түзуі ' шеңберімен жанасады. Ғ' фигурасын салу оңай, себебі В', ' – берілген фигуралардың образдары, ал ' - В' нүктесі арқылы өтетін және ' шеңберімен жанасатын түзу. Онда f инверсиясында ' түзуінің образы болатын шеңберін Теорема3 бойынша салу оңай.
С
алу: 1) Центрі А нүктесі болатын және
шеңберімен қиылысатын кез – келген
шеңбері (81-сурет)
2) ОА түзуінің шеңберімен қиылысу
Бұл теңдіктердің оң жақтарын теңестіріп,
h1 x = h2 (р – x) x =
теңдігі шығады. Ал бұл кесіндіні алгебралық әдіс арқылы салуға болады (3.1., VІ салу). Егер DAB = деп параллелограмның сүйір бұрышын белгілесек, онда ADM, CDN (M, N– биіктіктердің табандары) үшбұрыштарынан
AD =
, CD = теңдіктері шығады.
AD + CD = p sin =
(**)(**) бұрышын р гипотенузасы, h1, h2 катеті бойынша тұрғызылған тікбұрышты үшбұрыштың берілген катетке қарсы жатқан бұрыш ретінде салуға болады.
Салу: 1) h1 + h2 кесіндісі
2) AKL тікбұрышты үшбұрышы (KL = h1+ h2 катет, AL = p гипотенуза)
3) АК түзуі
4) КЕ = h1 кесіндісі (К – Е – L қатынасы орындалады)
5) Е нүктесі арқылы l АВ түзуі
6) D = l AL нүктесі
7) DC =
кесіндісі (С l және D – E – C ) (3.1., VI салу)8) С нүктесі арқылы t АВ түзуі
9) B = t AL нүктесі
АВСD – ізделінді параллелограмм
Дәлелдеу: D ED, ED AK және EK = h1 болғандықтан, DM = h1.
DN = DC sin =
= h2, яғни DN = h2.DL = h2 sin = DC p = AD + DL = AD + DC.
Зерттеу: h1 + h2 р теңсіздігі орындалғанда ғана ALK тікбұрышты үшбұрышын салуға болады. Қалған салу қадамдары бірмәнді орындалады. Демек, h1 + h2 р қатынасында есептің шешімі бар және ол біреу ғана.
§4. Инверсия әдісі
Салу есептерін шешудің тағы бір әдісі – инверсия әдісі. Бұл әдістің көмегімен әлдеқайда қиынырақ салу есептері шешіледі. Инверсия әдісі басқа әдістерге қарағанда кейінірек пайда болған және оның қиындығы – көп салулар орындау қажеттілігінде.
4.1. Инверсияның анықтамасы, қарапайым қасиеттері.
Айталық жазықтықта (О, R) шеңбері берілген.
А
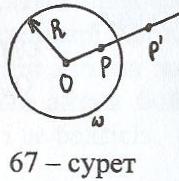
нықтама: Жазықтықтың О нүктесінен өзге кез – келген Р нүктесіне мына шарттарды:
1) Р' [ОР)
2) ОР ОР' = R2
қанағаттандыратындай Р' нүктесін сәйкес қоятын жазықтық түрлендіруін инверсия деп атайды (67-сурет). Мұндағы Р' - шеңберіне қатысты Р нүктесіне кері немесе инверсиялы нүкте, - базистік шеңбер, О – инверсия центрі, R – инверсия радиусы.
Анықтамадан, егер инверсияда Р нүктесіне Р' нүктесі сәйкес келсе, онда, керісінше, Р' нүктесіне Р нүктесі сәйкес келетінін көреміз. Олай болса, инверсия - өзара бірмәнді түрлендіру.
Инверсияның қарапайым қасиеттері:
10. Егер Р' нүктесі Р нүктесіне инверсиялы болса, онда, керісінше, Р нүктесі Р' нүктесіне инверсиялы болады.
20. Егер инверсияда Ф фигурасы Ф' фигурасына түрленсе, онда Ф' фигурасы Ф фигурасына түрленеді.
30. Жазықтықтың ешбір нүктесі инверсия центріне инверсиялы нүкте болмайды.
40. Базистік шеңбердің әрбір нүктесі өз - өзіне инверсиялы болады.
50. Егер берілген нүкте базистік шеңбердің сыртында жатса, онда оған инверсиялы нүкте оның ішінде жатады және керісінше.
60. Базистік шеңбердің сыртындағы нүкте одан шексіз алыстаған сайын, оған инверсиялы нүкте инверсия центріне шексіз жақындайды. Керісінше сөйлем дұрыс болады.
70. Инверсия центрінен шығатын сәуле инверсияда өз - өзіне түрленеді (көшеді) және де базистік шеңберге қатысты сәуленің ішкі нүктелері оның сыртқы нүктелеріне көшеді және керісінше.
80. Инверсия центрі арқылы өтетін түзу өз - өзіне көшеді.
4.2. Инверсияда нүктенің образын тұрғызу
Айталық жазықтықта (О, R) шеңбері және М нүктесі берілген. ин-версия шеңбері болсын. М нүктесінің инверсиядағы образын табу үшін, оның шеңберіне қатысты орналасу жағдайларын қарастырайық:
1 – жағдай. М — шеңберінің сыртындағы нүкте (68 – сурет). Онда салу жоспары төмендегіше болады:
1) [ОМ) сәулесін жүргіземіз
2) М нүктесі арқылы шеңберіне жанама
3) Осы жанаманың шеңберімен қиылысу нүктесін Q делік
4) Q нүктесінен [ОМ) сәулесіне перпендикуляр: h
5) M' = h [ОМ) нүктесі
М' – ізделінді нүкте.
Шынында да, MQ шеңберіне жанама болғандықтан, OQM = 900. Сонда тікбұрышты үшбұрыштардың ұқсастық белгісі бойынша OQM'
OQM. Олай болса,
= , яғни ОМ' ОМ = OQ2 = R2.2 – жағдай. М — шеңберінің бойындағы нүкте, яғни М (69 – сурет). Бұл жағдайда М нүктесінің образы осы нүктенің өзі болады. Себебі
ОМ ОМ' = RR = R2.
3 – жағдай. М — шеңберінің сыртындағы нүкте (70 – сурет). Бұл жағдайда инверсияның бірмәнділігін ескеріп, салуды керісінше тәртіппен орындаймыз.
4.3. Салу есептерін инверсия әдісімен шешкенде
қолданылатын теоремалар
Теорема1: Инверсия центрі арқылы өтетін шеңбер инверсияда түзуге көшеді және бұл түзу инверсия центрі мен берілген шеңбердің центрлері арқылы өтетін түзуге перпендикуляр болады.
Теорема2: Инверсия центрі арқылы өтпейтін шеңбер инверсияда шеңберге көшеді.
Теорема3: Инверсия центрі арқылы өтпейтін түзу инверсияда шеңберге көшеді және ол шеңбер инверсия центрі арқылы өтеді.
Теорема4: Егер шеңбер өзара инверсиялы екі нүкте арқылы өтсе, онда инверсияда бұл шеңбер өзіне көшеді.
Теорема5: Егер 1, 2 сызықтары бір – бірінен инверсия центрінен өзге М нүктесінде жанасса, онда олардың образдары М' = f (М) нүктесінде жанасады. Мұнда 1 – шеңбер немесе түзу, ал 2 – шеңбер.
Теорема 6: Базистік шеңберден өзге шеңбер инверсияда өз - өзіне көшу үшін, оның базис шеңберге ортогональ болуы қажет және жеткілікті.
(Екі шеңбер ортогональ деп аталады, егер олар тікбұрыш жасай қиылысса, яғни олардың қиылысу нүктесінен жүргізілген радиустары өзара перпендикуляр болса.)
4.4. Аполлоний есебі
Инверсия әдісімен, жалпы жағдайда, Аполлоний есебі шешіледі. Аполлоний есебі: берілген үш шеңбермен жанасатын шеңбер салу. Бұл есепті ең алғаш б.э.д. ІІІ ғасырда атақты грек геометрі Аполлоний Пергский шешкен. Бірақ оның еңбектері бізге дейін жеткен жоқ, ол туралы тек ежелгі математиктер, мысалы Паппның айтуы бойынша білеміз. Бұл есепті Аполлонийдің қалай шешкендігі де белгісіз.
Мектептегі геометрия курсында кездесетін шеңберге қатысты салу есептері – осы Аполлоний есебінің жеке және шектік жағдайлары болып табылады. Жеке жағдайлар берілген шеңберлердің орналасуына байланысты болса, шектік жағдайлар барлық немесе кейбір берілген шеңберлердің нүктеге (егер шеңбердің радиусы шексіз кемісе) және түзуге (егер шеңбердің радиусы шексіз өссе) айналуына байланысты болады.
Аполлоний есебінің кейбір жеке және шектік жағдайларын қарастырайық:
Есеп 1. Берілген үш нүкте арқылы өтетін шеңбер салу.
Бұл есептің шешімі болмайды, егер үш нүкте бір түзудің бойында жатса. Қалған жағдайларда бір шешім болады, себебі ізделінді шеңбер – үшбұрышқа сырттай сызылған шеңбер. Ал үшбұрышқа сырттай бір ғана шеңбер жүргізіледі. (Бұл есеп мектеп геометрия курсында шешіледі)
Есеп 2. Берілген үш түзумен жанасатын шеңбер салу.
Есептің шешіміне қатысты төмендегі жағдайлар болу мүмкін: егер берілген үш түзу өзара параллель орналасқан болса, онда есептің шешімі болмайды; егер түзулердің екеуі өзара параллель, ал үшіншісі оларды қиса, онда септің екі шешімі болады (71-сурет); егер түзулер қос – қостан қиылысса, онда есептің төрт шешімі болады (72-сурет).
Есеп 3. Берілген нүкте арқылы өтіп, берілген екі параллель түзулермен жанасатын шеңбер салу.
Бұл есептің шешіміне қатысты мына жағдайлар болу мүмкін: егер берілген нүкте берілген түзулермен шектелген жолақтан тысқары жатса, есептің шешімі болмайды; егер берілген нүкте берілген түзулердің бірінде жатса, онда есептің бір ғана шешімі болады (73-сурет); егер берілген нүкте берілген түзулермен шектелген жолаққа тиісті болса, онда есептің екі шешімі болады (74-сурет).
Есеп 4. Берілген нүкте арқылы өтіп, берілген екі қиылысатын түзулерді жанайтын шеңбер салу.
Егер нүкте берілген түзулердің қиылысу нүктесі болса, онда есептің шешімі болмайды; қалған жағдайларда есептің екі шешімі бар (75-сурет).
Есеп 5. Берілген екі нүкте арқылы өтетін және берілген түзумен жанасатын шеңбер салу.
Мына жағдайлар болу мүмкін: егер берілген түзу мен берілген нүктелер арқы-лы өтетін түзу қиылысса, яғни берілген нүктелер берілген түзудің әртүрлі жағында орналасса, есептің шешімі болмайды, сонымен қатар берілген нүкте-лер берілген түзуге тиісті болған жағдайда да есептің шешімі жоқ; егер беріл-ген нүктелердің біреуі берілген түзуге тиісті (76-сурет) немесе берілген нүкте-лер арқылы өтетін түзу берілген түзуге параллель (77-сурет) болса, есептің бір ғана шешімі болады; қалған жағдайда септің екі шешімі бар (78-сурет).
Есеп 6. Берілген үш шеңбермен жанасатын шеңбер салу.
Бұл есептің шешулерінің саны берілген шеңберлердің орналасу жағдайларына байланысты болады. Осы жағдайлардың бірнешеуін қарастырайық:
1) Үш шеңбердің бір – бірімен ешқандай ортақ нүктесі жоқ және олар бірінің ішінде бірі орналасқан. Онда есептің шешімі болмайды.
2) Берілген екі шеңбер жанасады, ал үшіншісі оларды жанасу нүктесінде қиып өтеді. Онда есептің екі шешімі бар.
3) Егер берілген шеңберлердің әрқайсысы қалған екеуінің сыртында және әрбір екеуіне жүргізілген жанаманың үшіншісімен ортақ нүктесі болмаса, онда есептің сегіз шешімі бар.
4) Егер берілген үш шеңбер қос – қостан бір нүктеде жанасса, онда есептің шешімдерінің саны шексіз көп болады.
Аполлоний есебін шешу барысында берілген шеңберлердің орналасуына қатысты көрсетілген жағдайлардан басқа отыздан астам орналасуы болатыны табылды.
4.5. Инверсия әдісімен шешілетін салу есептеріне мысалдар
Есеп 1: (О, r) шеңбері және А , В нүктелері берілген. А, В нүктелері арқылы өтіп, шеңберін жанайтын шеңбер салыңыз.
Шешуі:
Талдау: Есеп шешілді делік, ізделінді шеңбер салу болсын (79-сурет). А, В нүктелері мен , шеңберлерінен құралған фигураны Ғ деп белгілейік. Центрі А нүктесі болатын, шеңберімен қиылысатын кез – келген шеңберін жүргізіп, осы шеңберге қатысты инверсия қарастырамыз (алда оны f түрінде белгілейтін боламыз). Сонда инверсияда Ғ фигурасының образы В' = f (В) нүктесінен, ' = f () шеңберінен (Теорема 2 бойынша) және ' = f () түзуінен (Теорема1 бойынша) құралған қандай да бір Ғ' фигурасы болады. А – инверсия центрі, сондықтан оның образы болмайды. Олай болса, Теорема5 бойынша ' түзуі ' шеңберімен жанасады. Ғ' фигурасын салу оңай, себебі В', ' – берілген фигуралардың образдары, ал ' - В' нүктесі арқылы өтетін және ' шеңберімен жанасатын түзу. Онда f инверсиясында ' түзуінің образы болатын шеңберін Теорема3 бойынша салу оңай.
С
алу: 1) Центрі А нүктесі болатын және
шеңберімен қиылысатын кез – келген
шеңбері (81-сурет)
2) ОА түзуінің шеңберімен қиылысу