Файл: Методические рекомендации по организации и проведению лабораторных работ и практических занятий специальность 21. 02. 01 Разработка и эксплуатация нефтяных и газовых месторождений.docx

Таблица №2

Номер измерения	d мм	h мм	 d мм	 h мм
1
2
3
Средние величины

Высоту цилиндра h измеряют при помощи штангельциркуля один раз. Абсолютную ошибку взять равной половине точности штангельциркуля = 0,05 мм.

Вычислить объем цилиндра:

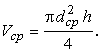(5)

Взвешиванием на весах определяют массу цилиндра m с точностью до = 0,1 г.

Вычисляют плотность вещества цилиндра: . Относительная ошибка при определении плотности цилиндра равна:

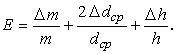(6)

Абсолютная ошибка равна: (7)

Окончательный результат определения плотности вещества цилиндра записывают в виде:



Вопросы для самоконтроля

1. 
   Какие измерения называют прямыми, а какие – косвенными?
   
2. 
   Чем отличаются методики расчёта ошибок для прямых и косвенных измерений?
   
3. 
   В чём состоит принцип равной точности измерений и выполнен ли он в упражнениях 1 и 2 ?
   
4. 
   Составьте формулу для расчёта относительной ошибки по предложенной преподавателем расчётной формуле некоторой косвенно определяемой физической величины.
   
5. 
   Справедливо ли утверждение “Точность прямых измерений пропорциональна числу измерений”? Ответ обоснуйте.
   
6. 
   Сформулируйте правило определения числа прямых измерений. Примените это правило к результатам ваших измерений.
   
7. 
   Какая величина является асимптотой для средней абсолютной ошибки при увеличении числа измерений?
   
8. 
   Чем определяется число значащих цифр при записи результатов расчётов среднего значения физ. величины и его средней абсолютной ошибки?
   
9. 
   С какой точностью надо взять число  при расчёте объёма цилиндра?
   
10. 
    Как следует выбирать масштаб значений физических величин, откладываемых на осях графиков?
    
11. 
    Каким образом на графиках отражают точность измерений и расчётов значений физических величин?
    
12. 
    Какой линией, ломаной или плавной кривой, изображают на графиках зависимости значений функциональных физических величин от значений независимых физических величин? Ответ обоснуйте.
    

---

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ

ЛАБОРАТОРНОЙ РАБОТЫ № 2

---

Тема: «Изучение движения тела по окружности под действием сил упругости и тяжести»

Цель работы: определение центростремительного ускорения шарика при его равномерном движении по окружности.

Теоретическая часть работы.

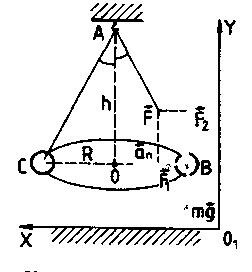
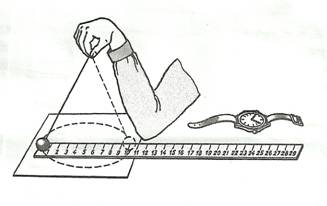
Эксперименты проводятся с коническим маятником. Небольшой шарик движется по окружности радиуса R. При этом нить АВ, к которой прикреплен шарик, описы­вает поверхность прямого кругового конуса. На шарик действуют две силы: сила тяжести и натяжение ни­ти 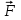(рис. а). Они создают центростремительное ускорение 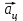, направленное по радиусу к центру окруж­ности. Модуль ускорения можно определить кинематиче­ски. Он равен: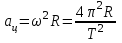



Для определения ускорения надо измерить радиус окружности и период обращения шарика по окружности.

Центростремительное (нормальное) ускорение можно определить также, используя законы динамики.

Согласно второму закону Ньютона 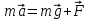. Разло­жим силу 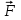на составляющие 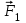и 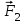, направленные по радиусу к центру окружности и по вертикали вверх.

Т огда второй закон Ньютона запишется следующим об­разом: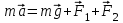



Направление координатных осей выберем так, как показано на рисунке б. В проекциях на ось О₁у уравнение движения ша­рика примет вид: 0 = F₂ — mg. От­сюда F₂ = mg: составляющая 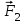уравновешивает силу тяжести 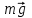, действующую на шарик.

Запишем второй закон Нью­тона в проекциях на ось О₁х:

ma_n = F₁. Отсюда

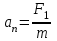
М

---

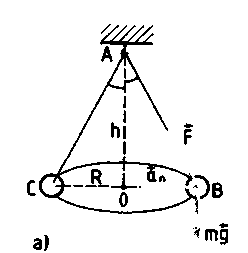
одуль составляющей F₁ мож­но определить различными спосо­бами. Во-первых, это можно сде­лать из подобия треугольников ОАВ и FBF₁:



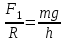
Отсюда 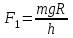и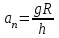

Во-вторых, модуль составляю­щей F₁ можно непосредственно из­мерить динамометром. Для этого оттягиваем горизонтально располо­женным динамометром шарик на расстояние, равное радиусу R окружности (рис. в), и опре­деляем показание динамометра. При этом сила упругости пружи­ны уравновешивает составляющую .

Сопоставим все три выражения для а_n:



, ,

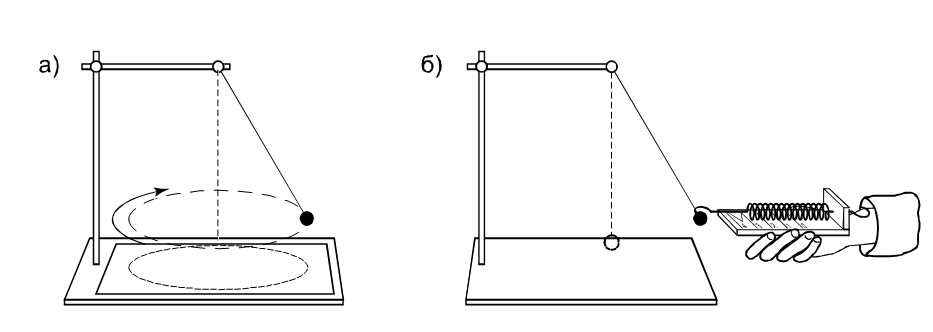
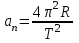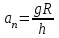и убедимся, что они близки меж­ду собой.

В этой работе с наибольшей тщательностью следует из­мерять время. Для этого полезно отсчитывать возможно большее число оборотов маятника, уменьшая тем самым относительную погрешность.

Взвешивать шарик с точностью, которую могут дать лабораторные весы, нет необходимости. Вполне достаточ­но взвешивать с точностью до 1 г. Высоту конуса и ра­диус окружности достаточно измерить с точностью до 1 см. При такой точности измерений относительные по­грешности величин будут одного порядка.

Оборудование: штатив с муфтой и лапкой, лента измерительная, циркуль, динамометр лабораторный, весы с разновесами, шарик на нити, кусочек пробки с отверстием, лист бумаги, линейка.

Указания к работе.

1. Определяем массу шарика на весах с точностью до 1 г.

2. Нить продеваем сквозь отверстие и зажимаем пробку в лапке штатива (рис. в).

3. Вычерчиваем на листе бумаги окружность, радиус которой около 20 см. Измеряем радиус с точностью до 1 см.

4. Штатив с маятником располагаем так, чтобы продолжение шнура проходило через центр окружности.

5. Взяв нить пальцами у точки подвеса, вращаем маятник так, чтобы шарик описывал окружность, равную начерченной на бумаге.

---

6. Отсчитываем время, за которое маятник совершает, к примеру, N = 50 оборотов.

7. Определяем высоту конического маятника. Для этого измеряем расстояние по вертикали от центра шарик; до точки подвеса.

8. Находим модуль центростремительного ускорение по формулам:

и

9. Оттягиваем горизонтально расположенным динамо метром шарик на расстояние, равное радиусу окружности, и измеряем модуль составляющей . Затем вычисляем ускорение по формуле .

10. Результаты измерений заносим в таблицу.

Номер опыта	R	N	Δt	T= Δt/N	h	m

Сравнивая полученные три значения модуля центростремительного ускорения, сделать вывод:

ЛАБОРАТОРНАЯ РАБОТА №3

Определение коэффициента трения скольжения.
Цель работы:

измерить коэффициент трения скольжения дерева по дереву.

Оборудование:

деревянный брусок, деревянная линейка, набор грузов известной массы (по 100

г), динамометр.

Описание работы.

Если тянуть брусок с грузом по горизонтальной поверхности так, чтобы брусок двигался равномерно, прикладываемая к бруску горизонтальная сила равна по модулю силе трения скольжения F_mр, действующей на брусок со стороны поверхности. Модуль силы трения F_mр связан с модулем силы нормального давления N соотношением F_mр =μ N. Измерив F_mр и N, можно найти коэффициент трения μ по формуле

---