Файл: Отчет по лабораторнопрактической работе 1 исследование электростатического поля методом моделирования в проводящей среде.doc
Добавлен: 10.01.2024
Просмотров: 69
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
и получают точку 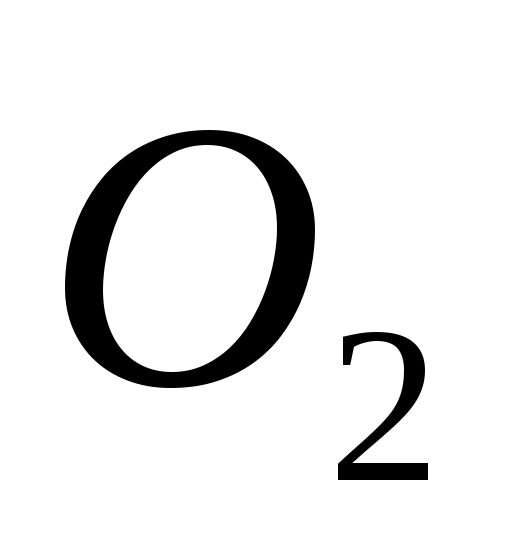 и т.д. Последней точкой на контуре электрода будет та, от которой откладывается отрезок, накрывающий точку O', диаметрально противоположную точке О. Аналогичное построение проводят от точки О в другую сторону. Разделив указанным образом ближайшую к электроду эквипотенциаль, через полученные точки
и т.д. Последней точкой на контуре электрода будет та, от которой откладывается отрезок, накрывающий точку O', диаметрально противоположную точке О. Аналогичное построение проводят от точки О в другую сторону. Разделив указанным образом ближайшую к электроду эквипотенциаль, через полученные точки 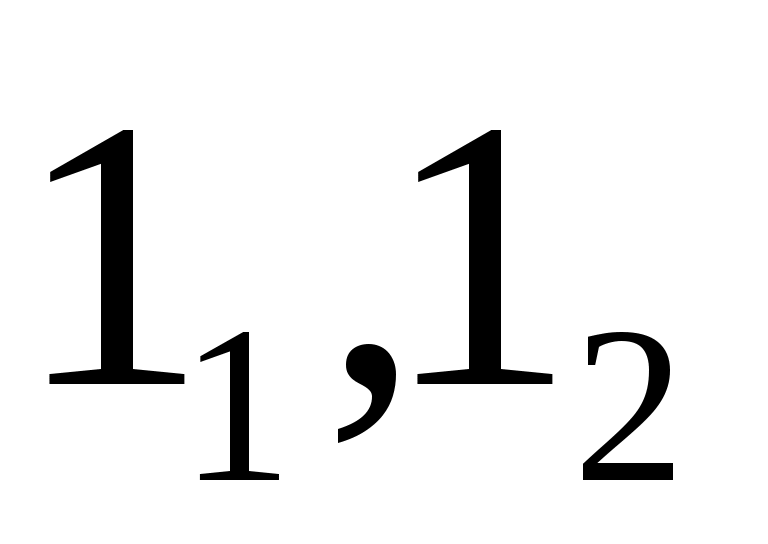 ,… проводят перпендикулярные к ней отрезки до пересечения со следующей эквипотенциалью. Когда будут разделены все эквипотенциали карты поля, полученные точки следует соединить плавными линиями, соблюдая их ортогональность эквипотенциальным линиям в точках пересечения.
,… проводят перпендикулярные к ней отрезки до пересечения со следующей эквипотенциалью. Когда будут разделены все эквипотенциали карты поля, полученные точки следует соединить плавными линиями, соблюдая их ортогональность эквипотенциальным линиям в точках пересечения.
Для вычисления емкости, приходящейся на единицу длины рассматриваемых электродов, необходимо с помощью формулы (1.2) рассчитать поток вектора напряженности через поверхность, охватывающую единицу длины электрода. Для этого следует представить, что ближайшая к электроду замкнутая эквипотенциаль является цилиндром, образующая которого перпендикулярна плоскости листа. Полагая напряженность поля в пределах каждого из отрезков примерно одинаковой, можно вычислить поток
примерно одинаковой, можно вычислить поток 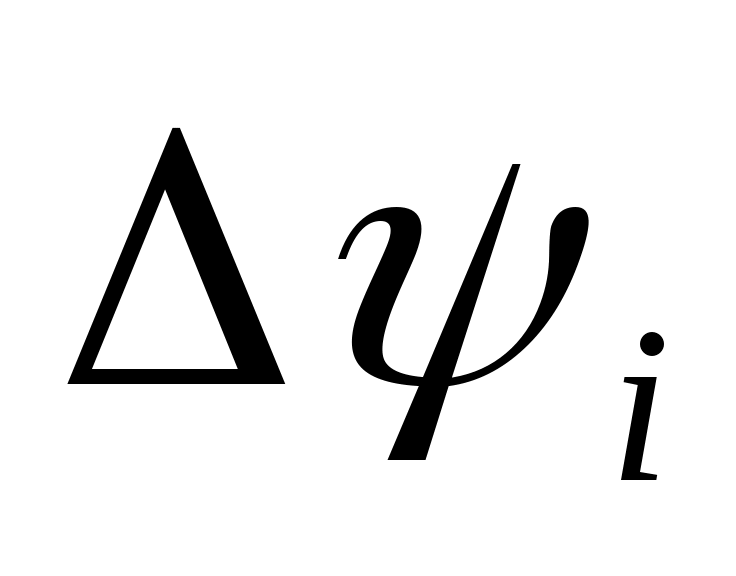 вектора
вектора 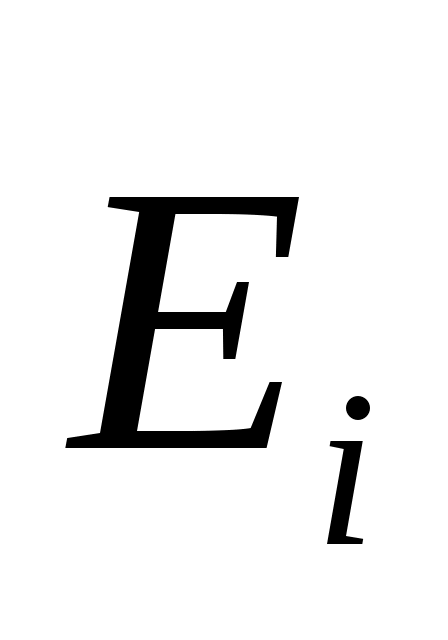 через
через  - й элемент поверхности цилиндра:
- й элемент поверхности цилиндра:
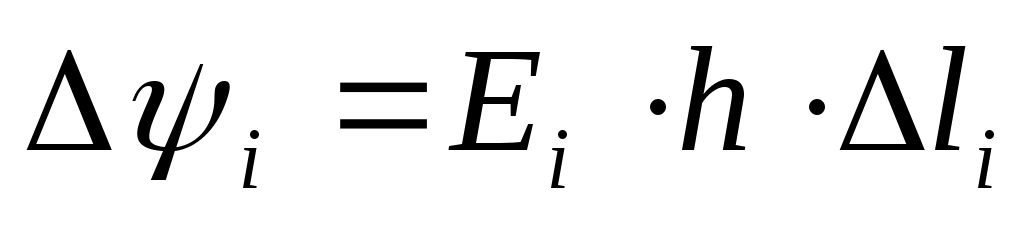 ,
,
где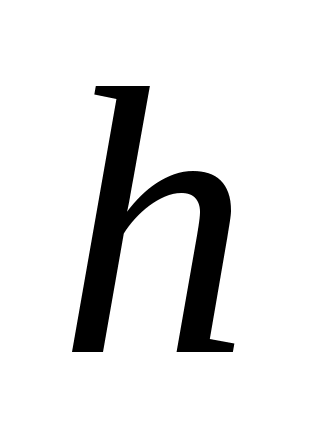 - высота цилиндра,
- высота цилиндра,  - длина отрезка эквипотенциали, измеряемая по карте поля
- длина отрезка эквипотенциали, измеряемая по карте поля 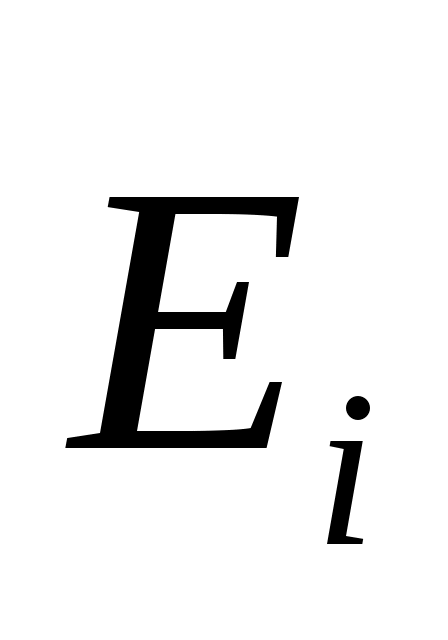 определяется по формуле
определяется по формуле
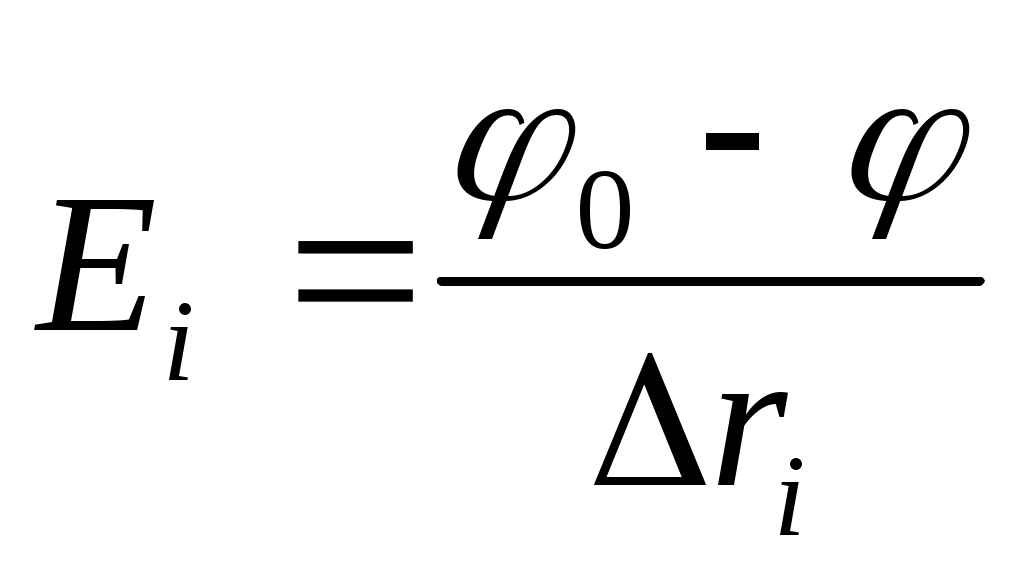 , (1.6)
, (1.6)
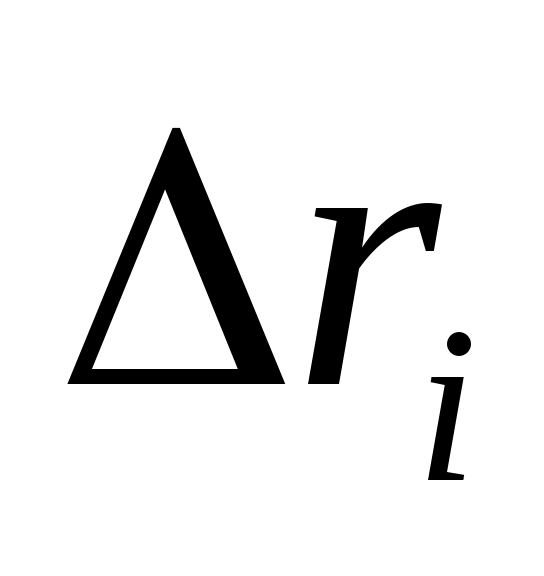 - расстояние между соответствующими отрезками электрода и ближайшей к нему эквипотенциалью; (
- расстояние между соответствующими отрезками электрода и ближайшей к нему эквипотенциалью; (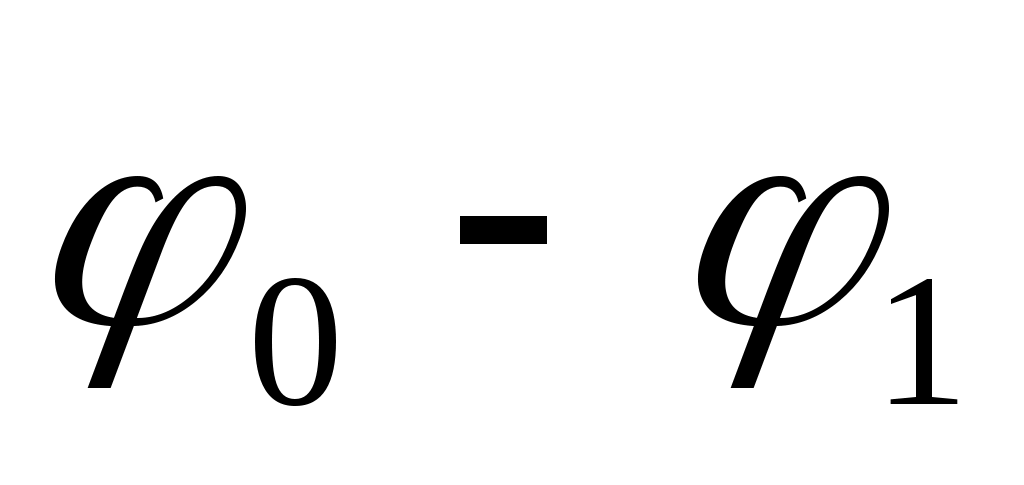 ) - разность потенциалов между электродом и ближайшей к нему эквипотенциалью. Заряд, заключенный внутри замкнутой поверхности цилиндра, вычисляется по теореме Гаусса суммированием потоков
) - разность потенциалов между электродом и ближайшей к нему эквипотенциалью. Заряд, заключенный внутри замкнутой поверхности цилиндра, вычисляется по теореме Гаусса суммированием потоков
 через все элементы поверхности цилиндра:
через все элементы поверхности цилиндра:
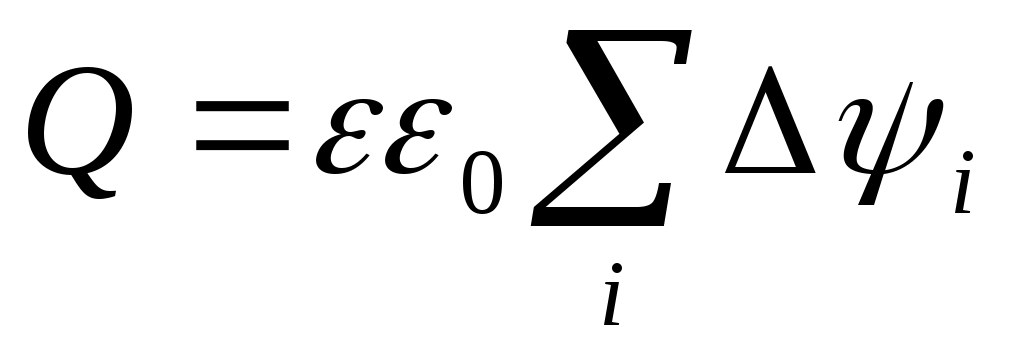 .
.
Последнее соотношение используется для нахождения емкости единицы длины (погонной емкости) моделируемой системы:
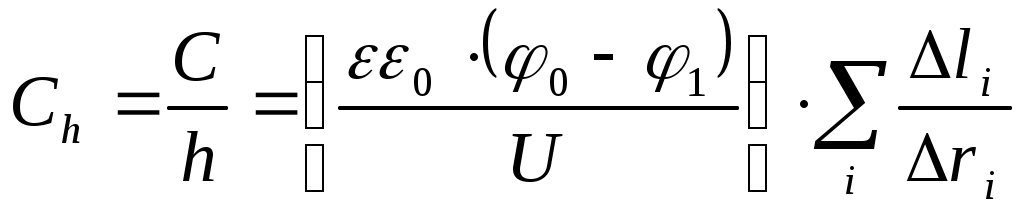 . (1.7)
. (1.7)
№2 Запишите, сформулируйте и объясните закон Кулона. Единица измерения заряда в СИ.
Закон Кулона утверждает, что сила взаимодействия между двумя точечными зарядами пропорциональна произведению их зарядов и обратно пропорциональна квадрату расстояния между ними. Формула закона Кулона выглядит следующим образом:
F = k * (q1 * q2) / r^2
где F - сила взаимодействия, q1 и q2 - заряды двух точечных зарядов, r - расстояние между ними, k - постоянная Кулона, которая зависит от единиц измерения.
Единица измерения заряда в СИ - это кулон. Она определяется как количество электричества, прошедшее через проводник за одну секунду при силе тока в один ампер.
№32 Чему равна сила, действующая на точечный заряд, помещенный в центр равномерно заряженной сферы?
Если поместить точечный заряд в центр равномерно заряженной сферы, то на него не будет действовать никакая сила, так как электрическое поле в этой точке равно нулю.
Сила, действующая на точечный заряд, помещенный в центр равномерно заряженной сферы, равна нулю.
Для вычисления емкости, приходящейся на единицу длины рассматриваемых электродов, необходимо с помощью формулы (1.2) рассчитать поток вектора напряженности через поверхность, охватывающую единицу длины электрода. Для этого следует представить, что ближайшая к электроду замкнутая эквипотенциаль является цилиндром, образующая которого перпендикулярна плоскости листа. Полагая напряженность поля в пределах каждого из отрезков
где
Последнее соотношение используется для нахождения емкости единицы длины (погонной емкости) моделируемой системы:
№2 Запишите, сформулируйте и объясните закон Кулона. Единица измерения заряда в СИ.
Закон Кулона утверждает, что сила взаимодействия между двумя точечными зарядами пропорциональна произведению их зарядов и обратно пропорциональна квадрату расстояния между ними. Формула закона Кулона выглядит следующим образом:
F = k * (q1 * q2) / r^2
где F - сила взаимодействия, q1 и q2 - заряды двух точечных зарядов, r - расстояние между ними, k - постоянная Кулона, которая зависит от единиц измерения.
Единица измерения заряда в СИ - это кулон. Она определяется как количество электричества, прошедшее через проводник за одну секунду при силе тока в один ампер.
№32 Чему равна сила, действующая на точечный заряд, помещенный в центр равномерно заряженной сферы?
Если поместить точечный заряд в центр равномерно заряженной сферы, то на него не будет действовать никакая сила, так как электрическое поле в этой точке равно нулю.
Сила, действующая на точечный заряд, помещенный в центр равномерно заряженной сферы, равна нулю.