Файл: Измерение радиуса кривизны линзы методом интерференционных колец ньютона.docx
Добавлен: 10.01.2024
Просмотров: 269
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Радиусы колец, измеренные в разных направлениях, будут иметь разные значения. На рис. 5 отмечены радиусы первого светлого кольца во взаимно перпендикулярных направлениях. Величину радиуса кольца произвольного m - порядка мы определим, как среднее арифметическое радиусов, измеренных во взаимно перпендикулярных направлениях

2
???????? = 〈????〉 = ????????????+???????????? . (16)
Величины ???????????? и ???????????? находим с помощью измерительной шкалы, вставленной в окуляр микроскопа. Если цена деления шкалы равна С, а значениям ???????????? и ???????????? соответствуют ???????????? и ???????????? чисел делений шкалы, величину ???????? можно вычислить по формуле (17), переписав её в виде:


2
???????? = ???? ∙ (???????????? + ???????????? ). (17)
-
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
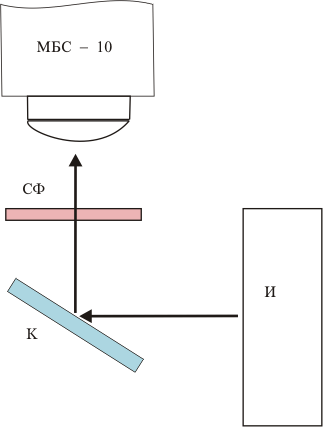
 Установка состоит из измерительного микроскопа МБС – 10 (рис.6), кассеты с линзой и пластинкой «К», светофильтра «СФ», источника света «И». Для определения цены деления измерительной шкалы окуляра служит линейка, закреплённая на одном основании с кассетой «К».
Установка состоит из измерительного микроскопа МБС – 10 (рис.6), кассеты с линзой и пластинкой «К», светофильтра «СФ», источника света «И». Для определения цены деления измерительной шкалы окуляра служит линейка, закреплённая на одном основании с кассетой «К».Рисунок 6 - Лабораторная установка
-
ЗАДАНИЕ

 Основные формулы для расчета:
Основные формулы для расчета:| № форму лы | Формула | Величины, входящие в формулы |
| 19 | 10−3 ???? = ???? | С – цена одного деления шкалы микроскопа, Z –число интервалов измерительной шкалы микроскопа между серединами двух соседних миллиметровых меток линейки |
| 18 | ???? = ???? ∙ (???? + ???? ) ???? 2 ???????? ???????? | ???????? – величина радиуса кольца m- порядка С–цена одного деления шкалы ???????????? – число делений шкалы микроскопа, соответствующих радиусу кольца порядка mв горизонтальном направлении ???????????? –число делений шкалы микроскопа, соответствующих радиусу кольца порядка mв вертикальном направлении |
| 16 | ????2 − ????2 ???? = ???????? ????(???? − ????) | ???? – длина волны используемого света, mи ???? –порядки (номера) светлых колец ???????? –величина радиуса кольца m- порядка |
-
Определение цены деления измерительной шкалы окуляра микроскопа.-
Из поля зрения микроскопа выведен светофильтр, введена в поле зрения линейка с миллиметровыми делениями. Получено резкое изображение штрихов линейки на фоне измерительной шкалы микроскопа (рис.6). -
Если между серединами двух соседних миллиметровых меток линейки укладывается Z интервалов измерительной шкалы, то цена деления измерительной шкалы определяется по формуле:
-
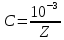 [
[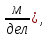 (19)
(19)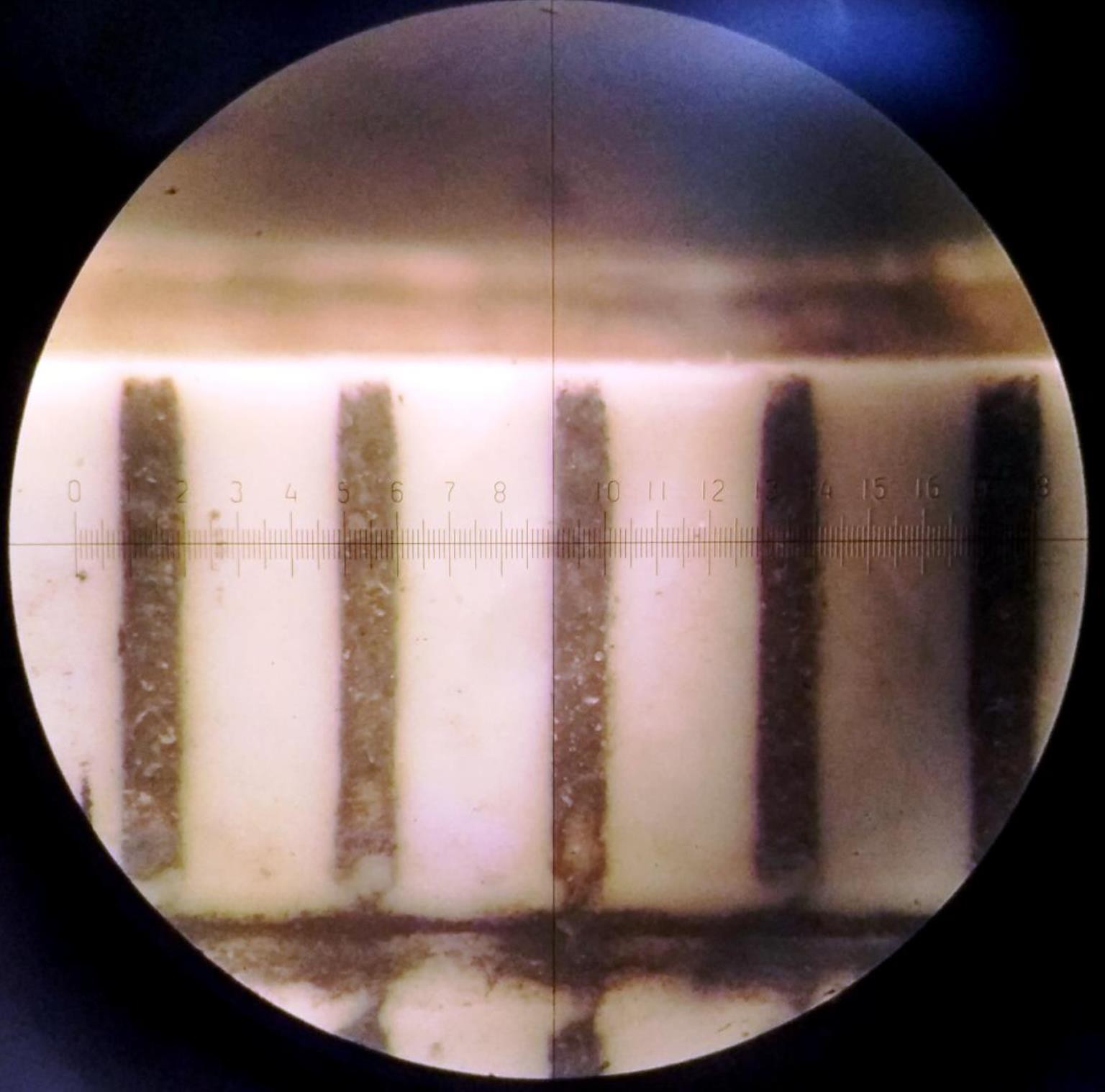
Рисунок 8 - Определение цены деления шкалы микроскопа
-
По рис.8 определяем Z.
Z=41 дел.
-
По формуле (18) определяем цену деления шкалы микроскопа.
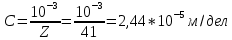
-
Исследование интерференционного спектра.-
Убираем из поля зрения линейку. Вводим в поле зрения кассету с линзой и пластиной и наблюдаем кольца Ньютона без светофильтра (Рис.9).
-

Рисунок 9 - Вид интерференционной картины без светофильтра
-
Определение радиуса кривизны линзы.- Определяем значения порядков светлых колец ℓ=1 и m=4, согласно номеру своего варианта (№ 1).
-
В поле зрения введен светофильтр («СФ» на рис.4). Длина волны, которую пропускает светофильтр, = 640 нм. Интерференционная картина, наблюдаемая со светофильтром, показана на рис. 8 и 9. Красные (светлые) кольца – максимумы интенсивности, темные кольца – минимумы интенсивности
-

Порядок кольца
NmX
NmY
Радиус кольца rm,,м
Радиус кривизны
линзы R, м
ℓ=1
33
27
0,0007
0,495 м
m=4
55
45
0,0012
Подготавливаем таблицу измерений.
Таблица 2
-
Определяем количество делений, соответствующих радиусу кольца заданного порядка ℓ по горизонтали NmXи по вертикали NmY.(рис.10 и рис.11).Результаты заносим в таблицу 2. -
 Повторяем операцию п. 4.3.3 для m-того светлого кольца, записать значения ???????????? и ???????????? для этого максимума.
Повторяем операцию п. 4.3.3 для m-того светлого кольца, записать значения ???????????? и ???????????? для этого максимума.

14
Рисунок 10 - Горизонтальное расположение шкалы микроскопа

Рисунок 11 - Вертикальное расположение шкалы микроскопа
-
Вычисляем радиусы максимумов первого и четвертого порядков по формуле (18).
rl =
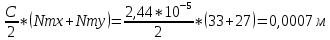
rm =
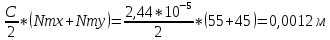
-
Вычисляем радиус кривизны линзы Rрас. по формуле (16). Значение длины электромагнитной волны = 640 нм:
R =
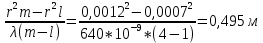
-
Рассчитываем относительную погрешность радиуса кривизны линзы по формулам:
σ =
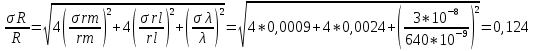
где:
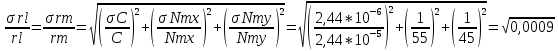
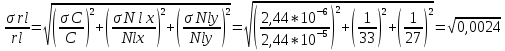
При расчётах принимаем: ???? = 3 ∙ 10−8 м С = 0,1 С,
NmX
NmY
1.
-
Рассчитываем абсолютную погрешность радиуса кривизны линзы по формуле:
∆???? = ????рас. ∙ ????
∆???? =0,495*0,124=0,061 м
-
Запишем конечный результат для радиуса кривизны линзы в виде:
???? = ????рас. ± ∆???? .
R = 0,495±0,061 м
-
Делаем основные выводы по выполненной работе:
- закрепили знания по основам теории интерференции;
- освоили применение интерференционного метода для измерения радиуса кривизны плоско-выпуклой линзы;
- познакомились с явлением колец Ньютона.
5 КОНТРОЛЬНЫЕ ВОПРОСЫ
1 Дайте понятие волнового процесса, расскажите о структуре электромагнитной волны.
Ответ: Волновым процессом называется любое изменение (возмущение) состояния сплошной среды, распространяющееся с конечной скоростью и несущее энергию. Электромагнитная волна имеет сложную пространственную структуру.
Электромагнитная волна представляет собой совокупность двух составляющих (электрическую и магнитную), которые совершают колебания в двух взаимно перпендикулярных плоскостях.
2 Дайте определение интерференции. Какие волны называются когерентными?
Ответ: Интерференция волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга. Сопровождается чередованием максимумов (пучностей) и минимумов (узлов) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности
фаз накладывающихся волн.
Когерентные волны – волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.
3 Объясните условия максимума и минимума интенсивности интерференционной картины. Дайте определение оптической разности хода двух лучей. Запишите формулы для условий максимума и минимума.
Ответ: Если оптическая разность хода D равна целому числу длин волн l 0, т.е. то колебания, возбуждаемые в точке М обеими волнами, будут происходить в одинаковой фазе, и в точке М будет наблюдаться