Файл: Измерение радиуса кривизны линзы методом интерференционных колец ньютона.docx
Добавлен: 10.01.2024
Просмотров: 271
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
иллюстрирует условия максимума и минимума при интерференции. На нем по оси абсцисс отложена оптическая разность хода двух волн, по оси ординат интенсивность результирующей волны
I. Как видно из рисунка, при оптической разности хода (ОРХ) равной нулю наблюдается максимум интенсивности при изменении ОРХ на величину равную длине волны снова возникает максимум, а при изменении ОРХ на пол длины волны попадаем в минимум
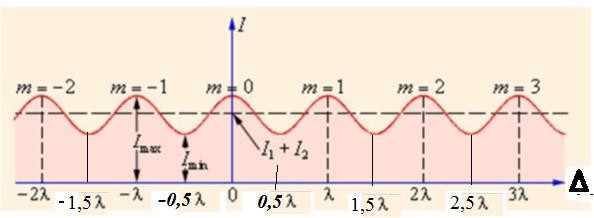
Рисунок 3 - Распределение интенсивности в интерференционной картине в зависимости от величины оптической разности хода. Целое число m – порядок интерференционного максимума
В реальном эксперименте не существует независимых источников когерентных волн, поэтому при наложении света от двух независимых источников интерференции не происходит, интенсивность света во всех точках равна сумме интенсивностей, созданных каждым источником. Это объясняется тем, что свет от обычного источника состоит из цугов волн (кратковременных импульсов), которые независимо излучаются отдельными атомами. Время излучения одного атома имеет порядок величины 108 с. В результате этого в световой волне происходят через краткие промежутки времени случайные изменения начальной фазы колебаний светового вектора, изменяется также случайным образом направление колебаний. Две когерентные световые волны для наблюдения интерференции получают, разделив каким-либо образом одну световую волну. Если две части одной световой волны снова наложить друг на друга, возникает интерференционная картина
Разделение одной волны на две когерентные волны можно проделать различными способами. В частности, разделение на две когерентные волны происходит и при падении света на плоско параллельную пластинку (пленку), отличающуюся по своим оптическим свойствам от окружающей среды. При отражении падающей световой волны от верхней и нижней поверхностей пластинки получаются две когерентные волны. Чтобы в обеих волнах присутствовали излучения одинаковых атомов, пластинка (пленка) должна быть тонкой. Поэтому явление интерференции в этом случае получило название интерференции света в тонких пленках. Если при освещении такой
пластинки монохроматическим светом (светом, содержащим волны одной длины волны, например, красным светом с длиной волны 600 нм), то при выполнении условия максимума пластика в отраженном свете будет красной, а при условии минимума она будет не прозрачной, темной.
Если рассмотреть интерференцию на клине с очень малым углом наклона, то там также, как и в плоско - параллельной пластинке световые лучи отразятся от двух сторон клина, но при движении вдоль клина толщина клина будет меняться и будут поочередно меняться условия максимума и минимума, т.е.
наблюдатель увидит клин полосатым. Такие полосы называются полосами равного наклона, т.к. у клина угол постоянный. Разновидностью полос равного наклона являются кольца Ньютона, но если на клине полосы прямоугольные, то здесь мы имеем дело с кольцами исходя из геометрии задачи.
Кольца Ньютона наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис. 4). Роль клина, от поверхности которого отражаются волны, играет зазор между пластинкой и линзой вблизи точки соприкосновения пластинки и линзы (вследствие большой толщины пластинки и линзы за счет отражений от других поверхностей интерференционные полосы не возникают). При нормальном падении света полосы равной толщины имеют вид окружностей, при наклонном – эллипсов.
Используя метод колец Ньютона, можно определить
радиус кривизны поверхности линзы, обнаружить дефекты полировки ее поверхности (сколы и шероховатости), этот метод является одним из основных при изготовлении и контроле качества линз.
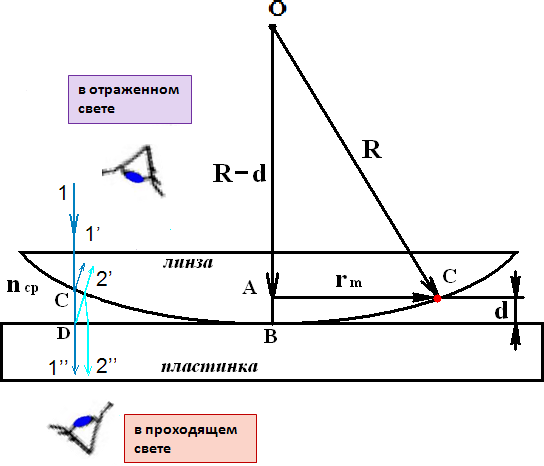
Рисунок 4 - Схема образования интерференционных колец Ньютона Пусть электромагнитная волна «1» (рис. 4), излучаемая источником света,
падает перпендикулярно плоской поверхности на плоско-выпуклую линзу, приведённую в контакт со стеклянной пластиной. В точке «С» происходит разделение волны «1» на две: отраженную от нижней поверхности линзы (волна «1'») и отраженную от верхней поверхности стеклянной пластинки
(волна «2'»). Эти волны будут интерферировать. Для наблюдения интерференционной картины, возникающей на границе раздела «воздушный клин – линза», в работе используется измерительный микроскоп «М». Интерференционная картина, наблюдаемая в микроскоп «М», имеет вид концентрических колец, симметричных относительно точки соприкосновения линзы и пластины. Исторически такая картина получила названия колец Ньютона, первая публикация о которых была им сделана в 1675 году.
Из рис. 4 следует, что оптическая разность хода между волнами «1'» и «2'» равна удвоенной толщине зазора:
∆= |????????| ∙ ???? + |????????| ∙ ???? + ????
2
(7)
где – длина интерферирующих волн, а n – показатель преломления среды, находящейся в зазоре между линзой и пластинкой. Прибавление ???? к оптической
2
длине пути волны «2'» связано с тем, что при её отражении от пластины «П» в
точке «D» (отражение от оптически более плотной среды) фаза волны изменяется на π.
Из формулы (7) следует, что
∆= 2???? ∙ ???? + ???? . (8)
2
В случае, если в точке С выполняется условие максимума интенсивности (5), то формулу (8) можно переписать в виде:
2???? ∙ ???? + ???? = ???????? , (9)
2
где m = 0, 1, 2, … - порядок максимума.
Взаимосвязь толщины воздушного клина d с радиусом кривизны линзы Rнайдём из треугольника АОС. ОВ=ОС=R радиусу кривизны линзы. Толщина зазора d = АВ = ОВ – ОА. Длина катета ОА = R d. По теореме Пифагора:
????
????2 = (???? − ????)2 + ????2 , (10)
где rm– радиус концентрического кольца, соответствующего mпорядку интерференционного максимума.
Раскроем скобки в выражении (10).
????
????2 = ????2 − 2???????? + ????2 + ????2 (11)
В условиях данного эксперимента радиус кривизны линзы R по порядку величины соответствует метрам, радиус колец Ньютона rmпримерно соответствует миллиметрам, толщина зазора d, где наблюдаются кольца
????
Ньютона микрометрам. Таким образом, ???????? ≫ ???? и d2можно пренебречь по сравнению с ????2. Формула (11) упрощается:
????
2
???? ≈ ????. (12)
2????
Из (9) и (12) следует, что для двух максимумов различных порядков mи ℓ
справедливы следующие выражения:
????
2
???? ∙ ???? + ????
???? 2
= ???????? и
2
????
???? ∙ ???? + ????
???? 2
= ???????? . (13)
А радиус светлого кольца Ньютона порядка mв отраженном свете равен:
(????−1)????????
???? √ 2
???? = . (14)
????
Вычитая почленно уравнения (13) и учитывая, что в данной лабораторной работе между линзой и пластинкой находится воздух (n 1), получаем формулу для расчёта радиуса кривизны линзы:
????2 −????2
???? =???? ????
????(????−????)
(15)
При нормальном падении света на плоскую поверхность линзы совокупность интерференционных максимумов одного порядка должна иметь форму кольца. Однако из-за того, что в нашей установке угол падения не равен нулю (наклонное падение), а также из-за неравномерного прижима линзы к пластине (рис.2), шероховатости поверхностей пластины и линзы, форма максимума несколько отличается от окружности (рис. 3).
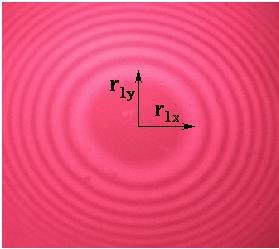
Рисунок 5 - Схема измерения среднего радиуса кольца произвольного
порядка.
I. Как видно из рисунка, при оптической разности хода (ОРХ) равной нулю наблюдается максимум интенсивности при изменении ОРХ на величину равную длине волны снова возникает максимум, а при изменении ОРХ на пол длины волны попадаем в минимум
Рисунок 3 - Распределение интенсивности в интерференционной картине в зависимости от величины оптической разности хода. Целое число m – порядок интерференционного максимума
Способы получения когерентных волн
В реальном эксперименте не существует независимых источников когерентных волн, поэтому при наложении света от двух независимых источников интерференции не происходит, интенсивность света во всех точках равна сумме интенсивностей, созданных каждым источником. Это объясняется тем, что свет от обычного источника состоит из цугов волн (кратковременных импульсов), которые независимо излучаются отдельными атомами. Время излучения одного атома имеет порядок величины 108 с. В результате этого в световой волне происходят через краткие промежутки времени случайные изменения начальной фазы колебаний светового вектора, изменяется также случайным образом направление колебаний. Две когерентные световые волны для наблюдения интерференции получают, разделив каким-либо образом одну световую волну. Если две части одной световой волны снова наложить друг на друга, возникает интерференционная картина
Разделение одной волны на две когерентные волны можно проделать различными способами. В частности, разделение на две когерентные волны происходит и при падении света на плоско параллельную пластинку (пленку), отличающуюся по своим оптическим свойствам от окружающей среды. При отражении падающей световой волны от верхней и нижней поверхностей пластинки получаются две когерентные волны. Чтобы в обеих волнах присутствовали излучения одинаковых атомов, пластинка (пленка) должна быть тонкой. Поэтому явление интерференции в этом случае получило название интерференции света в тонких пленках. Если при освещении такой
пластинки монохроматическим светом (светом, содержащим волны одной длины волны, например, красным светом с длиной волны 600 нм), то при выполнении условия максимума пластика в отраженном свете будет красной, а при условии минимума она будет не прозрачной, темной.
Если рассмотреть интерференцию на клине с очень малым углом наклона, то там также, как и в плоско - параллельной пластинке световые лучи отразятся от двух сторон клина, но при движении вдоль клина толщина клина будет меняться и будут поочередно меняться условия максимума и минимума, т.е.
наблюдатель увидит клин полосатым. Такие полосы называются полосами равного наклона, т.к. у клина угол постоянный. Разновидностью полос равного наклона являются кольца Ньютона, но если на клине полосы прямоугольные, то здесь мы имеем дело с кольцами исходя из геометрии задачи.
Кольца Ньютона наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис. 4). Роль клина, от поверхности которого отражаются волны, играет зазор между пластинкой и линзой вблизи точки соприкосновения пластинки и линзы (вследствие большой толщины пластинки и линзы за счет отражений от других поверхностей интерференционные полосы не возникают). При нормальном падении света полосы равной толщины имеют вид окружностей, при наклонном – эллипсов.
Используя метод колец Ньютона, можно определить
радиус кривизны поверхности линзы, обнаружить дефекты полировки ее поверхности (сколы и шероховатости), этот метод является одним из основных при изготовлении и контроле качества линз.
Рисунок 4 - Схема образования интерференционных колец Ньютона Пусть электромагнитная волна «1» (рис. 4), излучаемая источником света,
падает перпендикулярно плоской поверхности на плоско-выпуклую линзу, приведённую в контакт со стеклянной пластиной. В точке «С» происходит разделение волны «1» на две: отраженную от нижней поверхности линзы (волна «1'») и отраженную от верхней поверхности стеклянной пластинки
(волна «2'»). Эти волны будут интерферировать. Для наблюдения интерференционной картины, возникающей на границе раздела «воздушный клин – линза», в работе используется измерительный микроскоп «М». Интерференционная картина, наблюдаемая в микроскоп «М», имеет вид концентрических колец, симметричных относительно точки соприкосновения линзы и пластины. Исторически такая картина получила названия колец Ньютона, первая публикация о которых была им сделана в 1675 году.
Из рис. 4 следует, что оптическая разность хода между волнами «1'» и «2'» равна удвоенной толщине зазора:
∆= |????????| ∙ ???? + |????????| ∙ ???? + ????2
(7)
где – длина интерферирующих волн, а n – показатель преломления среды, находящейся в зазоре между линзой и пластинкой. Прибавление ???? к оптической2
длине пути волны «2'» связано с тем, что при её отражении от пластины «П» в
точке «D» (отражение от оптически более плотной среды) фаза волны изменяется на π.
Из формулы (7) следует, что
∆= 2???? ∙ ???? + ???? . (8)2
В случае, если в точке С выполняется условие максимума интенсивности (5), то формулу (8) можно переписать в виде:
2???? ∙ ???? + ???? = ???????? , (9)2
где m = 0, 1, 2, … - порядок максимума.
Взаимосвязь толщины воздушного клина d с радиусом кривизны линзы Rнайдём из треугольника АОС. ОВ=ОС=R радиусу кривизны линзы. Толщина зазора d = АВ = ОВ – ОА. Длина катета ОА = R d. По теореме Пифагора:
????
????2 = (???? − ????)2 + ????2 , (10)
где rm– радиус концентрического кольца, соответствующего mпорядку интерференционного максимума.
Раскроем скобки в выражении (10).
????
????2 = ????2 − 2???????? + ????2 + ????2 (11)
В условиях данного эксперимента радиус кривизны линзы R по порядку величины соответствует метрам, радиус колец Ньютона rmпримерно соответствует миллиметрам, толщина зазора d, где наблюдаются кольца
????
Ньютона микрометрам. Таким образом, ???????? ≫ ???? и d2можно пренебречь по сравнению с ????2. Формула (11) упрощается:
????
2
???? ≈ ????. (12)
2????
Из (9) и (12) следует, что для двух максимумов различных порядков mи ℓ
справедливы следующие выражения:
????
2
???? ∙ ???? + ????
???? 2
= ???????? и
2
????
???? ∙ ???? + ????
???? 2
= ???????? . (13)
А радиус светлого кольца Ньютона порядка mв отраженном свете равен:
(????−1)????????
???? √ 2
???? = . (14)
????
Вычитая почленно уравнения (13) и учитывая, что в данной лабораторной работе между линзой и пластинкой находится воздух (n 1), получаем формулу для расчёта радиуса кривизны линзы:
????2 −????2
???? =???? ????
????(????−????)
(15)
При нормальном падении света на плоскую поверхность линзы совокупность интерференционных максимумов одного порядка должна иметь форму кольца. Однако из-за того, что в нашей установке угол падения не равен нулю (наклонное падение), а также из-за неравномерного прижима линзы к пластине (рис.2), шероховатости поверхностей пластины и линзы, форма максимума несколько отличается от окружности (рис. 3).
Рисунок 5 - Схема измерения среднего радиуса кольца произвольного
порядка.