Файл: Измерение радиуса кривизны линзы методом интерференционных колец ньютона.docx

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации
СибГУТИ

Кафедра физики

Лабораторная работа №7.2

«ИЗМЕРЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ МЕТОДОМ ИНТЕРФЕРЕНЦИОННЫХ КОЛЕЦ НЬЮТОНА»

Выполнил: студент гр. ЗМ-221

Колчева В.С.

№ Зачетной книжки: 123220061

Преподаватель: Черевко А.Г.

Измерения сняты
	дата			подпись
Отчет принят
Защита:
оценка	дата			подпись

Новосибирск 2023 г.

1. 
   ЦЕЛЬ РАБОТЫ
   

Закрепить знания по основам теории интерференции. Освоить применение интерференционного метода для измерения радиуса кривизны плоско- выпуклой линзы.

2. 
   ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
   

Видимый свет представляет собой электромагнитную волну с частотой (????) в диапазоне Гц и длиной волны (λ) в вакууме: (380 − 780) нм; (0,38 − 0,78) ∙ 10⁻⁶м. Такие электромагнитные волны называются световыми волнами

	Цвет	Диапазон длин волн, нм		Рисунок 1 - Диапазоны длин волн видимого света. Электромагнитные излучение с длиной волны, λ менее 380 нм относятся к ультрафиолетовому излучению. а с λ> 760 нм к инфракрасному излучению и человеческим глазом не фиксируется
	Фиолето вый	380-450
	Синий	450-480
	Голубой	480—500
	Зелёный	500—560
	Жёлтый	560—590
	Оранжев ый	590—620
	Красный	620—760

---

В световой волне происходят колебания векторов напряженности электрического и магнитного полей. Эти вектора перпендикулярны друг другу, и оба они перпендикулярны направлению распространения света (Рис. 2).



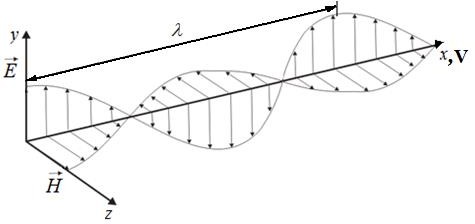
Рисунок 2 - Строение плоской электромагнитной волны.

Для плоской электромагнитной синусоидальной волны (Рис. 2) колебания векторов напряженности электрического и магнитного поля описывается функциями:
E_y  E_mcos_t kx _{0 }

---

1.   1   2   3   4

---

Два условия возникновения интерференции волн:

1- Когерентность волн, такое наложение двух волн, при котором в различных точках пространства колебания световых векторов волн происходит синхронно и возникают устойчивые во времени максимумы и минимумы интенсивности. Это означает – разность фаз двух волн постоянна во времени:

∆???? = ????_???? − ????_???? = ???????????????????? – условие когерентности базовое

Следствие: учитывая, что фаза равна ???? = ⁽???????? − ???????? + ????₀⁾, ???? ???? = 2????/???? получаем, что волны когерентны, если у них одинаковы частоты и разность начальных фаз постоянна:

????_???? = ????_????; ⁽????_???????? − ????_????????⁾ = ???????????????????? – условие когерентности удобное для анализа

2 - Идентичная поляризация двух волн, это означает, что колебания светового вектора происходят в одном направлении, или в близких направлениях.

2. Условия максимума и минимума интенсивности интерференционной картины

   1. 
      Оптическая длина пути, оптическая разность хода волн
      

В вакууме скорость света (с) всегда постоянна и равна с = 3 ∙ 10⁸, м/с. В среде скорость света (V) меньше, чем в вакууме, Отношение этих скоростей называется показателем преломления среды

???? = ????/???? , (2)

Например, в стекле (n=1,5) скорость света в полтора раза меньше, чем в вакууме. Таким образом, для преодоления одного и того-же расстояния свету в стекле понадобится в n раз больше времени, т.е. в 1,5 раза больше времени. Чем в вакууме. Чтобы упростить расчеты при анализе интерференционных и дифракционных явлений вводят понятие оптической длины пути:

Оптическая длина пути - это расстояние, которое прошел бы свет в вакууме за то время, которое он затратил на прохождение заданного пути в веществе. Оптическая длина пути в n раз больше расстояния, пройденного светом в веществе с показателем преломления n:

????_ОПТ = ???????? (3)

Например, свет в стекле с показателем преломления n=1,5 прошел ^{расстояние L Определить оптическую длину пути: L}опт^=nL=1,5L.

Оптическая разность хода (∆) – это разность оптических путей двух интерферирующих лучей от точки их раздвоения до экрана или другого объекта, где создается интерференционная картина

∆= ????_ОПТ2 − ????_ОПТ1 (4)

2. Условия максимума и минимума интенсивности интерференционной картины, записанное через оптическую разность хода лучей - (∆).

Пусть происходит интерференция двух когерентных волн с одинаковыми амплитудами световых векторов E_m1= E_m2= E_m. Если электромагнитные волны приходят в точку наблюдения в фазе, то при их наложении световые вектора волн будут направлены в одну сторону и будут складываются и общая (результирующая) амплитуда будет удвоена (E_РЕЗ= E_m1+ E_m2= 2E_m), а интенсивность результирующей волны будет в 4 раза больше интенсивности исходной волны, т.к. интенсивность пропорциональна квадрату амплитуды, I_РЕЗ= 4I 4(E

---

_m)². В этих точках будут наблюдаться максимумы, т.е. наиболее яркие линии интерференционной картины (максимумы на рисунке 3).

Если волны придут в точку наблюдения в противофазе, то световые вектора будут компенсировать друг друга, они будут направлены в разные стороны и результирующий вектор будет равен разности исходных световых векторов (E_РЕЗ= E_m1– E_m2= 0). В точке наблюдения света не будет – минимуму интенсивности.

Учитывая это и переходя от разности фаз к разности оптических путей получаем условие максимума и минимума интенсивности интерференционной картины, записанное через оптическую разность хода лучей - (∆).

∆= ±???? ∙ ????_????, (m= 0, 1, 2, …) – условие максимума (5)


????
???? = ± (???? + ^????) ∙ ???? , (m= 0, 1, 2, …) – условие минимума (6)


Идеальную интерференционную картину от двух световых волн представляет рисунок 3, который

---