Файл: Купности и их обработки. Такие вопросы рассматриваются в мате матической статистике.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 70
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ся), который зависит не только от доверительной вероятности р, но и от объема выборки п. Коэффициент Стьюдента можно найти из табл. 8.
Запишем неравенство (3.16), подставив в него выражение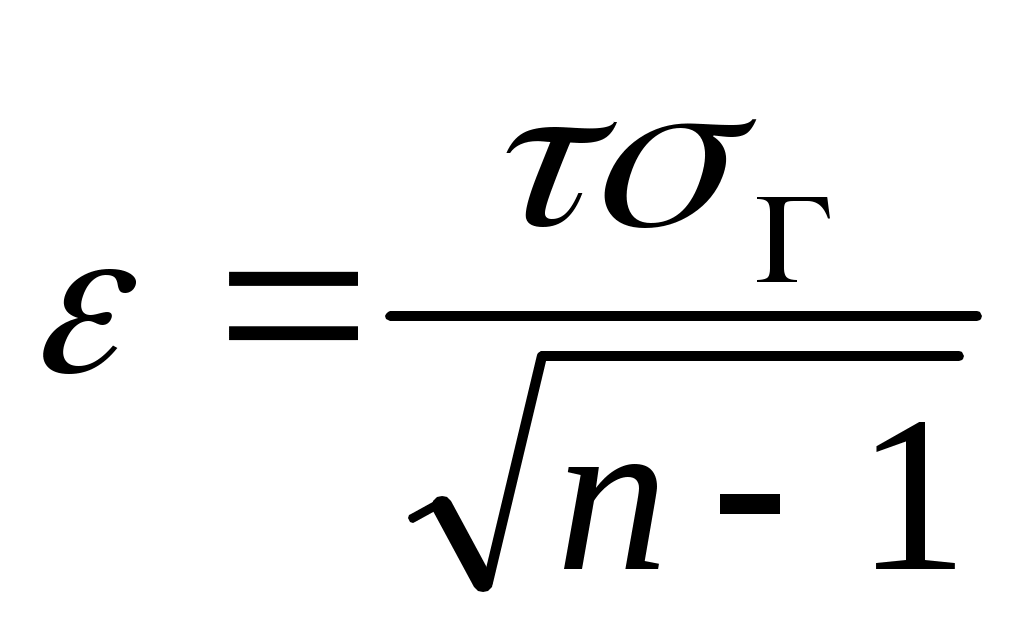 из формулы (3.26):
из формулы (3.26):
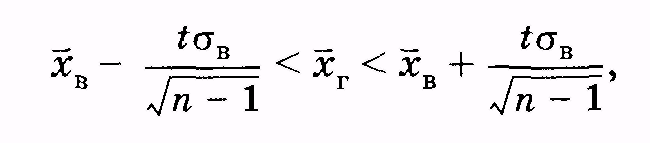 (3.27)
(3.27)
Таблица 8
Отсюда можно вычислить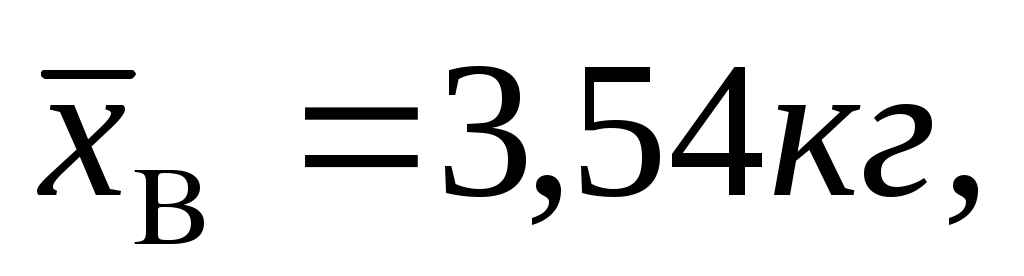 Db = 0,19156 кг2 и в = = 0,43767 кг. Задав доверительную вероятность р = 0,95, находим из табл. 8 для объема выборки п = 10 параметр t= 2,26. Подставляя эти данные в (3.26), получаем для доверительного интервала [см. (3.27)]:
Db = 0,19156 кг2 и в = = 0,43767 кг. Задав доверительную вероятность р = 0,95, находим из табл. 8 для объема выборки п = 10 параметр t= 2,26. Подставляя эти данные в (3.26), получаем для доверительного интервала [см. (3.27)]:
или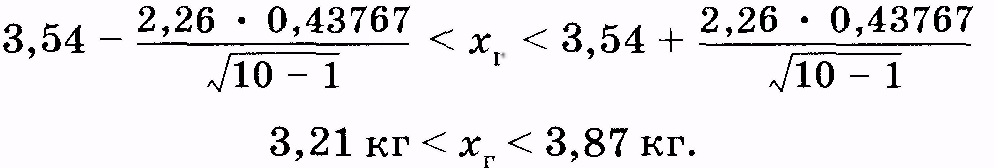 (3.28)
(3.28)
Полезно сопоставить соотношения, полученные для большой (3.25) и малой (3.28) выборок.
Интервальная оценка истинного значения измеряемой величины. Интервальная оценка генеральной средней может быть использована для оценки истинного значения измеряемой величины.
Пусть несколько раз измеряют одну и ту же физическую величину. При этом по разным случайным причинам, вообще говоря, получают разные значения: x1, x2, x3, ... . Будем считать, что нет преобладающего влияния какого-либо фактора на эти измерения.
Истинное значение измеряемой величины (хист) совершенно точно измерить невозможно хотя бы по причине несовершенства измерительных приборов. Однако можно дать интервальную оценку для
этого значения.
Если значения х1, х2, х3, ... рассматривать как варианты выборки, а истинное значение измеряемой величины хист как аналог генеральной средней, то можно по описанным выше правилам найти доверительный интервал, в который с доверительной вероятностью р попадает истинное значение измеряемой величины. Применительно к малому числу измерений (п < 30) из (3.27) получим:
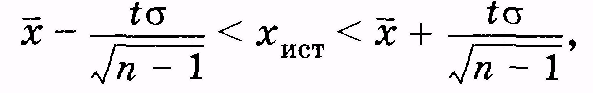 (3.29)
(3.29)
где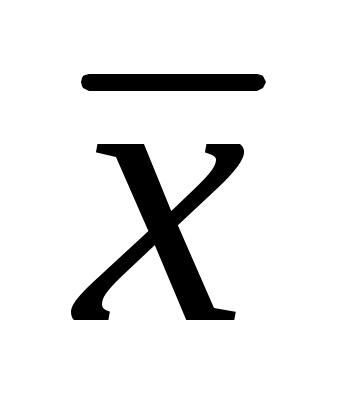 — среднее арифметическое значение из полученных измерений, а — оответствующее им среднее квадратическое отклонение, t—коэффициент Стьюдента.
— среднее арифметическое значение из полученных измерений, а — оответствующее им среднее квадратическое отклонение, t—коэффициент Стьюдента.
Более подробно и разносторонне оценка результатов измерений рассматривается в практикуме (см. [1]).
§3.3. Проверка гипотез
В медико-биологических исследованиях актуальной является задача сравнения выборок, полученных в результате эксперимента, заключающегося в том или ином воздействии на объект. Фактически конечный результат исследования зависит от достоверности различий значений случайной величины в контроле (до воздействия или без него) и опыте (после воздействия). Наиболее просто решается задача определения достоверности различий статистических распределений, если предварительно для выборок рассчитаны доверительные интервалы. Положим, есть два статистических распределения некоторых случайных величин Xи Y. Пусть генеральные средние этих распределений с доверительной вероятностью р = 0,95 находятся в доверительных интервалах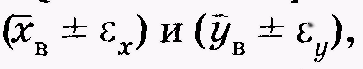 и пусть при этом
и пусть при этом 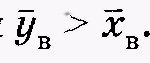 Если соблюдается неравенство
Если соблюдается неравенство 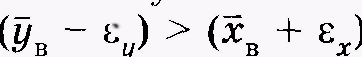 , то не вызывает сомнения, что случайная величина
, то не вызывает сомнения, что случайная величина
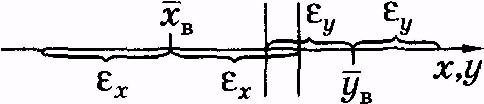
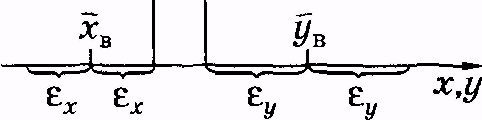
Yсущественно больше случайной величины X(см. рис. 3.3, а). Вероятность этого превышает 0,95.
На рис. 3.3, б представлен вариант, когда выборки частично пересекаются, т. е. когда выполняется неравенство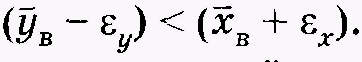 В этом случае целесообразно оценивать достоверность различий выборочных средних
В этом случае целесообразно оценивать достоверность различий выборочных средних  и
и 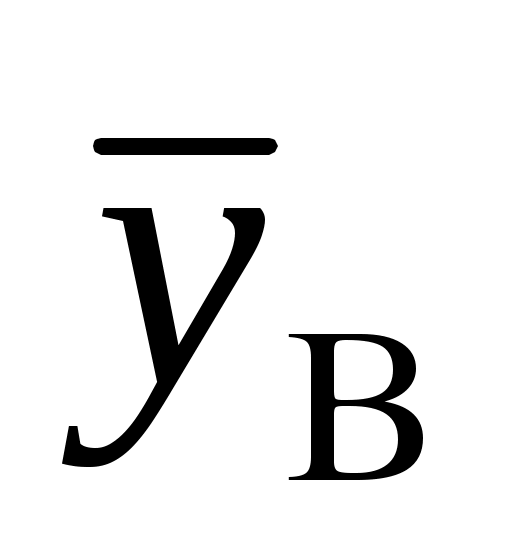 с помощью дополнительных расчетов. Наиболее просто это сделать, предполагая, что случайные величины Xи Yраспределены по нормальному закону. Условием существенности различия двух опытных распределений, являющихся выборками из различных генеральных совокупностей, является выполнение следующего неравенства для опытного и теоретического значений критерия Стьюдента:
с помощью дополнительных расчетов. Наиболее просто это сделать, предполагая, что случайные величины Xи Yраспределены по нормальному закону. Условием существенности различия двух опытных распределений, являющихся выборками из различных генеральных совокупностей, является выполнение следующего неравенства для опытного и теоретического значений критерия Стьюдента: 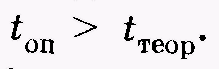 Для нахождения значения toписпользуют следующую формулу:
Для нахождения значения toписпользуют следующую формулу:
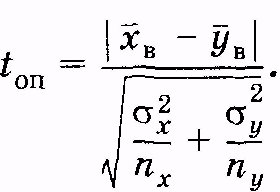
(3.30)
Здесь х и у — выборочные средние квадратические отклонения, пхи пу— число вариант в выборках (объемы выборок), и у — выборочные средние значения.
и у — выборочные средние значения.
а) б)
Рис. 3.3
Теоретическое значение tтeop находят по таблице 10, входными величинами которой являются доверительная вероятность р и параметр f, связанный с числом вариант в выборках. Этот параметр определяют следующим образом. Если х у, то f= пх + п — 2.
Если же х и у различаются на порядок и более, то величина fопределяется по формуле:
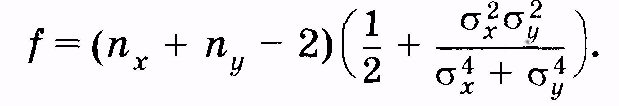 (3.31)
(3.31)
Таблица 10.Значения критерия Стьюдента tтeop при различной доверительной вероятности и значениях параметра f
Запишем неравенство (3.16), подставив в него выражение
Таблица 8
| Объем | Доверительная вероятность, р | |||
| выборки, п | 0,9 | 0,95 | 0,99 | 0,999 |
| 2 | 6,31 | 12,70 | 63,66 | - |
| 3 | 2,92 | 4,30 | 9,93 | 31,60 |
| 10 | 1,83 | 2,26 | 3,25 | 4,78 |
| 15 | 1,76 | 2,15 | 2,95 | 4,07 |
Таблица 9
| Масса, кг | 3,0 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,7 | 3,8 | 4,0 | 4,4 |
| Частота | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Отсюда можно вычислить
или
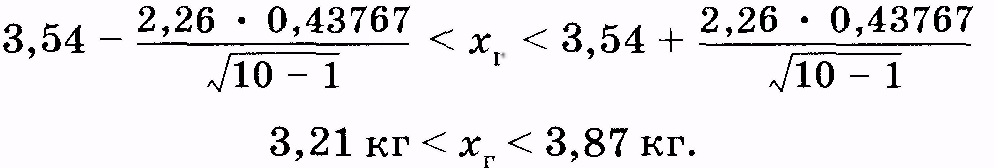 (3.28)
(3.28)Полезно сопоставить соотношения, полученные для большой (3.25) и малой (3.28) выборок.
Интервальная оценка истинного значения измеряемой величины. Интервальная оценка генеральной средней может быть использована для оценки истинного значения измеряемой величины.
Пусть несколько раз измеряют одну и ту же физическую величину. При этом по разным случайным причинам, вообще говоря, получают разные значения: x1, x2, x3, ... . Будем считать, что нет преобладающего влияния какого-либо фактора на эти измерения.
Истинное значение измеряемой величины (хист) совершенно точно измерить невозможно хотя бы по причине несовершенства измерительных приборов. Однако можно дать интервальную оценку для
этого значения.
Если значения х1, х2, х3, ... рассматривать как варианты выборки, а истинное значение измеряемой величины хист как аналог генеральной средней, то можно по описанным выше правилам найти доверительный интервал, в который с доверительной вероятностью р попадает истинное значение измеряемой величины. Применительно к малому числу измерений (п < 30) из (3.27) получим:
где
Более подробно и разносторонне оценка результатов измерений рассматривается в практикуме (см. [1]).
§3.3. Проверка гипотез
В медико-биологических исследованиях актуальной является задача сравнения выборок, полученных в результате эксперимента, заключающегося в том или ином воздействии на объект. Фактически конечный результат исследования зависит от достоверности различий значений случайной величины в контроле (до воздействия или без него) и опыте (после воздействия). Наиболее просто решается задача определения достоверности различий статистических распределений, если предварительно для выборок рассчитаны доверительные интервалы. Положим, есть два статистических распределения некоторых случайных величин Xи Y. Пусть генеральные средние этих распределений с доверительной вероятностью р = 0,95 находятся в доверительных интервалах
Yсущественно больше случайной величины X(см. рис. 3.3, а). Вероятность этого превышает 0,95.
На рис. 3.3, б представлен вариант, когда выборки частично пересекаются, т. е. когда выполняется неравенство
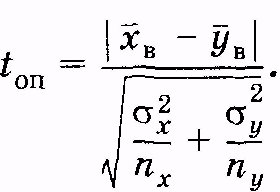
(3.30)
Здесь х и у — выборочные средние квадратические отклонения, пхи пу— число вариант в выборках (объемы выборок),
а) б)
Рис. 3.3
Теоретическое значение tтeop находят по таблице 10, входными величинами которой являются доверительная вероятность р и параметр f, связанный с числом вариант в выборках. Этот параметр определяют следующим образом. Если х у, то f= пх + п — 2.
Если же х и у различаются на порядок и более, то величина fопределяется по формуле:
Таблица 10.Значения критерия Стьюдента tтeop при различной доверительной вероятности и значениях параметра f
| f | Доверительная вероятность, р | f | Доверительная вероятность, р | ||||
| | 0,95 | 0,99 | 0,999 | | 0,95 | 0,99 | 0,999 |
| 1 | 12,71 | 63,60 | | 21 | 2,08 | 2,83 | 3,82 |
| 2 | 4,30 | 9,93 | 31,60 | 22 | 2,07 | 2,82 | 3,79 |
| 3 | 3,18 | 5,84 | 12,94 | 23 | 2,07 | 2,81 | 3,77 |
| 4 | 2,78 | 4,60 | 8,61 | 24 | 2,06 | 2,80 | 3,75 |
| 5 | 2,57 | 4,03 | 6,86 | 25 | 2,06 | 2,79 | 3,73 |
| 6 | 2,45 | 3,71 | 5,96 | 26 | 2,06 | 2,78 | 3,71 |
| 7 | 2,37 | 3,50 | 5,41 | 27 | 2,05 | 2,77 | 3,69 |
| 8 | 2,31 | 3,36 | 5,04 | 28 | 2,05 | 2,76 | 3,67 |
| 9 | 2,26 | 3,25 | 4,78 | 29 | 2,04 | 2,76 | 3,66 |
| 10 | 2,23 | 3,17 | 4,59 | 30 | 2,04 | 2,75 | 3,65 |
| 11 | 2,20 | 3,11 | 4,44 | 40 | 2,02 | 2,70 | 3,55 |
| 12 | 2,18 | 3,06 | 4,32 | 50 | 2,01 | 2,68 | 3,50 |
| 13 | 2,16 | 3,01 | 4,22 | 60 | 2,00 | 2,66 | 3,46 |
| 14 | 2,15 | 2,98 | 4,14 | 80 | 1,99 | 2,64 | 3,42 |
| 15 | 2,13 | 2,95 | 4,07 | 100 | 1,98 | 2,63 | 3,39 |
| 16 | 2,12 | 2,92 | 4,02 | 120 | 1,98 | 2,62 | 3,37 |
| 17 | 2,11 | 2,90 | 3,97 | 200 | 1,97 | 2,60 | 3,34 |
| 18 | 2,10 | 2,88 | 3,92 | 500 | 1,96 | 2,59 | 3,31 |
| 19 | 2,09 | 2,86 | 3,88 | | 1,96 | 2,58 | 3,29 |
| 20 | 2,09 | 2,85 | 3,85 | | | | |