Файл: Купности и их обработки. Такие вопросы рассматриваются в мате матической статистике.doc

щих параметров,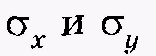 — средние квадратические отклонения. Рассчитанный по формуле (3.32) коэффициент корреляции сравнивают с теоретическим, который находят в специальной таблице с учетом определенного уровня значимости и объема выборки (см. табл. 12). Входными значениями таблицы являются число пар ис­следуемых признаков (п) и уровень значимости (0,05 или 0,01). При этом нулевая гипотеза заключается в том, что корреляцион­ной связи между исследуемыми параметрами не существует. Если получают значения коэффициента корреляции больше таблично­го, с определенной степенью вероятности полагают, что корреля­ция в генеральной совокупности отличается от нуля.

Таблица 12.Критические значения выборочного коэффициента корреляции г для двух уровней значимости

п	0,05	0,01	п	0,05	0,01	п	0,01	0,01	п	0,05	0,01
4	950	990	15	514	641	26	388	496	80	219	288
5	878	959	16	497	623	27	381	487	90	206	272
6	811	917	17	482	66	28	371	478	100	196	258
7	754	874	18	468	590	29	367	470	125	175	230
8	707	834	19	456	575	33	361	463	150	163	210
9	666	798	20	444	561	35	332	435	200	138	182
10	632	765	21	433	549	40	310	407	250	142	163
11	602	735	22	423	537	45	292	384	300	113	148
12	576	708	23	413	523	50	277	364	400	098	128
13	553	684	24	404	515	60	253	333	500	088	115
14	532	661	25	396	505	70	234	308	1000	062	081

---

Примечание. Нуль целых и запятая в значениях rопущены. Ну­левая гипотеза отбрасывается при r > r₀ с данным уровнем значимости (0,05 или 0,01).

Покажем на примере, как рассчитывают коэффициент корре­ляции Бравэ—Пирсона.

*Оценить взаимосвязь частоты пульса Xи максимального артериаль­ного давления Y у детей:

Х (удары/мин) 121,8 119,2 111,3 113,3 98,3 93,8

Y(мм.рт.ст) 99,5 103,0 103,1 106,8 99,1 99,2

Согласно нулевой гипотезе, корреляционной связи между изучае­мыми параметрами нет. Рассчитаем выборочные средние значения и средние квадратичные отклонения для приведенных выше выборок ис­следуемых параметров: = 109,6; 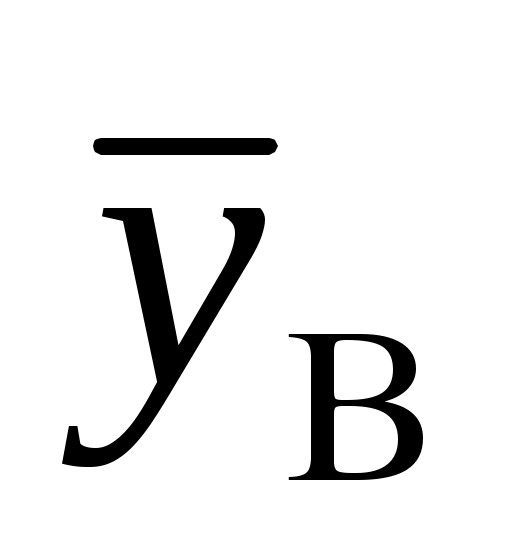= 101,8; _х= 10,29 и _у= 2,81. По формуле (3.32) рассчитываем коэффициент корреляции r= 0,44. Затем обращаемся к таблице 12 и находим для шести пар признаков (п = 6), те­оретическое значение коэффициента корреляции 0,811 при уровне значимости 0,05 и 0,917 при уровне значимости 0,01. В том и другом случае нулевая гипотеза оказывается справедливой и корреляционной связи между анализируемыми признаками не существует с вероятностью 0,95 и 0,99.

Количественное представление зависимости изменений одного признака от изменений другого позволяет получить показатели регрессии. Как правило, анализ регрессии начинают с графиче­ского изображения данных. При большом числе исходных дан­ных для выявления общей закономерности вычисляются средние значения одного признака (у) в группах (классах), соответствую­щих определенному интервалу значений другого признака (х). При построении графика по усредненным данным точки на гра­фике располагаются вдоль так называемой эмпирической линии регрессии. Затем проводят подбор и составление уравнения рег­рессии. С помощью такого уравнения можно теоретически рас­считать значения, которые должен принимать один признак при определенных значениях другого (уравнение прогноза).

Если предполагается существование линейной зависимости между исследуемыми признаками (линейная регрессия), то про­водить регрессионный анализ наиболее просто. Часто при этом применяют графический метод. Для проведения линии регрессии

---

используют прозрачную линейку, придавая ей такое положение, чтобы выше и ниже предполагаемой линии регрессии оказалось приблизительно одинаковое число эмпирических точек. На полу­ченной прямой определяют координаты двух наиболее отдален­ных точек x₁, y_lи х₂, у₂. Затем составляют систему двух уравне­ний:



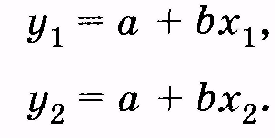
Из полученной системы уравнений определяют неизвестные а и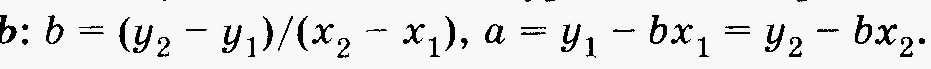 Наконец, при известных коэффициентах а и bзаписывают уравнение прогноза, на основании которого можно рассчитать значение параметра у при известном значении х.

В настоящее время при статистическом анализе эксперимен­тальных данных ироко используются компьютерные вычисли­тельные программы, позволяющие проводить корреляционный и регрессионный анализ. Более подробно практическое применение этого вида анализа рассматривается в курсе социальной гигиены и организации здравоохранения.

---