Файл: Реферат Методика обучения информатике в рамках содержательной линии "Формализация и моделирование" Краснодар.docx
Добавлен: 10.01.2024
Просмотров: 131
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
задачи в тетрадь.
Учитель: что мы делаем на первом этапе построения модели? (изобра- жаем описательную информационную модель: «визуализация траектории движения тела, брошенного под углом к горизонту»).
Учитель вызывает учащегося к интерактивной доске выполнять первый этап построения, изображать модель, остальные выполняют в тетрадях.
С помощью фона «Сетка» и инструмента «умного пера» учащийся изображает условие задачи рис. 3.
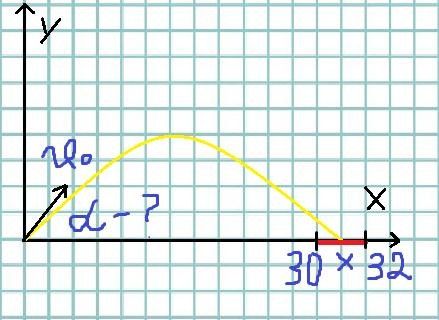 (v0 – начальная скорость, α – угол бросания, х – координата дальности полѐта, y – координата высоты полета, от времени).
(v0 – начальная скорость, α – угол бросания, х – координата дальности полѐта, y – координата высоты полета, от времени).
Рис. 3. Движение тела, брошенного под углом к горизонту Учащийся присаживается на место.
Учитель: сформулируем основные предположения:
 мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;
мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;
 изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g = 9,8 м/с2 и движение по оси OY можно считать равноускоренным;
изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g = 9,8 м/с2 и движение по оси OY можно считать равноускоренным;
 скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси ОX можно считать равно- мерным.
скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси ОX можно считать равно- мерным.
Учитель: теперь нашу информационную модель мы должны предста- вить в формализованную модель в нашем случае математическую. Что для этого мы используем? (формулы равномерного и равноускоренного движе- ния). Записываем все формулы в тетрадь.

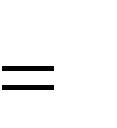 x V0
x V0
cos( ) t
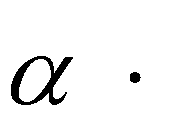

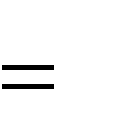 y V0
y V0
sin( ) t
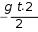
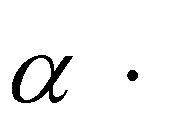 Учитель: где расположена площадка? (на поверхности Земли). Поэтому из второй формулы можно выразить время, которое понадобится мячику, чтобы достичь площадки. (Слайд 5)
Учитель: где расположена площадка? (на поверхности Земли). Поэтому из второй формулы можно выразить время, которое понадобится мячику, чтобы достичь площадки. (Слайд 5)
 t (V0
t (V0
 V
V
sin( )
 sin( )
sin( )
g t ) 0 2
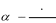
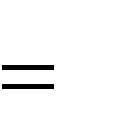
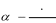
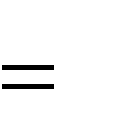 g t 0
g t 0
0 2
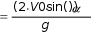 t
t
Учитель: что мы делаем с получившийся формулой? (Подставляем по- лученное выражение для времени в формулу для вычисления координаты x). (Слайд 6)
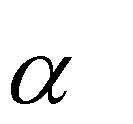
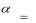

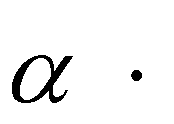



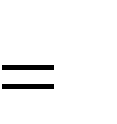 V cos( ) 2 V sin( ) V2 sin(2 )
V cos( ) 2 V sin( ) V2 sin(2 )
x 0 0 0
g g
Учитель: что мы делаем на третьем этапе? (на третьем этапе осуществ- ляем реализацию формализованной модели в компьютерную модель рис. 4. средствами ИКТ, в нашем случае с помощью электронной таблицы).
Учащиеся пересаживаются за компьютеры, открывают заранее подго- товленную учителем компьютерную модель в программе Microsoft Excel под названием «Модель1», рис. 4. Вместе с учителем рассматривают данные в модели.
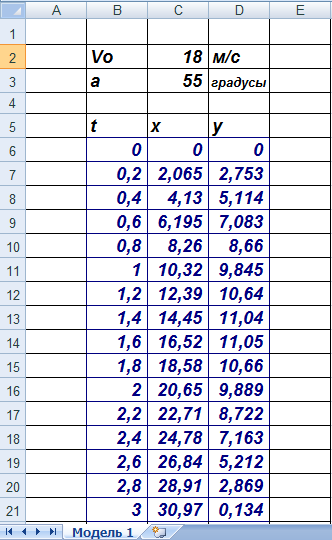
Рис. 4. Компьютерная модель «Движение тела брошенного под углом» в про- грамме Microsoft Excel
Учитель: ребята расскажите, что дано в программе (v0 – начальная ско- рость равна приблизительно 18 м/с, α – угол бросания приблизительно равен 550, x и y - координаты мячика в заданные моменты времени, t– заданное время.
В ячейку С6 ввели формулу:
=$C$2*B6*COS(РАДИАНЫ($C$3))
Далее формула была скопирована на диапазоне С6:С21 А в ячейку D6 — формулу:
=$C$2*B6*SIN(РАДИАНЫ($3))-(9,8*B6^2/2)
Далее формула была скопирована на диапазоне D6:D21 [40].
Учитель: ребята, когда мы ввели все значения, что мы должны сделать дальше (построить диаграмму, чтобы посмотреть траекторию движения мя- чика). Она уже построена поэтому посмотрим, удовлетворяет ли она условию задачи.
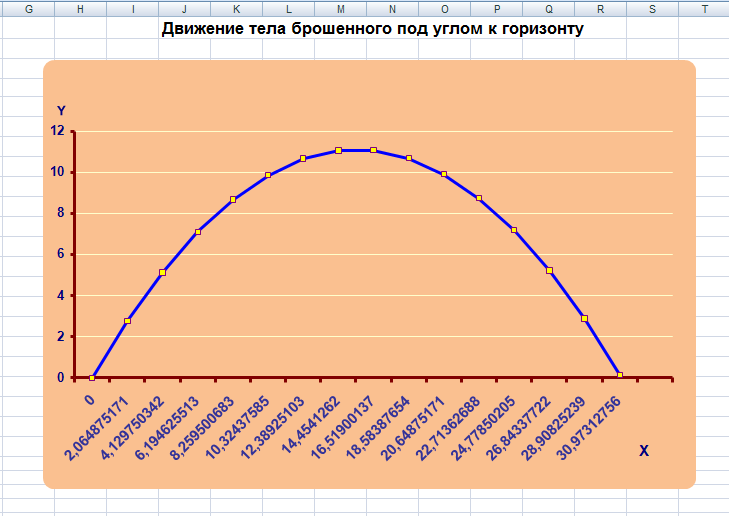 Диаграмма построена по типу «График» для визуализации траектории движения мячика, рис. 5.
Диаграмма построена по типу «График» для визуализации траектории движения мячика, рис. 5.
Рис. 5. График для визуализации траектории движения мячика Учитель: какой следующий этап проводим (компьютерный экспери-
мент).
На этапе компьютерного эксперимента у данной модели возникают проблемы со считыванием результатов эксперимента. При изменении угла броска мячика (значения ячейки С3) невозможно точно зарегистрировать по- падание мячиком в площадку. А при углах более 55 градусов требуется уве- личение диапазона данных и корректировка диаграммы, так как время полета мячика становится больше 3 секунд (то есть превышает первоначально за- данный диапазон) [18].
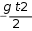
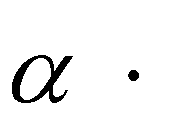 Учитель: очевидно, что необходима коррекция модели. На каком этапе
Учитель: очевидно, что необходима коррекция модели. На каком этапе
еѐ нужно проводить? (формализации). Так как требуется отступить от клас- сического подхода в описании модели процесса, как функции от времени, необходимо описать модель процесса как функцию от координаты х, учиты- вая особенности построения диаграмм в Microsoft Excel. Учащиеся записывают формулы в тетрадь.

 y V0
y V0
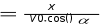 t
t
sin( ) t ,
Учитель: ребята откройте следующий файл под названием «Модель 2».
В этой модели внесены корректировки, рассмотрим их.
В ячейку В6 ввели формулу:
=C6/$C$2/COS(РАДИАНЫ($C$3))
Далее формула была скопирована на диапазоне В6:В41 А в ячейку D6 — формулу:
=$C$2*B6*SIN(РАДИАНЫ($C$3))-(9,8*B6^2/2).
Далее формула была скопирована на диапазоне D6:D41.
С целью визуализировать не только траекторию движения мячика, но и зону, в которую требуется попасть, был введен дополнительный ряд значе- ний у2,, рис. 6.
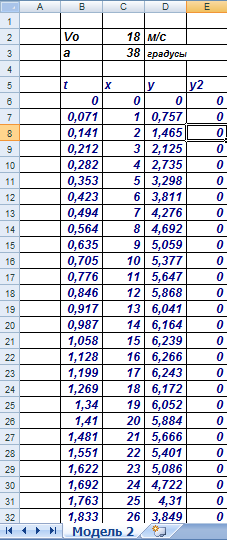
Рис. 6. Компьютерная модель «Движение тела брошенного под углом» в программе Microsoft Excel после корректировки
Учитель: построение диаграммы также изменилось. Был выбран другой тип диаграммы - «Точечная». После построения диаграммы точки х=30, х=31 и х=32 ряда у2. были выделены красным цветом и соответствующей формой маркеров, рис. 7.
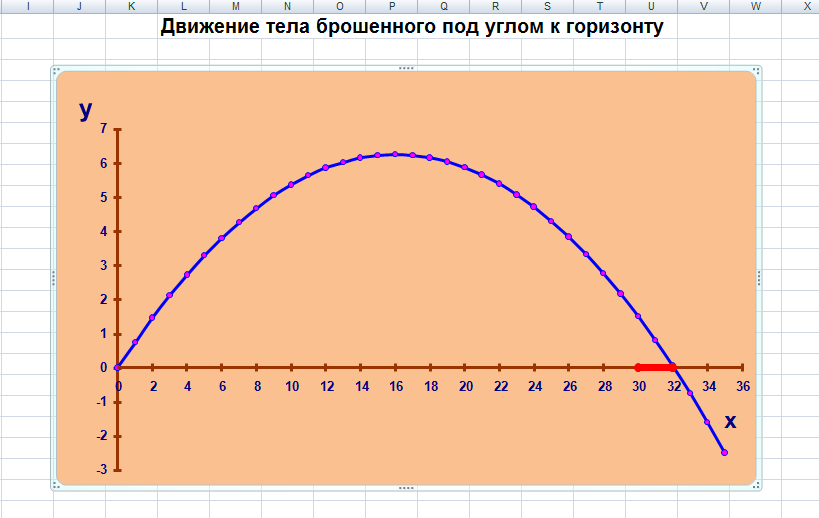
Рис. 7. Траектории движения мячика
Построенная диаграмма позволила считывать результаты компьютер- ного эксперимента с достаточной точностью.
Учитель: понравилось ли вам построение и исследование модели? На каком этапе у вас возникло затруднение и почему? Все ли этапы были прой-
дены? ( Нет, анализ полученных результатов после выполнения корректиров- ки не был пройден).
Итак, ребята, сегодня вы научились исследовать физическую модель средством Microsoft Excel.
7. Задание на дом.
Учитель: в тетрадях нужно описать:
 анализ полученных результатов
анализ полученных результатов  практическую значимость
практическую значимость
 вывод
вывод
Примерное выполнение домашнего задания Исследование модели и анализ полученных результатов.
При скорости V0=18 м/с зарегистрированы попадания в зону 30 – 32 метра от точки броска при углах: 33° – 38° и 52° – 57°
Результат был получен путем изменения значений ячейки С3 без до- полнительных коррекций области данных и диаграммы.
Практическая значимость.
В дальнейшем наша модель может быть использована на практических занятиях по информатике при изучении темы «Моделирование» в 9 классе и на уроках физики при изучении темы «Движение тел».
Выводы.
Проблемы в считывании результатов компьютерного эксперимента устранены путем коррекции модели на этапе формализованной записи и по- строения новой компьютерной модели на этапе преобразования формализо- ванной модели в компьютерную. Цель достигнута.
Учитель: что мы делаем на первом этапе построения модели? (изобра- жаем описательную информационную модель: «визуализация траектории движения тела, брошенного под углом к горизонту»).
Учитель вызывает учащегося к интерактивной доске выполнять первый этап построения, изображать модель, остальные выполняют в тетрадях.
С помощью фона «Сетка» и инструмента «умного пера» учащийся изображает условие задачи рис. 3.
 (v0 – начальная скорость, α – угол бросания, х – координата дальности полѐта, y – координата высоты полета, от времени).
(v0 – начальная скорость, α – угол бросания, х – координата дальности полѐта, y – координата высоты полета, от времени).Рис. 3. Движение тела, брошенного под углом к горизонту Учащийся присаживается на место.
Учитель: сформулируем основные предположения:
Учитель: теперь нашу информационную модель мы должны предста- вить в формализованную модель в нашем случае математическую. Что для этого мы используем? (формулы равномерного и равноускоренного движе- ния). Записываем все формулы в тетрадь.
cos( ) t
sin( ) t
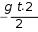
sin( )
g t ) 0 2
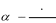
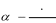
0 2
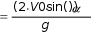 t
tУчитель: что мы делаем с получившийся формулой? (Подставляем по- лученное выражение для времени в формулу для вычисления координаты x). (Слайд 6)
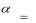
x 0 0 0
g g
Учитель: что мы делаем на третьем этапе? (на третьем этапе осуществ- ляем реализацию формализованной модели в компьютерную модель рис. 4. средствами ИКТ, в нашем случае с помощью электронной таблицы).
Учащиеся пересаживаются за компьютеры, открывают заранее подго- товленную учителем компьютерную модель в программе Microsoft Excel под названием «Модель1», рис. 4. Вместе с учителем рассматривают данные в модели.

Рис. 4. Компьютерная модель «Движение тела брошенного под углом» в про- грамме Microsoft Excel
Учитель: ребята расскажите, что дано в программе (v0 – начальная ско- рость равна приблизительно 18 м/с, α – угол бросания приблизительно равен 550, x и y - координаты мячика в заданные моменты времени, t– заданное время.
В ячейку С6 ввели формулу:
=$C$2*B6*COS(РАДИАНЫ($C$3))
Далее формула была скопирована на диапазоне С6:С21 А в ячейку D6 — формулу:
=$C$2*B6*SIN(РАДИАНЫ($3))-(9,8*B6^2/2)
Далее формула была скопирована на диапазоне D6:D21 [40].
Учитель: ребята, когда мы ввели все значения, что мы должны сделать дальше (построить диаграмму, чтобы посмотреть траекторию движения мя- чика). Она уже построена поэтому посмотрим, удовлетворяет ли она условию задачи.
 Диаграмма построена по типу «График» для визуализации траектории движения мячика, рис. 5.
Диаграмма построена по типу «График» для визуализации траектории движения мячика, рис. 5.Рис. 5. График для визуализации траектории движения мячика Учитель: какой следующий этап проводим (компьютерный экспери-
мент).
На этапе компьютерного эксперимента у данной модели возникают проблемы со считыванием результатов эксперимента. При изменении угла броска мячика (значения ячейки С3) невозможно точно зарегистрировать по- падание мячиком в площадку. А при углах более 55 градусов требуется уве- личение диапазона данных и корректировка диаграммы, так как время полета мячика становится больше 3 секунд (то есть превышает первоначально за- данный диапазон) [18].
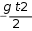
еѐ нужно проводить? (формализации). Так как требуется отступить от клас- сического подхода в описании модели процесса, как функции от времени, необходимо описать модель процесса как функцию от координаты х, учиты- вая особенности построения диаграмм в Microsoft Excel. Учащиеся записывают формулы в тетрадь.
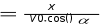 t
tsin( ) t ,
Учитель: ребята откройте следующий файл под названием «Модель 2».
В этой модели внесены корректировки, рассмотрим их.
В ячейку В6 ввели формулу:
=C6/$C$2/COS(РАДИАНЫ($C$3))
Далее формула была скопирована на диапазоне В6:В41 А в ячейку D6 — формулу:
=$C$2*B6*SIN(РАДИАНЫ($C$3))-(9,8*B6^2/2).
Далее формула была скопирована на диапазоне D6:D41.
С целью визуализировать не только траекторию движения мячика, но и зону, в которую требуется попасть, был введен дополнительный ряд значе- ний у2,, рис. 6.

Рис. 6. Компьютерная модель «Движение тела брошенного под углом» в программе Microsoft Excel после корректировки
Учитель: построение диаграммы также изменилось. Был выбран другой тип диаграммы - «Точечная». После построения диаграммы точки х=30, х=31 и х=32 ряда у2. были выделены красным цветом и соответствующей формой маркеров, рис. 7.

Рис. 7. Траектории движения мячика
Построенная диаграмма позволила считывать результаты компьютер- ного эксперимента с достаточной точностью.
-
Подведение итогов урока (рефлексия).
Учитель: понравилось ли вам построение и исследование модели? На каком этапе у вас возникло затруднение и почему? Все ли этапы были прой-
дены? ( Нет, анализ полученных результатов после выполнения корректиров- ки не был пройден).
Итак, ребята, сегодня вы научились исследовать физическую модель средством Microsoft Excel.
7. Задание на дом.
Учитель: в тетрадях нужно описать:
Примерное выполнение домашнего задания Исследование модели и анализ полученных результатов.
При скорости V0=18 м/с зарегистрированы попадания в зону 30 – 32 метра от точки броска при углах: 33° – 38° и 52° – 57°
Результат был получен путем изменения значений ячейки С3 без до- полнительных коррекций области данных и диаграммы.
Практическая значимость.
В дальнейшем наша модель может быть использована на практических занятиях по информатике при изучении темы «Моделирование» в 9 классе и на уроках физики при изучении темы «Движение тел».
Выводы.
Проблемы в считывании результатов компьютерного эксперимента устранены путем коррекции модели на этапе формализованной записи и по- строения новой компьютерной модели на этапе преобразования формализо- ванной модели в компьютерную. Цель достигнута.