Добавлен: 11.01.2024
Просмотров: 142
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Глава ІІ. Математическое моделирование – один из основных
методов решения текстовых задач в основной школе
2.1. Понятие модели и моделирования
Для решения многих научных и практических задач широко используется метод моделирования. Реальные объекты или процессы иногда бывают настолько сложны и многогранны, что их изучение невозможно без построения и исследования модели, отображающей лишь какую-то сторону этого процесса или объекта и потому более простую, чем эта реальность.
Под моделью (от лат. тodе1u — мера) понимают мысленно представимую или материально реализованную систему, которая, отражая и воспроизводя объект исследования, способна замещать его при определенных условиях так, что изучение ее дает новую информацию об этом объекте.
Все математические понятия, такие, как число, функция, уравнение, геометрическая фигура и др. представляют собой особые модели количественных отношений и пространственных форм окружающей действительности.
Эти модели математика сконструировала в процессе своего многовекового развития. Но и в настоящее время продолжается конструиро-вание различных математических моделей, и любое творчество в области математики связано с созданием новых моделей. Для изучения этих моделей в математике разработаны многочисленные методы, такие, как методы решения уравнений, исследования функций, измерения и вычисление длин, площадей и объемов геометрических фигур и тел и т.д. Наконец, в математике разработаны и особы методики для использования в практике результатов исследования математических моделей. Примером такой методики являются приемы решения практических задач с помощью уравнений.
Однако, обнаруживается такой парадокс: то, что они имеют дело с моделями, изучают модели, учащиеся, как правило, не знают. Да и откуда им это знать, если в программах и учебниках эти понятия почти отсутствуют? Учащиеся в 9 классе с удивлением узнают, что привычные для них понятия, уравнения, числа, фигуры являются научными моделями, что, решая задачи, они моделируют.
На первом уроке темы «Математическое моделирование» учащиеся в ответ на вопрос "Что такое модель и моделирование?" не дав четкого определения, указали лишь на модели геометрических тел; моделирование они определяли как процесс построения таких моделей. Отвечая на вопрос "Где и для чего используется моделирование?» школьники опять-таки ссылались на те же модели геометрических тел. На вопрос "Какова роль моделирования в науке?" дети либо вовсе не смогли дать ответа, либо ограничивались указанием на роль моделей как наглядных образов.
В системе обучения решению задач (текстовых, сюжетных), в основе которой лежало широкое использование моделирования задачи рассматривались как особые знаковые модели реальных ситуаций (задачных ситуаций), а процесс их решения - как построение цепи моделей (вспомогательной, обобщенной предметной, логической математической и др.).
2.2. Методы решения задач
Существуют различные методы решения текстовых задач: арифметический, алгебраический, геометрический, логический, практический и др. В основе каждого метода лежат различные виды математических моделей. Например, при алгебраическом методе решения задачи составляют-ся уравнения или неравенства, при геометрическом — строятся диаграммы или графики. Решение задачи логическим методом начинается с составления алгоритма.
Следует иметь в виду, что практически каждая задача в рамках выбранного метода допускает решение с помощью различных моделей. Так, используя алгебраический метод, ответ на требование одной и той же задачи можно получить, составив и решив совершенно разные уравнения, используя логический метод — построив разные алгоритмы. Ясно, что и в этих случаях мы также имеем дело с различными методами решения конкретной задачи, которые (с целью избежать разночтения и неоднозначность трактовки термина «метод решения») будем называть способами решения.
Иногда для краткости изложения вместо того чтобы говорить, что зада-ча решена определенным способом в рамках, например, арифметического метода, будем говорить, что «задача решена арифметическим способом» или «задача решена арифметическим методом», а то и просто — «задача решена арифметически».
Арифметический метод. Решить задачу арифметическим методом — значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту же задачу во многих случаях можно решить различными арифметическими способами. Задача считается решенной различными способами, если ее решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью использования этих связей.
Задача. Поют в хоре и занимаются танцами 82 студента, занимаются танцами и художественной гимнастикой 32 студента, а поют в хоре и занимаются художественной гимнастикой 78 студентов. Сколько студентов поют в хоре, занимаются танцами и художественной гимнастикой отдельно, если известно, что каждый студент занимается только чем-то одним?
Решение.
1-й способ.
1) 82 + 32 + 78 = 192 (чел.) — удвоенное число студентов, поющих в хоре, занимающихся танцами и художественной гимнастикой;
2) 192 : 2 = 96 (чел.) — поют в хоре, занимаются танцами и художественной гимнастикой;
3) 96 – 32 = 64 (чел.) — поют в хоре;
4) 96 - 78 = 18 (чел.) — занимаются танцами;
5) 96 - 82 = 14 (чел.) — занимаются художественной гимнастикой.
2-й способ.
1) 82 - 32 = 50 (чел.) — на столько больше студентов поют в хоре, чем занимаются художественной гимнастикой;
2) 50 + 78 = 128 (чел.) — удвоенное число студентов, поющих в хоре;
3) 128 : 2 = 64 (чел.) — поют в хоре;
4) 78 - 64 = 14 (чел.) — занимаются художественной гимнастикой;
5) 82 - 64 18 (чел.) — занимаются танцами.
Ответ: 64 студента поют в хоре, 14 студентов занимаются художественной гимнастикой, 18 студентов занимаются танцами.
Алгебраический метод. Решить задачу алгебраическим методом — это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений (или неравенств). Одну и ту же задачу можно также решить различными алгебраическими способами. Задача считается решенной различными способами, если для ее решения составлены различные уравнения или системы уравнений (неравенств), в основе составления которых лежат различные соотношения между данными и искомыми.
Задача. Рабочий может сделать определенное число деталей за три дня. Если он в день будет делать на 10 деталей больше, то справится с заданием за два дня. Какова первоначальная производительность рабочего и сколько деталей он должен сделать?
Решение.
1-й способ.
Пусть х д./день — первоначальная производительность рабочего. Тогда (х + 10) д./день — новая производительность, 3х д. — число деталей, которые он должен сделать. По условию получаем уравнение 3х = 2(х + 10), решив которое найдемх = 20. Первоначальная производительность рабочего 20 деталей в день, он должен сделать 60 деталей.
2-й способ.
Пусть х д. — число деталей, которые должен сделать рабочий. Тогда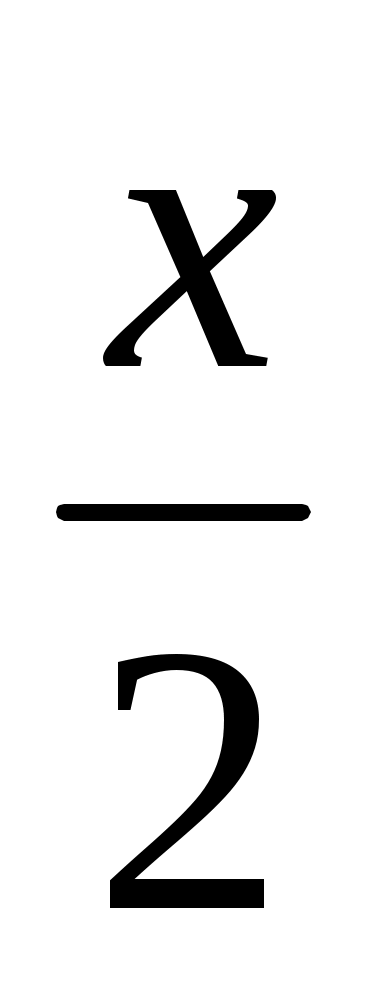
— новая производительность, 
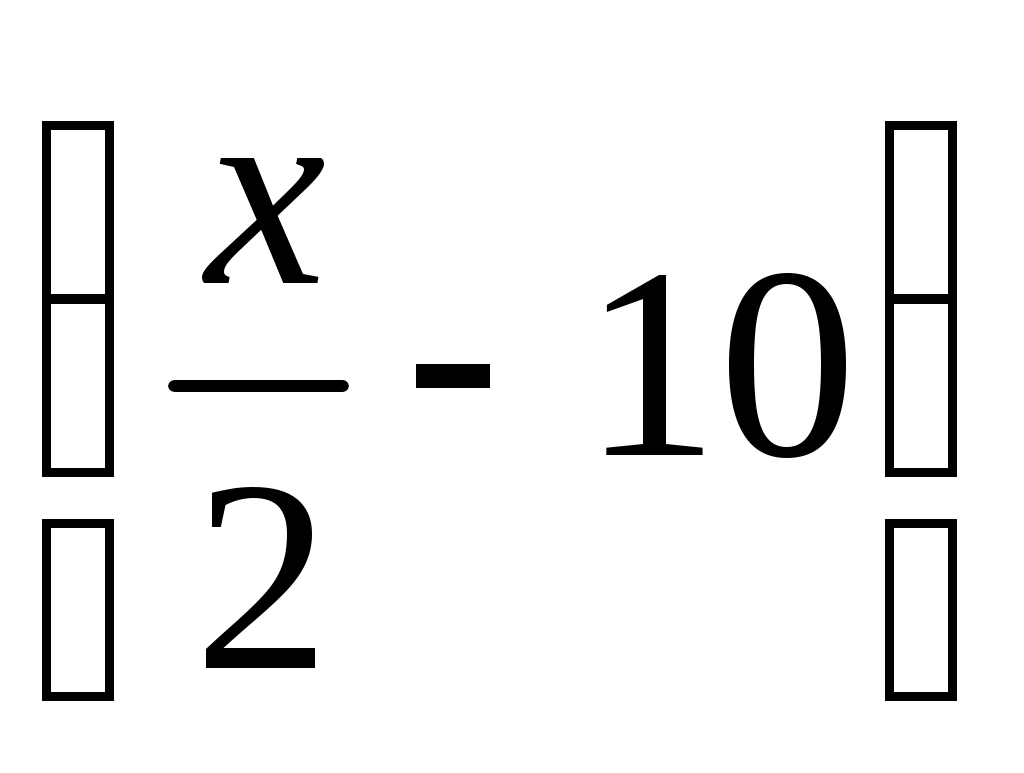д./день — первоначальная производительность рабочего. По условию получаем уравнение
х = 3
, решив которое найдем х = 60. Рабочий должен сделать 60 деталей, его первоначальная производительность 20 деталей в день.
Ответ: 20 деталей в день; 60 деталей.
Аналитико-Геометрический метод. Решить задачу аналитико-геометрическим методом — значит найти ответ на требование задачи, используя как алгебраические выражения, уравнения, неравенства, системы уравнений и неравенств так и геометрические построения или свойства геометрических фигур. Одну и ту же задачу можно также решить различными геометрическими способами. Задача считается решенной различными способами, если для ее решения используются различные построения или свойства фигур.
Задача. Из двух городов А и В, расстояние между которыми 250 км, навстречу друг другу выехали два туриста. Скорость движения первого равна 20 км/ч, второго — 30 км/ч. Через сколько часов туристы встретятся?
Решение.
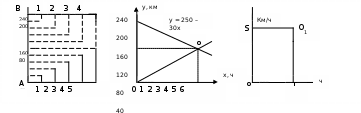
1-й способ. Математическую модель задачи представим в виде диаграммы. Примем длину одного отрезка по вертикали за 10 км, а длину одного отрезка по горизонтали — за 1 ч. Отложим на вертикальной прямой отрезок АВ равный 250 км. Он будет изображать расстояние между городами. Для удобства проведем еще одну ось времени через точку 6. Затем на вертикаль-ных прямых станем откладывать отрезки пути, пройденные каждым туристом за 1 ч, 2ч, 3ч. и т. д.(рис 1. а). Из чертежа видим, что через 5 ч они встретятся.
2-й способ. В прямоугольной системе координат по горизонтали отложим время движения (в часах), по вертикали — расстояние (в километрах). Примем длину одного отрезка по вертикали за 10 км, а длину одного отрезка по горизонтали — за 1 ч. Построим графики, характеризующие движение каждого туриста. Движение первого туриста определяется функцией у = 20х, второго — у = 250 – 30х. Абсцисса точки их пересечения (точки О) указывает, через сколько часов туристы встретятся (рис 1.б). Из чертежа видно, что ее значение равно 5. Ордината указывает, на каком расстоянии от пункта А произойдет встреча. Ее значение равно 100.
3-й способ. Пусть время движения туристов до встречи изображается отрезком ОТ, а скорость сближения—отрезком 0S. (рис 1. в). Тогда площадь S прямоугольника 0S0
Т (она равна 0S · ОТ) соответствует расстоянию между городами
А и В (пройденный путь есть произведение скорости движения на время движения). Учитывая, что туристы сближаются каждый час на 20 + 30 = 50 (км), расстояние между городами равно 250 км, имеем уравнение
250 = 50 · ОТ, решив которое находим ОТ = 5 (ч). Итак, туристы встретятся через 5 ч.
Ответ: через 5 ч.
5
Рис.1. а б в
Практический метод. Решить задачу практическим методом — значит найти ответ на требование задачи, выполнив практические действия с предметами или их копиями (моделями, макетами и т.п.).
Задача. Некто истратил 30 грн. своих денег, после чего удвоил оставшиеся деньги. Затем он истратил 60 грн., после чего опять удвоил оставшиеся деньги. Когда он еще истратил 90 грн., у него осталось 70 грн. Сколько денег было вначале?
Решение.
Чтобы определить, сколько денег было первоначально, возьмем оставшееся количество денег и выполним обратные операции в обратном порядке. Берем оставшиеся 70 грн., добавляем к ним истраченные 90 грн. (160 грн.), затем делим эту сумму пополам и узнаем, сколько денег было до того, как второй раз удвоили оставшиеся деньги (80 грн.). После этого добавляем 60 грн. и находим, сколько денег было до того, как истратили 60 грн. (140 . грн). Делим эту сумму пополам и узнаем, сколько денег было до того, как первый раз удвоили оставшиеся деньги (70 грн.), прибавляем истраченные в первый раз 30 грн. и находим первоначальное количество денег (100 грн).
Ответ: первоначально было 100 грн.
Иногда в ходе решения задачи применяются несколько методов: алгебраический и арифметический; геометрический, алгебраический и арифметический; арифметический и практический и т. п. В этом случае считают, что задача решается комбинированным (смешанным) методом.
Задача. Четыре товарища купили телевизор. Первый внес половину суммы, вносимой остальными, второй — треть того, что внесли все его товарищи, третий — четверть того, что все его товарищи, четвертый — оставшиеся 650 р. Сколько было уплачено за телевизор?
Решение. Пусть первый товарищ внес х грн., второй — у грн., третий — z грн. Тогда, решая задачу чисто алгебраическим методом, по условию задачи получим достаточно громоздкую систему трех уравнений с тремя неизвестными:
методов решения текстовых задач в основной школе
2.1. Понятие модели и моделирования
Для решения многих научных и практических задач широко используется метод моделирования. Реальные объекты или процессы иногда бывают настолько сложны и многогранны, что их изучение невозможно без построения и исследования модели, отображающей лишь какую-то сторону этого процесса или объекта и потому более простую, чем эта реальность.
Под моделью (от лат. тodе1u — мера) понимают мысленно представимую или материально реализованную систему, которая, отражая и воспроизводя объект исследования, способна замещать его при определенных условиях так, что изучение ее дает новую информацию об этом объекте.
Все математические понятия, такие, как число, функция, уравнение, геометрическая фигура и др. представляют собой особые модели количественных отношений и пространственных форм окружающей действительности.
Эти модели математика сконструировала в процессе своего многовекового развития. Но и в настоящее время продолжается конструиро-вание различных математических моделей, и любое творчество в области математики связано с созданием новых моделей. Для изучения этих моделей в математике разработаны многочисленные методы, такие, как методы решения уравнений, исследования функций, измерения и вычисление длин, площадей и объемов геометрических фигур и тел и т.д. Наконец, в математике разработаны и особы методики для использования в практике результатов исследования математических моделей. Примером такой методики являются приемы решения практических задач с помощью уравнений.
Однако, обнаруживается такой парадокс: то, что они имеют дело с моделями, изучают модели, учащиеся, как правило, не знают. Да и откуда им это знать, если в программах и учебниках эти понятия почти отсутствуют? Учащиеся в 9 классе с удивлением узнают, что привычные для них понятия, уравнения, числа, фигуры являются научными моделями, что, решая задачи, они моделируют.
На первом уроке темы «Математическое моделирование» учащиеся в ответ на вопрос "Что такое модель и моделирование?" не дав четкого определения, указали лишь на модели геометрических тел; моделирование они определяли как процесс построения таких моделей. Отвечая на вопрос "Где и для чего используется моделирование?» школьники опять-таки ссылались на те же модели геометрических тел. На вопрос "Какова роль моделирования в науке?" дети либо вовсе не смогли дать ответа, либо ограничивались указанием на роль моделей как наглядных образов.
В системе обучения решению задач (текстовых, сюжетных), в основе которой лежало широкое использование моделирования задачи рассматривались как особые знаковые модели реальных ситуаций (задачных ситуаций), а процесс их решения - как построение цепи моделей (вспомогательной, обобщенной предметной, логической математической и др.).
2.2. Методы решения задач
Существуют различные методы решения текстовых задач: арифметический, алгебраический, геометрический, логический, практический и др. В основе каждого метода лежат различные виды математических моделей. Например, при алгебраическом методе решения задачи составляют-ся уравнения или неравенства, при геометрическом — строятся диаграммы или графики. Решение задачи логическим методом начинается с составления алгоритма.
Следует иметь в виду, что практически каждая задача в рамках выбранного метода допускает решение с помощью различных моделей. Так, используя алгебраический метод, ответ на требование одной и той же задачи можно получить, составив и решив совершенно разные уравнения, используя логический метод — построив разные алгоритмы. Ясно, что и в этих случаях мы также имеем дело с различными методами решения конкретной задачи, которые (с целью избежать разночтения и неоднозначность трактовки термина «метод решения») будем называть способами решения.
Иногда для краткости изложения вместо того чтобы говорить, что зада-ча решена определенным способом в рамках, например, арифметического метода, будем говорить, что «задача решена арифметическим способом» или «задача решена арифметическим методом», а то и просто — «задача решена арифметически».
Арифметический метод. Решить задачу арифметическим методом — значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту же задачу во многих случаях можно решить различными арифметическими способами. Задача считается решенной различными способами, если ее решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью использования этих связей.
Задача. Поют в хоре и занимаются танцами 82 студента, занимаются танцами и художественной гимнастикой 32 студента, а поют в хоре и занимаются художественной гимнастикой 78 студентов. Сколько студентов поют в хоре, занимаются танцами и художественной гимнастикой отдельно, если известно, что каждый студент занимается только чем-то одним?
Решение.
1-й способ.
1) 82 + 32 + 78 = 192 (чел.) — удвоенное число студентов, поющих в хоре, занимающихся танцами и художественной гимнастикой;
2) 192 : 2 = 96 (чел.) — поют в хоре, занимаются танцами и художественной гимнастикой;
3) 96 – 32 = 64 (чел.) — поют в хоре;
4) 96 - 78 = 18 (чел.) — занимаются танцами;
5) 96 - 82 = 14 (чел.) — занимаются художественной гимнастикой.
2-й способ.
1) 82 - 32 = 50 (чел.) — на столько больше студентов поют в хоре, чем занимаются художественной гимнастикой;
2) 50 + 78 = 128 (чел.) — удвоенное число студентов, поющих в хоре;
3) 128 : 2 = 64 (чел.) — поют в хоре;
4) 78 - 64 = 14 (чел.) — занимаются художественной гимнастикой;
5) 82 - 64 18 (чел.) — занимаются танцами.
Ответ: 64 студента поют в хоре, 14 студентов занимаются художественной гимнастикой, 18 студентов занимаются танцами.
Алгебраический метод. Решить задачу алгебраическим методом — это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений (или неравенств). Одну и ту же задачу можно также решить различными алгебраическими способами. Задача считается решенной различными способами, если для ее решения составлены различные уравнения или системы уравнений (неравенств), в основе составления которых лежат различные соотношения между данными и искомыми.
Задача. Рабочий может сделать определенное число деталей за три дня. Если он в день будет делать на 10 деталей больше, то справится с заданием за два дня. Какова первоначальная производительность рабочего и сколько деталей он должен сделать?
Решение.
1-й способ.
Пусть х д./день — первоначальная производительность рабочего. Тогда (х + 10) д./день — новая производительность, 3х д. — число деталей, которые он должен сделать. По условию получаем уравнение 3х = 2(х + 10), решив которое найдемх = 20. Первоначальная производительность рабочего 20 деталей в день, он должен сделать 60 деталей.
2-й способ.
Пусть х д. — число деталей, которые должен сделать рабочий. Тогда
— новая производительность, д./день — первоначальная производительность рабочего. По условию получаем уравнение
х = 3
, решив которое найдем х = 60. Рабочий должен сделать 60 деталей, его первоначальная производительность 20 деталей в день.Ответ: 20 деталей в день; 60 деталей.
Аналитико-Геометрический метод. Решить задачу аналитико-геометрическим методом — значит найти ответ на требование задачи, используя как алгебраические выражения, уравнения, неравенства, системы уравнений и неравенств так и геометрические построения или свойства геометрических фигур. Одну и ту же задачу можно также решить различными геометрическими способами. Задача считается решенной различными способами, если для ее решения используются различные построения или свойства фигур.
Задача. Из двух городов А и В, расстояние между которыми 250 км, навстречу друг другу выехали два туриста. Скорость движения первого равна 20 км/ч, второго — 30 км/ч. Через сколько часов туристы встретятся?
Решение.
1-й способ. Математическую модель задачи представим в виде диаграммы. Примем длину одного отрезка по вертикали за 10 км, а длину одного отрезка по горизонтали — за 1 ч. Отложим на вертикальной прямой отрезок АВ равный 250 км. Он будет изображать расстояние между городами. Для удобства проведем еще одну ось времени через точку 6. Затем на вертикаль-ных прямых станем откладывать отрезки пути, пройденные каждым туристом за 1 ч, 2ч, 3ч. и т. д.(рис 1. а). Из чертежа видим, что через 5 ч они встретятся.
2-й способ. В прямоугольной системе координат по горизонтали отложим время движения (в часах), по вертикали — расстояние (в километрах). Примем длину одного отрезка по вертикали за 10 км, а длину одного отрезка по горизонтали — за 1 ч. Построим графики, характеризующие движение каждого туриста. Движение первого туриста определяется функцией у = 20х, второго — у = 250 – 30х. Абсцисса точки их пересечения (точки О) указывает, через сколько часов туристы встретятся (рис 1.б). Из чертежа видно, что ее значение равно 5. Ордината указывает, на каком расстоянии от пункта А произойдет встреча. Ее значение равно 100.
3-й способ. Пусть время движения туристов до встречи изображается отрезком ОТ, а скорость сближения—отрезком 0S. (рис 1. в). Тогда площадь S прямоугольника 0S0
Т (она равна 0S · ОТ) соответствует расстоянию между городами
А и В (пройденный путь есть произведение скорости движения на время движения). Учитывая, что туристы сближаются каждый час на 20 + 30 = 50 (км), расстояние между городами равно 250 км, имеем уравнение
250 = 50 · ОТ, решив которое находим ОТ = 5 (ч). Итак, туристы встретятся через 5 ч.
Ответ: через 5 ч.
5
Рис.1. а б в
Практический метод. Решить задачу практическим методом — значит найти ответ на требование задачи, выполнив практические действия с предметами или их копиями (моделями, макетами и т.п.).
Задача. Некто истратил 30 грн. своих денег, после чего удвоил оставшиеся деньги. Затем он истратил 60 грн., после чего опять удвоил оставшиеся деньги. Когда он еще истратил 90 грн., у него осталось 70 грн. Сколько денег было вначале?
Решение.
Чтобы определить, сколько денег было первоначально, возьмем оставшееся количество денег и выполним обратные операции в обратном порядке. Берем оставшиеся 70 грн., добавляем к ним истраченные 90 грн. (160 грн.), затем делим эту сумму пополам и узнаем, сколько денег было до того, как второй раз удвоили оставшиеся деньги (80 грн.). После этого добавляем 60 грн. и находим, сколько денег было до того, как истратили 60 грн. (140 . грн). Делим эту сумму пополам и узнаем, сколько денег было до того, как первый раз удвоили оставшиеся деньги (70 грн.), прибавляем истраченные в первый раз 30 грн. и находим первоначальное количество денег (100 грн).
Ответ: первоначально было 100 грн.
Иногда в ходе решения задачи применяются несколько методов: алгебраический и арифметический; геометрический, алгебраический и арифметический; арифметический и практический и т. п. В этом случае считают, что задача решается комбинированным (смешанным) методом.
Задача. Четыре товарища купили телевизор. Первый внес половину суммы, вносимой остальными, второй — треть того, что внесли все его товарищи, третий — четверть того, что все его товарищи, четвертый — оставшиеся 650 р. Сколько было уплачено за телевизор?
Решение. Пусть первый товарищ внес х грн., второй — у грн., третий — z грн. Тогда, решая задачу чисто алгебраическим методом, по условию задачи получим достаточно громоздкую систему трех уравнений с тремя неизвестными: