ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 84
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ся построить условную развертку по-верхности вращения (рис. 13.11). При построении услов-ной развертки способомцилиндровданная поверхность мысленно разрезается меридиональными плоскостями Г, Г′,… (то есть плоскостями, проходящими через ее ось вращения), на несколько равных частей (рис. 13.12, а). Каждая часть заменяется отсеком цилиндрической по-верхности Ф, которая касается заданной поверхности вдоль ее меридиана m. В результате поверхность враще-ния приближенно заменяется (аппроксимируется) состав-
ной поверхностью, состоящей из одинаковых цилиндри- Рис. 13.11 ческих “лепестков” Фс горизонтальными образующими.
Каждый лепесток можно приближенно развернуть на плоскость. Совокупность развер-ток всех лепестков составляет условную развертку поверхности вращения.
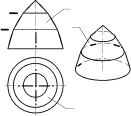
При построении условной развертки поверхности вращения способомконусовдан-ная поверхность, как и при использовании способа цилиндров, мысленно разрезается на несколько частей. Но секущие плоскости Σ, Σ′,… проводят не через ось вращения, а перпендикулярно ей. Вся поверхность делится секущими плоскостями на несколько горизонтальных “поясков”
(рис. 13.12, б). Каждый поясок заменяется отсеком кониче-ской поверхности Θ. В результате заданная поверхность вращения приближенно заме-няется (аппроксимируется) составной поверхностью, состоящей из разных конических поясков Θ, стыкующихся между собой по параллелям данной поверхности вращения.
Каждый конический поясок, представляющий собой поверхность усеченного кругового конуса, можно развернуть на плоскость. Совокупность разверток всех поясков со-ставляет условную развертку поверхности.

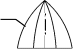
 Ф2= m2 Σ2 Θ2Σ′2Θ
Ф2= m2 Σ2 Θ2Σ′2Θ
 Г′1
Г′1
Ф1m1 Ф
 Г1
Г1
Θ1
а) б) Рис. 13.12
Рассмотрим конструктивное построение условной развертки неразвертывающейся поверхности вращения способом цилиндров и способом конусов.
13.3.2.1. Способ цилиндров
Данную поверхность вращения мысленно разрезаем меридиональными плоскостя-ми Г, Г′,… на равные участки (рис.
13.13, а). Развертки одинаковых участков поверхно-
m2 D2 S2
 C2
C2
B2
12=22=A2
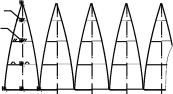 D S
D S
C
B
Г1′
 11 B1
11 B1
A1
C1 D1 1 A 2
S1
 Г1 21 m1
Г1 21 m1
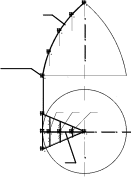
Заменим выделенный участок поверхности вращения участком (отсеком) Фцилин-дрической поверхности, касающейся заменяемого участка вдоль среднего меридиана m. Меридиан mрасположен во фронтальной плоскости уровня, поэтому дуга ASмеридиа-на m изображается на П2в натуральную величину.
Цилиндрический отсек Ф, как и выделенный участок поверхности вращения, огра-ничен плоскостями Г, Г′. Поверхность отсека Фзанимает фронтально-проецирующее положение, поэтому его фронтальная проекция совпадает на чертеже с фронтальной проекцией m2меридиана m. Горизонтальная проекция отсека Ф – треугольник 1121S1.
Таким образом, участок исходной поверхности вращения, ограниченный плоско-стями Г, Г′, приближенно заменяется (аппроксимируется) отсеком Фцилиндрической поверхности, ограниченным теми же плоско
стями Г, Г′. Направляющая линия поверх-ности Ф– меридиан m, являющийся одновременно нормальным сечением цилиндра Ф; образующие цилиндра Ф горизонтальны (см. рис. 13.13, а).
Для приближенного построения развертки отсека Фзаменяем направляющую m=ASломаной линией ABCDS, фронтальная проекция A2B2C2D2S2которой указывает истинную длину всех ее звеньев. В соответствии со способом нормального сечения, спрямляем ломаную линию A2B2C2D2S2в отрезок ABCDS, начерченный на свободном месте чертежа (рис. 13.13, б). Через точки A, B, C, Dпроводим прямые, перпендику-лярные AS, на которых откладываем отрезки касательных, проведенных к соответст-вующим параллелям. Эти отрезки ограничены плоскостями Г, Г′. Например, через точ-ку Aпроведен отрезок 1-2касательной к круговому основанию данного тела вращения, ограниченный плоскостями Г, Г′.
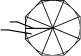
Соединяя концы отрезков касательных плавной кривой, получаем приближенную развертку одного цилиндрического “лепестка” 1-2-S. Полная условная развертка дан-ной поверхности вращения состоит из восьм
ной поверхностью, состоящей из одинаковых цилиндри- Рис. 13.11 ческих “лепестков” Фс горизонтальными образующими.
Каждый лепесток можно приближенно развернуть на плоскость. Совокупность развер-ток всех лепестков составляет условную развертку поверхности вращения.
При построении условной развертки поверхности вращения способомконусовдан-ная поверхность, как и при использовании способа цилиндров, мысленно разрезается на несколько частей. Но секущие плоскости Σ, Σ′,… проводят не через ось вращения, а перпендикулярно ей. Вся поверхность делится секущими плоскостями на несколько горизонтальных “поясков”
(рис. 13.12, б). Каждый поясок заменяется отсеком кониче-ской поверхности Θ. В результате заданная поверхность вращения приближенно заме-няется (аппроксимируется) составной поверхностью, состоящей из разных конических поясков Θ, стыкующихся между собой по параллелям данной поверхности вращения.
Каждый конический поясок, представляющий собой поверхность усеченного кругового конуса, можно развернуть на плоскость. Совокупность разверток всех поясков со-ставляет условную развертку поверхности.

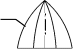
 Ф2= m2 Σ2 Θ2Σ′2Θ
Ф2= m2 Σ2 Θ2Σ′2Θ
 Г′1
Г′1Ф1m1 Ф
 Г1
Г1Θ1
а) б) Рис. 13.12
Рассмотрим конструктивное построение условной развертки неразвертывающейся поверхности вращения способом цилиндров и способом конусов.
13.3.2.1. Способ цилиндров
Данную поверхность вращения мысленно разрезаем меридиональными плоскостя-ми Г, Г′,… на равные участки (рис.
13.13, а). Развертки одинаковых участков поверхно-
m2 D2 S2
 C2
C2B2
12=22=A2
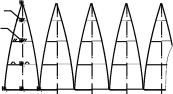 D S
D SC
B
Г1′
 11 B1
11 B1A1
C1 D1 1 A 2
S1
 Г1 21 m1
Г1 21 m1
1 2 3 4 5 6 7
а) б) Рис. 13.13
сти одинаковы, поэтому достаточно построить условную развертку лишь одного участ-ка. На рис. 13.13, аповерхность разрезана на 8 участков. Показан только один участок, выделенный плоскостями Г, Г′. Отмечен средний меридиан m=AS этого участка.
сти одинаковы, поэтому достаточно построить условную развертку лишь одного участ-ка. На рис. 13.13, аповерхность разрезана на 8 участков. Показан только один участок, выделенный плоскостями Г, Г′. Отмечен средний меридиан m=AS этого участка.
Заменим выделенный участок поверхности вращения участком (отсеком) Фцилин-дрической поверхности, касающейся заменяемого участка вдоль среднего меридиана m. Меридиан mрасположен во фронтальной плоскости уровня, поэтому дуга ASмеридиа-на m изображается на П2в натуральную величину.
Цилиндрический отсек Ф, как и выделенный участок поверхности вращения, огра-ничен плоскостями Г, Г′. Поверхность отсека Фзанимает фронтально-проецирующее положение, поэтому его фронтальная проекция совпадает на чертеже с фронтальной проекцией m2меридиана m. Горизонтальная проекция отсека Ф – треугольник 1121S1.
Таким образом, участок исходной поверхности вращения, ограниченный плоско-стями Г, Г′, приближенно заменяется (аппроксимируется) отсеком Фцилиндрической поверхности, ограниченным теми же плоско
стями Г, Г′. Направляющая линия поверх-ности Ф– меридиан m, являющийся одновременно нормальным сечением цилиндра Ф; образующие цилиндра Ф горизонтальны (см. рис. 13.13, а).
Для приближенного построения развертки отсека Фзаменяем направляющую m=ASломаной линией ABCDS, фронтальная проекция A2B2C2D2S2которой указывает истинную длину всех ее звеньев. В соответствии со способом нормального сечения, спрямляем ломаную линию A2B2C2D2S2в отрезок ABCDS, начерченный на свободном месте чертежа (рис. 13.13, б). Через точки A, B, C, Dпроводим прямые, перпендику-лярные AS, на которых откладываем отрезки касательных, проведенных к соответст-вующим параллелям. Эти отрезки ограничены плоскостями Г, Г′. Например, через точ-ку Aпроведен отрезок 1-2касательной к круговому основанию данного тела вращения, ограниченный плоскостями Г, Г′.
Соединяя концы отрезков касательных плавной кривой, получаем приближенную развертку одного цилиндрического “лепестка” 1-2-S. Полная условная развертка дан-ной поверхности вращения состоит из восьм