ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 83
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
оймногограннойпо-верхностьюФ′.Затемстроятточнуюразверткуаппроксимирующеймногогранной поверхности Ф′ и принимают ее за приближенную развертку данной поверхности Ф.
Хотя все остальные поверхности (не относящиеся к многогранным, цилиндриче-ским, коническим, торсовым) теоретически не развертываются на плоскость, инженер-ная практика, тем не менее, требует построения их “разверток”. Для неразвертываю-щихся поверхностей строят так называемые условные развертки.
13.1. Построение разверток поверхностей многогранников
Напомним, что многогранником называют пространственную геометрическую фи-гуру, со всех сторон ограниченную плоскими многоугольниками (гранями). Развертка многогранника представляет собой плоскую фигуру, которая получается при совмеще-нии граней многогранника с плоскостью. Процесс построения развертки поверхности многогранника сводится к построению истинных величин его граней, что непосредст-венно связано с определением натуральной (истинной) длины каждого ребра много-гранника. Рассмотрим построение разверток наиболее распространенных многогран-ных поверхностей – поверхностей пирамид и призм.
13.1.1. Развертка пирамиды
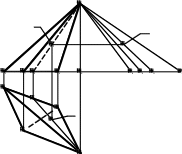
Поверхность n-угольной пирамиды включает в себя основание (плоский n-угольник) и боковую поверхность, состоящую из nтреугольников. Для построения раз-вертки пирамиды необходимо определить натуральные величины боковых ребер и сто-рон основания. На рис. 13.1, аизображена треугольная пирамида ABCS. Основанием
пирамиды является треугольник АВС, расположенный в плоскости,
параллельной гори-зонтальной плоскости проекций, поэтому стороны основания AB, BC, AC проецируются на П1в натуральную величину.
Длины боковых ребер пирамиды определяются с помощью вспомогательных пря-моугольных треугольников. Вспомогательные треугольники имеют общий катет S2O0(разность высот концов боковых ребер пирамиды). Другой катет равен длине горизон-тальной проекции соответствующего ребра. Например, в треугольнике S2O0A0катет S2O0равен разности высот точек Sи А. Другой катет O0А0равен горизонтальной проек-ции ребра SA: O0A0=S1A1. Истинная длина ребра SAравна величине гипотенузы S2A0. Аналогично длина ребра SB равна S2B0, а длина ребра SC равна S2C0.
 S2
S2
 K2 K0 A A 1
K2 K0 A A 1
A2 B
B2 12 C2 O0
A1 11 C1K1
C0B010 A0 K
A C
B1
S1
а)
Рис. 13.1
SK=S2K0
б) S
Развертка боковой поверхности пирамиды состоит из трех примыкающих друг к другу треугольников (рис. 13.1, б), конгруэнтных соответствующим граням пирамиды. Например, треугольник ACS(развертка соответствующей грани пирамиды) построен по известной длине стороны ACи найденным на рис. 13.1, адлинам боковых ребер пира-миды AS и CS. К развертке боковых граней пирамиды пристраиваем ее основание ABC.
Пусть на поверхности пирамиды отмечена точка K. Чтобы найти положение этой точки на развертке, проводим через Kвспомогательную прямую S-K-1, отмечаем на развертке точку 1и с помощью прямоугольного треугольника S2O010находим истин-ную длину отрезка SK=S2K0. Откладывая этот отрезок на развертке от точки Sвдоль прямой S-1, находим точку K.
13.1.2. Развертка призмы
На рис. 13.2, аизображена наклонная призма. Призма расположена таким образом, что ее основание параллельно горизонтальной плоскости проекций, поэтому на П1ос-нование ABCпризмы проецируется в натуральную величину A1B1C1. Боковые ребра призмы параллельны фронтальной плоскости проекций, поэтому на П2они проециру-ются без искажения.
Развертка боковой поверхности призмы может быть получена способомнормально-госечения.Для этого боковую поверхность призмы рассекают фронтально-
проецирующей плоскостью Σ, перпендикулярной боковым ребрам призмы. Истинную форму нормального сечения 142434определяют способом замены плоскостей проекций.
Чтобы построить развертку призмы, нормальное сечение 142434“разворачиваем” в прямую линию нормального сечения 1231и через каждую точку проводим перпенди-куляры к этой прямой (рис. 13.2, б). На каждом из построенных перпендикуляров от-кладываем по обе стороны от линии нормального сечения отрезки боковых ребер, из-меренные на плоскости П2до нормального сечения и после него. Например, отрезки A-1и 1-A′на развертке равны отрезкам A212и 12A′2на фронтальной проекции призмы. Точно так же B-2=B222, B′-2=B′222и C-3=C232, C′-3=C′232. Соединяя точки А,В,Си А′, В′, С′, получаем развертку боковой поверхности призмы.
Присоединяя к развертке боковой поверхности призмы оба основания (треугольни-ки АВСи А′В′С′), получаем полную развертку призмы (см. рис. 13.2, б
Хотя все остальные поверхности (не относящиеся к многогранным, цилиндриче-ским, коническим, торсовым) теоретически не развертываются на плоскость, инженер-ная практика, тем не менее, требует построения их “разверток”. Для неразвертываю-щихся поверхностей строят так называемые условные развертки.
13.1. Построение разверток поверхностей многогранников
Напомним, что многогранником называют пространственную геометрическую фи-гуру, со всех сторон ограниченную плоскими многоугольниками (гранями). Развертка многогранника представляет собой плоскую фигуру, которая получается при совмеще-нии граней многогранника с плоскостью. Процесс построения развертки поверхности многогранника сводится к построению истинных величин его граней, что непосредст-венно связано с определением натуральной (истинной) длины каждого ребра много-гранника. Рассмотрим построение разверток наиболее распространенных многогран-ных поверхностей – поверхностей пирамид и призм.
13.1.1. Развертка пирамиды
Поверхность n-угольной пирамиды включает в себя основание (плоский n-угольник) и боковую поверхность, состоящую из nтреугольников. Для построения раз-вертки пирамиды необходимо определить натуральные величины боковых ребер и сто-рон основания. На рис. 13.1, аизображена треугольная пирамида ABCS. Основанием
пирамиды является треугольник АВС, расположенный в плоскости,
параллельной гори-зонтальной плоскости проекций, поэтому стороны основания AB, BC, AC проецируются на П1в натуральную величину.
Длины боковых ребер пирамиды определяются с помощью вспомогательных пря-моугольных треугольников. Вспомогательные треугольники имеют общий катет S2O0(разность высот концов боковых ребер пирамиды). Другой катет равен длине горизон-тальной проекции соответствующего ребра. Например, в треугольнике S2O0A0катет S2O0равен разности высот точек Sи А. Другой катет O0А0равен горизонтальной проек-ции ребра SA: O0A0=S1A1. Истинная длина ребра SAравна величине гипотенузы S2A0. Аналогично длина ребра SB равна S2B0, а длина ребра SC равна S2C0.
 S2
S2 K2 K0 A A 1
K2 K0 A A 1A2 B
B2 12 C2 O0
A1 11 C1K1
C0B010 A0 K
A C
B1
S1
а)
Рис. 13.1
SK=S2K0
б) S
Развертка боковой поверхности пирамиды состоит из трех примыкающих друг к другу треугольников (рис. 13.1, б), конгруэнтных соответствующим граням пирамиды. Например, треугольник ACS(развертка соответствующей грани пирамиды) построен по известной длине стороны ACи найденным на рис. 13.1, адлинам боковых ребер пира-миды AS и CS. К развертке боковых граней пирамиды пристраиваем ее основание ABC.
Пусть на поверхности пирамиды отмечена точка K. Чтобы найти положение этой точки на развертке, проводим через Kвспомогательную прямую S-K-1, отмечаем на развертке точку 1и с помощью прямоугольного треугольника S2O010находим истин-ную длину отрезка SK=S2K0. Откладывая этот отрезок на развертке от точки Sвдоль прямой S-1, находим точку K.
13.1.2. Развертка призмы
На рис. 13.2, аизображена наклонная призма. Призма расположена таким образом, что ее основание параллельно горизонтальной плоскости проекций, поэтому на П1ос-нование ABCпризмы проецируется в натуральную величину A1B1C1. Боковые ребра призмы параллельны фронтальной плоскости проекций, поэтому на П2они проециру-ются без искажения.
Развертка боковой поверхности призмы может быть получена способомнормально-госечения.Для этого боковую поверхность призмы рассекают фронтально-
проецирующей плоскостью Σ, перпендикулярной боковым ребрам призмы. Истинную форму нормального сечения 142434определяют способом замены плоскостей проекций.
Чтобы построить развертку призмы, нормальное сечение 142434“разворачиваем” в прямую линию нормального сечения 1231и через каждую точку проводим перпенди-куляры к этой прямой (рис. 13.2, б). На каждом из построенных перпендикуляров от-кладываем по обе стороны от линии нормального сечения отрезки боковых ребер, из-меренные на плоскости П2до нормального сечения и после него. Например, отрезки A-1и 1-A′на развертке равны отрезкам A212и 12A′2на фронтальной проекции призмы. Точно так же B-2=B222, B′-2=B′222и C-3=C232, C′-3=C′232. Соединяя точки А,В,Си А′, В′, С′, получаем развертку боковой поверхности призмы.
Присоединяя к развертке боковой поверхности призмы оба основания (треугольни-ки АВСи А′В′С′), получаем полную развертку призмы (см. рис. 13.2, б