ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 86
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Определение. Триангуляция–замена(аппроксимация)даннойповерхностимного-гранной поверхностью, состоящей из треугольныхграней.
После аппроксимации поверхности конуса поверхностью вписанной в него пира-миды надо построить точную развертку пирамиды. Размеры всех боковых ребер пира-миды равны между собой и равны длине l очерковой образующей конуса.
 l
l2212
A2
S2
 4252
425232 B2
A
S
l
1 2345B
A1
11
S1 B1

 51213141
51213141а) б) Рис. 13.6
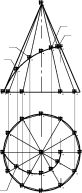
Чтобы построить развертку пирамиды, на свободном месте чертежа произвольно выбираем положение вершины развертки – точку S, и строим 12 одинаковых треуголь-ников с общей вершиной S. Боковые стороны каждого треугольника равны длине l очерковой образующей конуса. Основание каждого треугольника равно длине стороны правильного многоугольника, вписанного в круговое основание конуса. Получаем раз-вертку вписанной в конус пирамиды в виде 12 треугольников со смежными сторонами. Построенная таким образом точная развертка пирамиды принимается за приближен-ную развертку боковой поверхности конуса. Основание пирамиды (правильный 12-угольник) принимается за развертку основания конуса (рис. 13.6, б).
Отметим на поверхности конуса две точки Aи B (см. рис. 13.6, а). Кратчайший путь между двумя точками, проложенный по данной поверхности, называют геодезической линией.
Задача. Наповерхностиконусапостроитькратчайшийпуть(геодезическуюли-нию)между точками A и B (см. рис. 13.6, а).
Построение геодезической линии ABна поверхности выполняется с помощью раз-вертки. Прямой линии на развертке соответствует кратчайший путь на поверхности (почему?). Переносим точки A, Bс чертежа конуса на развертку и соединяем Aи Bот-резком прямой (см. рис. 13.6, б). Затем на отрезке ABотмечаем промежуточные точки 1, 2,…5 и “возвращаем” эти точки на чертеж конуса.
Соединяя плавной кривой фронтальные проекции точек A, 1, 2, 3, 4, 5, B, получаем фронтальную проекцию геодезической линии AB. Соединяя плавной кривой горизон-
тальные проекции точек A, 1, 2, 3, 4, 5, B, получаем горизонтальную проекцию геодези-ческой линии AB. Задача решена приближенно, так как для решения использована при-ближенная развертка конической поверхности.
13.2.4. Приближеннаяразвертка поверхности наклонного конуса
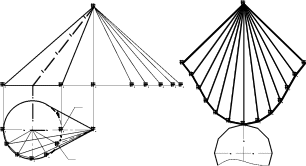
На рис. 13.7 построена приближенная развертка поверхности наклонного конуса с круговым основанием. Для построения приближенной развертки поверхность конуса заменена поверхностью вписанной в него двенадцатиугольной пирамиды.
 S2 S
S2 SΔz B′ B
A2 B2 S0 5 50403020104
B1 3
A1 S1 A 12
11
21 31 41
51
Рис. 13.7
Поверхность конуса имеет плоскость симметрии, поэтому развертка представляет собой симметричную фигуру. В плоскости симметрии лежит самая короткая образую-щая SВ, по которой сделан разрез поверхности. Самая длинная образующая SА, также лежащая в плоскости симметрии, является осью симметрии развертки поверхности.
Натуральные величины образующих определены способом вспомогательного пря-моугольного треугольника. Например, истинная длина образующей S-1найдена как ги-потенуза S210прямоугольного треугольника S2S010. Один катет этого треугольника – разность высот Δzконцов образующей (эта величина одинакова для всех образующих конуса). Другой катет S010равен длине S111горизонтальной проекции образующей.
От оси симметрии SАстроим примыкающие друг к другу треугольники – шесть треугольников в одну сторону и шесть в другую. Все треугольники имеют общую вер-шину S. Каждый из треугольников строится по трем сторонам. Боковые стороны каж-дого треугольника равны истинным величинам ребер вписанной в конус пирамиды, а основание треугольника равно длине стороны многоугольника, вписанного в круговое основание конуса.
13.2.5. Приближенная развертка поверхности усеченного конуса
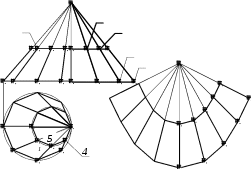
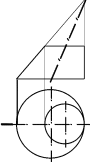
Дан усеченный конус с круговым основанием, наклонной осью и плоскостью сим-метрии Ф||П2(рис. 13.8, а). Вписываем в конус 8-угольную усеченную пирамиду, вер-шина которой совпадает с вершиной Sусеченного конуса (рис. 13.8, б). Точную раз-вертку поверхности вписанной усеченной пирамиды будем считать приближенной раз-верткой усеченного конуса.
Размеры боковых ребер пирамиды от вершины Sдо основания определены спосо-бом вспомогательного прямоугольного треугольника (см. рис. 13.8, б). Например, дли-на ребра S-1найдена как гипотенуза S210прямоугольного треугольника S2B210. Катет S2B2этого треугольника – разность высот концов ребер, одинаковая для всех ребер пи-рамиды. Другой катет B210равен длине S111горизонтальной проекции ребра S-1.
 S2 S2
S2 S240
62 50
D2 5242 C2 60
A2 22
12 32 B2 30
Ф1 A1 D1 B1=C1=S1116 1311
21
20
10
S
C
4
5 B
D 6 3
2
A 1
а) б) в)
Рис. 13.8
Считая, что пирамида не усечена, построим ее развертку. Развертка каждой грани представляет собой треугольник, боковые стороны которого равны длинам соответст-вующих ребер неусеченной пирамиды (они определены на рис. 13.8, б), а длина осно-вания равна длине стороны 8-угольника, вписанного в круговое основание конуса. Раз-вертка поверхности неусеченной пирамиды представляет собой 8 примыкающих друг к другу треугольников с общей вершиной S (рис. 13.8, в).
Пирамида усечена плоскостью, параллельной ее основанию, поэтому истинная фор-ма каждой грани усеченной пирамиды – трапеция. Развертка поверхности усеченной пирамиды представляет собой примыкающие друг к другу трапеции. Отложим на раз-вертке неусеченной пирамиды истинную длину какого-нибудь ребра усеченной пира-миды (например, длину ребра BC, изображенного на П2в натуральную величину). Че-рез точку Cна развертке проводим отрезок C-4, параллельный отрезку B-3. Затем из точки 4проводим отрезок 4-5, параллельный отрезку 3-2. Продолжая построение, по-лучаем развертку усеченной пирами
ды в виде набора из восьми примыкающих друг к другу трапеций (см. рис. 13.8, в).
Развертки нижнего и верхнего оснований усеченной пирамиды (не показанные на чертеже), имеют форму правильных 8-угольников, вписанных в нижнее и верхнее кру-говые основания данного усеченного конуса.
13.2.6. Приближенная развертка поверхности наклонного цилиндра
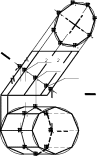
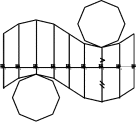
Дан наклонный цилиндр с круговым основанием (рис. 13.9, а). Вписываем в ци-линдр 8-угольную наклонную призму (рис. 13.9, б). Точную развертку поверхности призмы будем считать приближенной разверткой поверхности наклонного цилиндра.
 Г2 A′2
Г2 A′272
64
74
84
14 24
6=8
12=5222=42
54
44
 34
34A′
A2 32 Г 1 2 351
4 5 6 178
A1 71 61 41 31 A
81 21
11
а) б) в)
Рис. 13.9
Развертку боковой поверхности призмы получают способом нормального сечения, в соответствии с которым боковую поверхность призмы рассекают фронтально-проецирующей плоскостью Г, перпендикулярной ее боковым ребрам (см. п. 13.1.2). Ис-тинная форма нормального сечения призмы 1424…84определена способом замены плоскостей проекций. Нормальное сечение 1424…84“разворачиваем” в прямую 1-2-…-8-1и через каждую точку проводим прямую, перпендикулярную линии нормального сечения (рис. 13.9, в). На каждом из построенных перпендикуляров откладываем отрез-ки боковых ребер, измеренные на П2до и после нормального сечения. Например, от-резки A-7и A′-7на развертке равны отрезкам A272и A′272на плоскости П2. Концы от-резков соединяем ломаными линиями. К развертке боковой поверхности призмы до-бавляем ее основания – два многоугольника (см. рис. 13.9, в).
13.3. Построение условных разверток неразвертывающихся поверхностей
Многие сооружения часто ограничены неразвертывающимися поверхностями. Ме-жду тем условия их постройки заставляют изготавливать эти поверхности из листового материала. Поэтому составление условных разверток неразвертывающихся поверхно-стей представляет собой важную техническую задачу. Например, поверхность корпуса морского судна составляется из отсеков криволинейных поверхностей, которые вы-краивают из металлических листов, а затем склепывают друг с другом. Образуется кри-вая (а в сущности – многогранная) поверхность корпуса.
Пусть требуется построить условную развертку некоторой неразвертывающейся поверхности Ф. Разбиваем поверхность Фна отдельные участки (отсеки). Каждый от-сек аппроксимируем (приближенно заменяем) отсеком какой-либо развертывающейся поверхности – многогранником, цилиндром или конусом (в зависимости от формы дан-