Файл: Умноженной на множитель в форме показательной функции W.docx

4. (материал из методички) По карте нулей и полюсов можно определить местоположение максимумов, минимумов и нулей АЧХ в основной полосе частот [0; π], а именно:

• 
  частота комплексно сопряженного полюса _*k, где _*k = 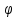_*k в (34), соответствует частоте максимума АЧХ (приблизительно);
  
• 
  частота комплексно сопряженного нуля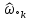 , где 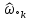= 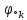(34), соответствует частоте минимума АЧХ (приблизительно), если 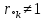, или нуля АЧХ, если 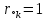(комплексно сопряженные нули на единичной окружности); в точке нуля АЧХ наблюдается скачок ФЧХ на π;
  
• 
  вещественным нулям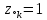 и/или 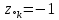(на единичной окружности) соответствует нуль АЧХ на границе основной полосы частот 0 и/или π.
  

Формула 34

Комплексно сопряженные нули 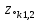и полюсы 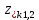представляют в показательной форме, где аргументы – углы (в радианах) на комплексной z – плоскости: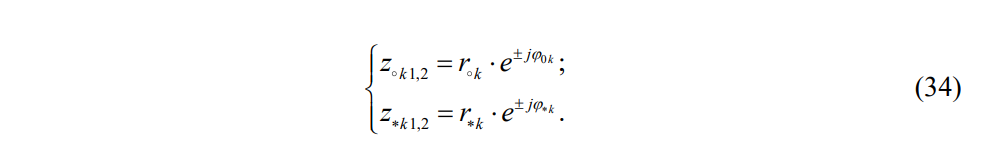

10. Представление аналоговых сигналов в частотной области: спектр периодических сигналов и спектральная плотность апериодических сигналов. Их связь, физический смысл и размерность. Свойства интегрального преобразования Фурье (линейность, сдвиг во временной области, сдвиг в частотной области, преобразование произведения сигналов, преобразование свертки сигналов).

Во временной области:

• 
  Сигналы (аналоговые и дискретные) описываются функциями времени;
  
• 
  Линейные системы (аналоговые и дискретные) описываются:
  

---

* Характеристиками. Характеристика линейной системы определяется как ее реакция на некоторый тестовый сигнал, т. е. характеристика — это сигнал, описываемый функцией времени;

* Соотношением вход/выход. Соотношение вход/выход линейной системы описывается линейным уравнением, устанавливающим связь между входным и выходным сигналами - функциями времени. По умолчанию будем считать, что системы имеют одни вход и один выход.
Тип функции времени определяется типом сигнала, а именно:

• 
  Непрерывная функция х(t) описывает аналоговый сигнал;
  
• 
  Последовательность (решетчатая функция) х(nT) описывает дискретный сигнал.
  

Помимо временной, сигналы и линейные системы могут описываться и в других областях (в областях иных независимых переменных), при этом соответствующие функции времени преобразуются в функции другой переменной.
Математическое описание аналоговых сигналов и линейных систем в р-области (на комплексной р-плоскости) и в частотной области основано соответственно на преобразованиях Лапласа и Фурье функции времени, для которой выполняется условие



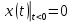
Представление аналоговых сигналов в частотной области: спектр периодических сигналов и спектральная плотность апериодических сигналов.
О СПЕКТРЕ

Формула ряда Фурье, переписанная в вид:

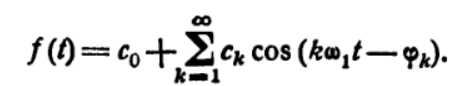, где основная частота.
Сложная периодическая функция определяется совокупностью c_k и φ_k. Совокупность величин c_k носит название спектра амплитуд. Совокупность величин φ_k называется спектром фаз.
Спектр периодической функции можно изобразить графически. Выберем для этого координаты c_k и ω = kω₁. Спектр будет изображён в этой системе совокупностью дискретных точек, т.к. каждому значению

---

kω₁ соответствует определённое c_k. График, состоящий из отдельных точек неудобен, поэтому принято изображать амплитуды отдельных гармоник вертикальными отрезками соответствующей длины. В результате спектр периодической функции принимает вид:

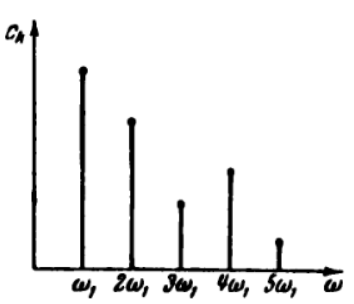(рис. 1)

Это дискретный спектр, его так же называют линейчатым. Второе свойство спектра (рис. 1) состоит в том, что спектр гармонический. Т.е. состоит из равноотстоящих спектральных линий; частоты гармоник находятся в простых кратных соотношениях. Отдельные гармоники могут отсутствовать (амплитуда равна нулю), но это не нарушает гармоничности спектра.



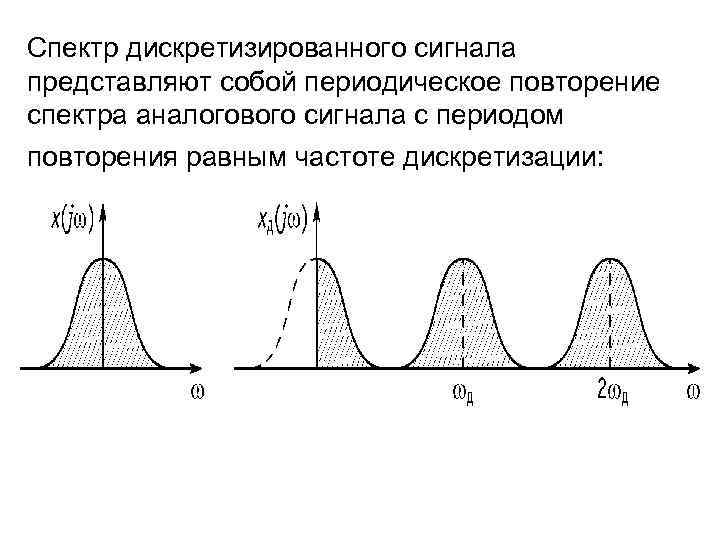
(КАРТИНКА С ИНЕТА)

О СПЕКТРАЛЬНОЙ ПЛОТНОСТИ

Обращаясь к спектрам непереодических функций. Как известно, в результате предельного перехода от ряда к интегралу Фурье интервалы между отдельными спектральными линиями неограниченно сокращаются, линии сливаются, и вместо дискретных точек спектр должен изображаться непрерывной последовательностью точек, т.е. непрерывной кривой. Такого рода спектр называется сплошным.

Следует ввести уточнение. Ранее была записана формула интеграла Фурье в виде:


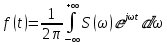
Подинтегральная функция выражает отдельное, бесконечно малое слагаемое, т.е. колебание с бесконечно малой амплитудой dC:

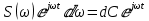
Отсюда находим:


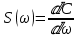
Таким образом величина S(ω) выражает не непосредственно амплитуду, а спектральную плотность. Однако обычно эту деталь опускают и называют S(ω) комплексным спектром непериодической функции, а абсолютное значение (модуль) этой величины просто спектром.



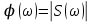
Их связь, физический смысл и размерность.

(Инфа не найдена)
Свойства интегрального преобразования Фурье (линейность, сдвиг во временной области, сдвиг в частотной области, преобразование произведения сигналов, преобразование свертки сигналов).

---

(Тут всё с инета, т.к. в книгах инфы не найдено)
Свойство линейности

Пусть даны непериодические сигналы a(t) и b(t), а также их спектральные плотностиA(ω) и B(ω) соответственно. Везде далее мы будем предполагать, что a(t) и b(t) — абсолютно интегрируемые сигналы, тогда преобразование Фурье сигнала s(t) = a(t) + b(t) равно



Следствием является свойство умножения на константу  :



Свойство временного сдвига

Рассмотрим сигнал s(t) = a(t – τ) как результат временного сдвига исходного сигнала a(t) на произвольную величину τ. Тогда преобразование Фурье сигнала s(t) имеет вид:

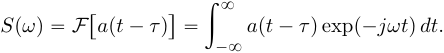(3)

Введем замену переменной ξ = t - τ, тогда t = ξ + τ и dt = dτ. При любом конечном τ пределы интегрирования не меняются и спектральная плотность s(ω) равна:

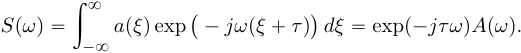(4)

Таким образом, задержка сигнала во времени приводит к изменению фазы его спектральной плотности без изменения амплитуды.
Сдвиг в частотной области

Сдвиг аргумента спектральной плотности X(f) по частоте на f₀ эквивалентен

умножению во временной области на множитель .



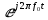Доказательство:

.

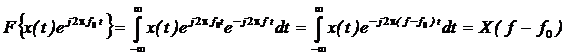Умножение комплексной экспоненты 

---

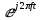
с частотой f₀ на функцию x(t) математически означает амплитудную модуляцию (АМ) комплексной экспоненты (комплексной несущей) низкочастотным сигналом x(t).
Разновидности АМ с гармонической несущей

 - сигнал с косинусоидальной несущей,

 - сигнал с синусоидальной несущей.

.

В АМ радиовещании (длинные и средние волны) амплитудно – модулированный сигнал имеет вид   , где константа m – это индекс модуляции.

В соответствии со свойством модуляции      , т.е. при модуляции спектр X(f) сигнала x(t) сдвигается в частотной области на частоту несущей.

Представив по формуле Эйлера   , получим , т.е. при модуляции косинусоидальной несущей спектр исходного сигнала x(t) сдвигается в частотной области влево и вправо на f₀.  

Т.о., при АМ происходит перенос низкочастотного спектра сигнала на частоту модуляции f_0.

Преобразование Фурье произведения сигналов

Пусть сигнал s(t) = a(t)b(t) представляет собой произведение сигналов a(t) и b(t). Преобразование Фурье сигнала s(t) равно:

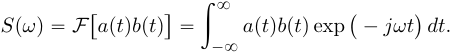(8)
Подставим в (8) вместо сигнала a(t) обратное преобразование Фурье его спектральной плотности A(ω):

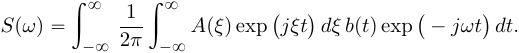(9)

Поменяем в (9) операции интегрирования и получим:

---