Файл: Умноженной на множитель в форме показательной функции W.docx

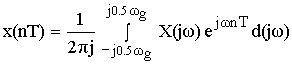
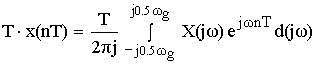
Устремляем T к нулю. Если  , то T вырождается в непрерывную переменную 

Денормированные формулы прямого и обратного преобразования Фурье для непрерывных сигналов:



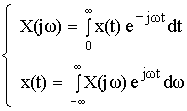
Это доказывает справедливость формулы Фурье для дискретного сигнала. Переменную ω можно распространить на всю плоскость комплексного переменного:  , и тогда формулы Фурье для дискретного сигнала заменяются формулами Лапласа.

 – прямое преобразование.

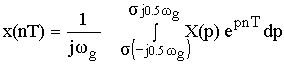 – обратное преобразование.

Интервал/период дискретизации, частота и угловая частота дискретизации.

При выборе периода дискретизации можно воспользоваться теоремой В.А.Котельникова, согласно которой всякий непре­рывный сигнал, имеющий ограниченный частотный спектр, пол­ностью определяется своими дискретными значениями в моменты отсчета, отстоящие друг от друга на интервалы времени:

Т_д = 1/2F_max ,

где F_max – максимальная частота в частотном спектре сигнала.



УГЛОВАЯ ЧАСТОТА ДИСКРЕТИЗАЦИИ, BITCH WHAT???

бля это реально все (т – период дискретизации вродь)

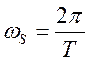(рад/сек), еще можно записать как омега=2пи*Ф (Ф – частота) 

4. Связь прямого Z-преобразования с дискретным преобразованием Лапласа. Отображение P-плоскости в Z-плоскость. Преобразование начала координат, оси частот, левой и правой полуплоскостей из P-плоскости в Z-плоскость. Неоднозначность преобразования P-плоскости в Z-плоскость (наложение множества точек на прямой из P-плоскости в одну точку Z-плоскости).

---

Связь прямого Z-преобразования с дискретным преобразованием Лапласа.

Связь Z-преобразования с преобразованием Лапласа найдем, записав аналоговый сигнал в виде суммы дискретных отсчетов и набора дельта-функций:

 (9.13)

где  шаг дискретизации. Преобразование Лапласа для такого сигнала равно:

 (9.14)

Воспользовавшись фильтрующим свойством дельта-функции, получим:

 (9.15)

Сравнивая соотношения (9.1) и (9.15), замечаем, что одна формула переходит в другую при замене  . Таким образом, Z-преобразование можно получить из преобразования Лапласа путем перехода к новой переменной:

 (9.16)

Смысл использования Z-преобразования при анализе дискретных сигналов вытекает из следующего. Так как справедливо соотношение:

 , (9.17)

то изменение фазовой характеристики сигнала   означает задержку сигнала на один шаг дискретизации   и соответствует задержке сигнала на один такт в  области.

Переход от преобразования Лапласа к Z-преобразованию при описании дискретных систем необходим по следующей причине. Дискретизация аналогового сигнала приводит к периодичности частотного спектра, то есть появлению бесконечного ряда сдвинутых копий спектра исходного непрерывного сигнала. Очевидно, эффект дискретизации приводит к появлению в плоскости 

---

 бесконечной конфигурации особых точек (полюсов и нулей), повторяющихся через интервал  .

При переходе от  плоскости к  плоскости точка   отображается в точку  . Поэтому путь вдоль мнимой оси   в  плоскости отображается в единичную окружность в  плоскости, так как на мнимой оси   и, следовательно   Можно показать, что левая (устойчивая) полоса  плоскости шириной   отображается внутрь круга единичного радиуса  плоскости. Все последующие полосы  плоскости шириной  , соответствующие периодическому частотному спектру дискретного сигнала, также отображаются внутрь круга единичного радиуса  плоскости. Поэтому конфигурация особых точек (полюсов и нулей) в  плоскости становится конечной.

Отображение

---

P-плоскости в Z-плоскость.

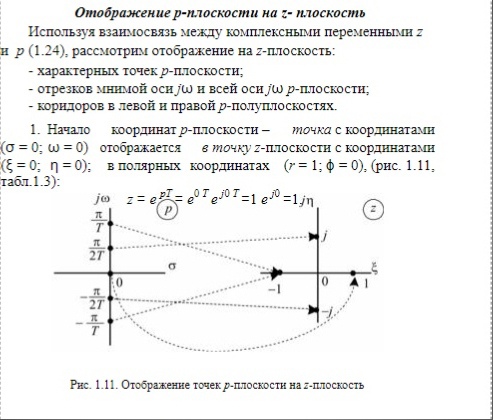
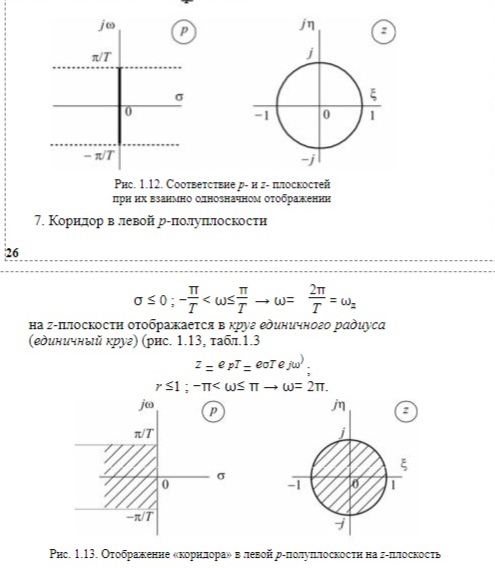
Преобразование начала координат, оси частот, левой и правой полуплоскостей из P-плоскости в Z-плоскость. (ВОТ ЭТО ХЗ)

Отображение p-плоскости на z-плоскость

p-плоскость p = s + jw				z-плоскость z = x + jh = rejj
№	s	w		x	h	r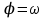
1	0	0		1	0	1	0
2	– 	0		0	0	0	0
3	0		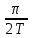	0	1	1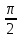
4	0		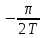	0	– 1	1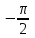
5	0		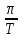	– 1	0	1	p
6	0		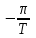	– 1	0	1	–p
7	Отрезок мнимой оси			Единичная окружность (один оборот)
	0		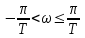	r = 1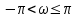
8	Коридор в левой p-полуплоскости			Единичный круг
	s ≤ 0		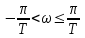	r ≤ 1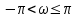
9	Коридор в правой p-полуплоскости			Область вне единичного круга
	s > 0		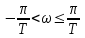	r > 1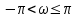

---

5.   1   2   3   4   5   6   7   8

---