Файл: Умноженной на множитель в форме показательной функции W.docx

Обратное Z-преобразование. Вычисление обратного z-преобразования с помощью вычетов. Формулы для вычисления вычетов в простых и кратных полюсах. Пример вычисления обратного z-преобразования.

Z- преобразование является обобщением дискретного преобразования Фурье.

В общем случае, z-преобразование – это степенной ряд с бесконечным количеством членов, поэтому он может сходиться не для всего пространства значений z. Область z, в которой z-преобразование сходится и значения S(z) конечны, называют областью сходимости.

Значения z, для которых S(z)=∞, называются полюсами, а для которых S(z)=0, называются нулями функции S(z). Как видно из примеров, для последовательностей конечной длины z-преобразование сходится везде, кроме точки z=∞, для имеющих правостороннюю часть (k≥0) и точки z=0 для имеющих левостороннюю часть (k<0), в любых их комбинациях. Для бесконечных причинных последовательностей преобразование сходится везде внутри круга единичного радиуса с центром в начале координат.

По заданному или полученному в результате анализа какой-либо системы z-полиному однозначно восстанавливается соответствующая этому полиному функция путем идентификации коэффициентов степеней при zk с k-отсчетами функции.

Обратное преобразование методы:

Обратное z-преобразование позволяет восстанавливать дискретную функцию по ее z-образу. Оно широко используется, например, при определении импульсных характеристик рекурсивных цифровых фильтров. В символической форме:



На практике X(z) в процессе расчетов обычно выражается через отношение двух многочленов от z:



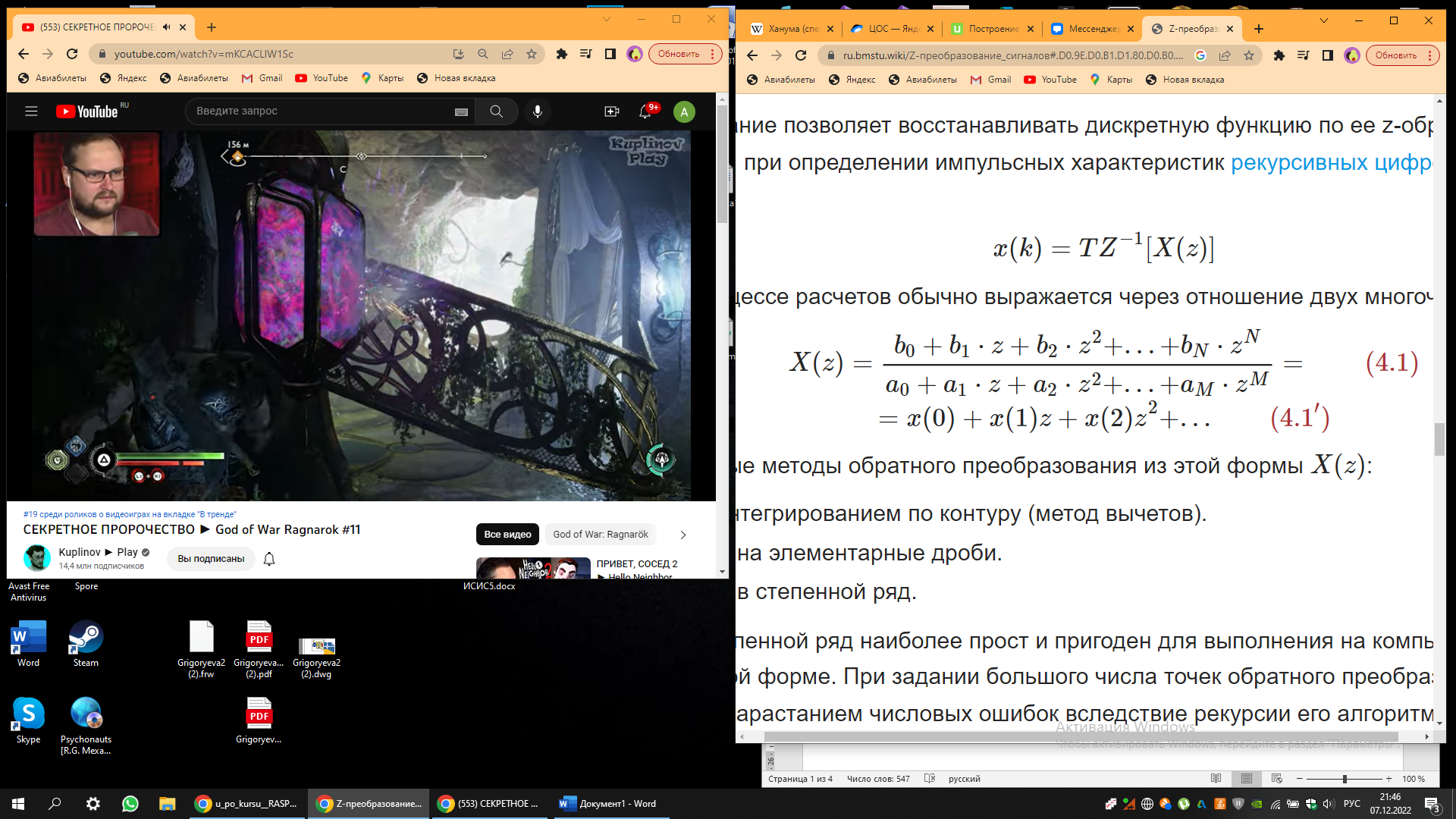
Самые распространенные методы обратного преобразования из этой формы X(z):

• 
  Преобразование интегрированием по контуру (метод вычетов).
  
• 
  Метод разложения на элементарные дроби.
  
• 
  Метод разложения в степенной ряд.
  

---

Метод разложения в степенной ряд наиболее прост и пригоден для выполнения на компьютерах, но он не дает решения в аналитической форме. При задании большого числа точек обратного преобразования требуется также следить за возможным нарастанием числовых ошибок вследствие рекурсии его алгоритма.

Два первых метода позволяют получать результаты в аналитическом виде, но требуют вычисления полюсов функции X(z), что может представлять трудности при высоком порядке функции. При высоких порядках полюсов потребуется также дифференцирование соответствующих порядков.
(Формулы для вычисления вычетов в простых и кратных полюсах)

Согласно этой теореме контурный интеграл равен сумме вычетов подынтегральной функции в полюсах z_v, v=l,2,...,N, расположенных в области, охватываемой окружностью радиуса р :



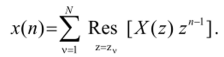
Для простого полюса z_v вычет вычисляется по формуле   а для полюса порядка т - по формуле 
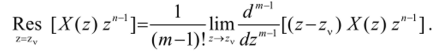
(ОЧЕНЬ ДУШНОЕ РЕШЕНИЕ, ЗАРАНЕЕ ОТКРОЙТЕ ОКНО)

Формально обратное -преобразование  функции  определяется соотношением



Где интеграл в выражении представляет собой контурный интеграл по замкнутому пути С.

Метод вычетов. Если является рациональной функцией переменной, то выражение (11.54) можно оценить с помощью теоремы о вычетах, которая устанавливает, что



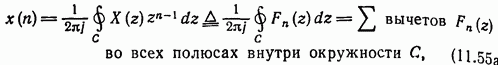
где



Пример 11.8. Определить с помощью метода вычетов обратное -преобразование 

---

Решение. Предположим, что



Тогда уравнение (11.55) показывает, что последовательность образуется суммой вычетов во всех полюсах внутри некоторой окружности С.



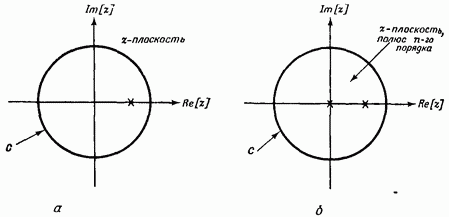
Рис. 11.6. Расположение полюсов функции в выражении (1157). а — для — для Обозначения X — расположения полосов.

Для простоты выберем окружность С с радиусом большим в-плоскости. При замкнутый путь С охватывает только один полюс в точке как показано на рис. 11.6, а. Следовательно, из уравнения (11.55 а) получаем при



Для функцию можно переписать в виде



Это означает, что имеется простой полюс в точк и полюс в точке с кратностью как показано на рис. 11.6, б. Следовательно,



гд — соответственно вычеты в точках

Пр получаем



Следовательно,



При получаем



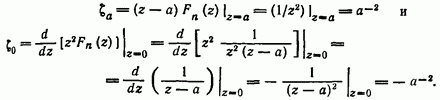
Следовательно,



Это приводит к тому, что для каждого получаем

Из соотношений (11.58) и (11.64) обратное-преобразование функции заданной выражением (11.56), имеет вид



(СМЫСЛ ЭТОГО МЕТОДА\НАХУЯ\ЧЕМ КРУТ, КОГДА СОВСЕМ ПИЗДЕЦ ПО ОТВЕТУ МОЖНО НАВАЛИТЬ ВОДЫ)

Методы разложения на элементарные дроби и вычетов дают результаты в аналитическом виде. Главный их недостаток – необходимость разложения на множители многочлена знаменателя

---

, т.е. находить полюсы функции X(z). Если порядок функции высокий, то поиск полюсов X(z), если функция не представлена в разложенном виде, – задача довольно трудная. Кроме того, если функция X(z) имеет полюсы высокого порядка, то оба метода могут потребовать включения операции дифференцирования высокого порядка. Однако, если нужно найти решение в аналитическом виде, то лучше выбрать метод вычетов или разложения на элементарные дроби. Последний метод особенно полезен для генерирования коэффициентов параллельных структур для цифровых фильтров. Метод вычетов также нашел широкое применение при анализе ошибок квантования в системах дискретного времени.

Ниже как раз и есть обратное z преобразование

6. 1   2   3   4   5   6   7   8

---

Разностные уравнения. Решение разностных уравнений с помощью Z-преобразования. Пример решения разностных уравнений с помощью Z-преобразования.

Разностные уравнения – это алгоритм функционирования дискретной цепи. Разностное уравнение записывается непосредственно по схеме



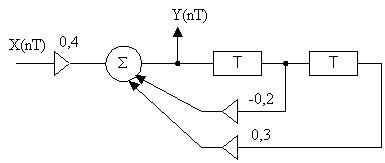
Структурная схему по следующему разностному уравне­нию:

Y(nT) = 0,4Х(пТ) - 0,2Y(nT - Т) + 0,3Y(nT - 2Т)



Пример:

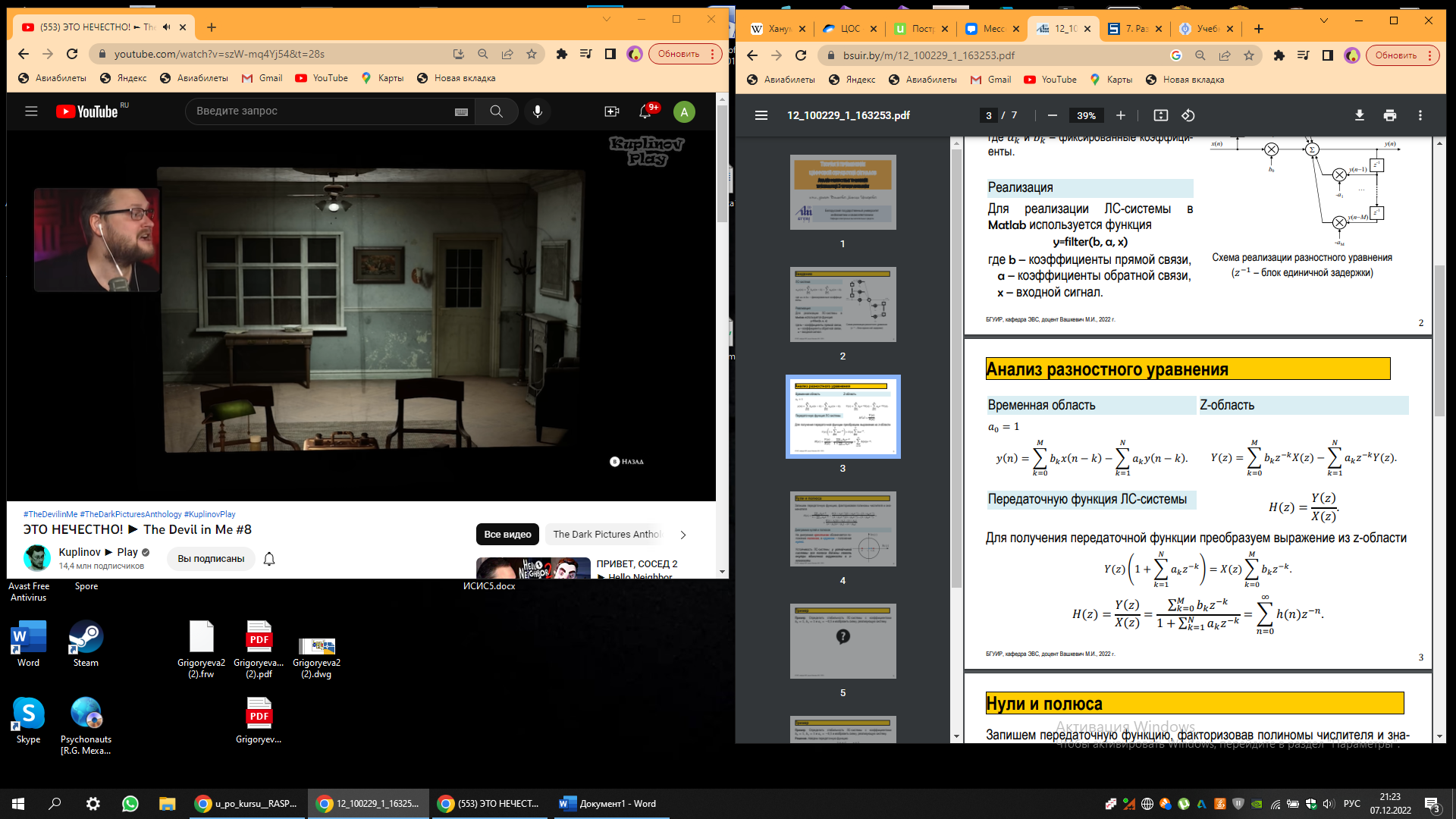
Составить разностное уравнение по заданной структурной схеме (рис.5) и решить его для заданной последовательности Х(пТ)={1,0; 0,5;0}


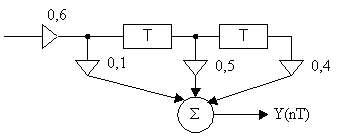
Рисунок 5.

Решение: Данной структурной схеме соответствует разностное урав­нение

Y(nT) = 0,6[0,1Х(nТ) + 0.5Х(nТ - Т) + 0,4Х(nТ - 2Т)]

n = 0 → Y(OT) = 0,6*0,1Х(0Т) = 0,06

n = 1 → Y(1T) = 0,6[0,1Х(1Т) + 0,5Х(1Т - Т)]= 0,6*0,1*0,5 + 0,6*0,5*1=0,45

n = 2 → Y(2T) = 0,6[0,1Х(2Т) + 0,5Х(2Т - Т) + 0,4Х(2Т - 2Т)] =

= 0,6[0,1*0 + 0,5*0,5 + 0,4*1] = 0,39

Y(nT)= {0,06; 0,45; 0,39}

Наряду с разностным уравнением очень часто структуру цифрового фильтра характеризуют передаточной характеристикой. Если разностное уравнение характеризует заданную цепь во временной области, то переда-

точная характеристика характеризует эту же цепь в частотной области. Численное выражение для передаточной характеристики равно:

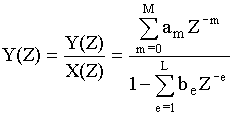                                                   (3)

В выражении (3) Y(Z) – Z - преобразование выходного сигнала.

X(Z) – Z - преобразование входного сигнала. Z = е ^-j2π/N: Т - период дискретизации, w - круговая частота, a_m - коэффициенты передачи нерекурсивной цепи, b_e - коэффициенты передачи рекурсивной цепи, Z^-1 - характеризует задержку сигнала не один тактовый интервал, М, L - соответственно характеризует количество прямых и обратных связей системы.

Если 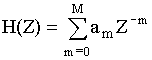 , то цепь называется нерекурсивной.

Если 

---