• 
  работа в среде типовых математических моделей, включая решение основных задач моделирования типа "как сделать, чтобы?", "что будет, если?", анализ чувствительности и др.;
  
• 
  быстрая и адекватная интерпретация результатов моделирования;
  
• 
  оперативная подготовка и корректировка входных параметров и ограничений модели;
  
• 
  графическое отображение динамики модели;
  
• 
  объяснение пользователю необходимых шагов формирования и работы модели.
  

Экспертные ИС (Expert Systems – ES) обеспечивают выработку и оценку возможных альтернатив пользователем за счет создания ИС, связанных с обработкой знаний. Экспертные системы основаны на использовании искусственного интеллекта, и дают возможность менеджеру или специалисту получать консультации экспертов по любым проблемам, о которых этими системами накоплены знания.

Экспертные системы подразделяются:

• 
  по степени централизации обработки – на информационно-централизованные, децентрализованные, информационной системы коллективные использования
  
• 
  по степени интеграции функций — многоуровневые ИС с интеграцией по уровням управления (цеха – производство, управления – предприятие, предприятие – объединение, объединение — корпорация и т.д.), многоуровневые с интеграцией по уровням планирования и т.п.
  

Экспертные информационные системы обеспечивают выработку и оценку возможных альтернатив пользователем за счет создания экспертных систем, связанных с обработкой знаний. Архитектура экспертной системы включает в себя два основных компонента: базу знаний (хранилище единиц знаний) и программный инструмент доступа и обработки знаний, состоящий из механизмов, выводов, заключений (решения), для приобретения знаний, объяснения получаемых результатов и интеллектуального интерфейса. Причем центральным компонентом экспертной системы является база знаний, которая выступает по отношению к другим компонентам как содержательная подсистема, составляющая основную ценность.

База знаний это совокупность единиц знаний, которые представляют собой формализованное с помощью некоторого метода представления знаний отражение объектов проблемной области и их взаимосвязей, действий над объектами и, возможно, неопределенностей, с которыми эти действия осуществляются.

---

Экспертная поддержка принимаемых пользователем решений реализуется на двух уровнях.

Работа первого уровня экспертной поддержки исходит из концепции «типовых управленческих решений», в соответствии с которой часто возникающие в процессе управления проблемные ситуации можно свести к некоторым однородным классам управленческих решений, т.е. к некоторому типовому набору альтернатив. Для реализации экспертной поддержки на этом уровне создается информационный фонд хранения и анализа типовых альтернатив.

Если возникшая проблемная ситуация не ассоциируется с имеющимися классами типовых альтернатив, в работу должен вступать второй уровень экспертной поддержки управленческих решений. Этот уровень генерирует альтернативы на базе имеющихся в информационном фонде данных правил преобразования и процедур оценки синтезированных альтернатив.

Сравнительный анализ существующих систем
На сегодняшний день во многих сферах деятельности для решения задач аналитического планирования широко используется метод анализа иерархий, созданный американским ученым Т. Саати. Для объективной оценки ИС среди аналогов будет использован этот метод.

Первым этапом применения МАИ является структурирование проблемы выбора в виде иерархии или сети. В наиболее элементарном виде иерархия строится с вершины (цели), через промежуточные уровни-критерии (технико-экономические параметры) к самому нижнему уровню, который в общем случае является набором альтернатив. [3] На рис. 1.3 представлена схема, структурирующая проблему в виде иерархии.



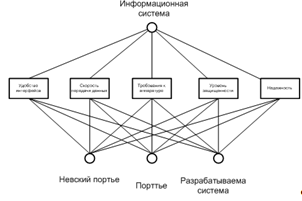
Рис. 1.3. Структурирование проблемы выбора в виде иерархии.

Итак, даны три информационные системы: "Невский портье", "Портье" и "Разрабатываемая система". Определены критерии, по которым должно быть проведено сравнение систем и выбрана наиболее подходящая для описываемой предметной области. Проведем общее сравнение систем по выбранным критериям. Результаты сравнения сведены в табл. 1.4.

Таблица 1.4

Общее сравнение систем-аналогов

Критерии	Невский Портье	Портье	Разрабатываемая система
Удобство интерфейса	Низкое	Среднее	Высокое
Скорость передачи данных	Средняя	Средняя	Высокая
Требования к аппаратуре	Средние	Высокие	Низкие
Уровень защищенности	Низкий	Средний	Высокий
Надежность	Средняя	Средняя	Высокая

---

Начнем с построения матрицы попарных сравнений для критериев, т.е. со второго уровня иерархии (на первом уровне наша цель - выбор информационной системы, на третьем - альтернативы). Заполняя таблицу 1.5, попарно сравниваю критерий из строки с критерием из столбца по отношению к цели - выбору информационной системы. Значения из шкалы относительной важности вписываю в ячейки, образованные пересечением соответствующей строки и столбца. Относительные веса критериев сведены в табл. 1.5. На рис. 1.4 представлена диаграмма, отображающая результаты вычислений.

Таблица 1.5

Сравнение критериев по значимости

Удобство интерфейса	Скорость передачи данных	Требования к аппаратуре	Уровень защищенности	Надежность	Оценка компонентов собственного вектора	Нормализованные оценки вектора приоритета	Max
Удобство интерфейса	1	1/5	1/3	1/9	1/7	0,254	0,032	0,810
Скорость передачи данных	5	1	3	1/5	1/5	0,903	0,115	1,328
Требования к аппаратуре	3	1/3	1	1/7	1/5	0,491	0,063	1,023
Уровень защищенности	9	5	7	1	3	3,936	0,502	0,897
Надежность	7	5	5	1/3	1	2,255	0,288	1,307
Сумма	7,840	5,366

---

 



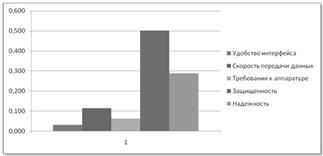
Рис. 1.4. Сравнение критериев оценки ИС

Относительная сила, величина или вероятность каждого отдельного объекта в иерархии определяется оценкой соответствующего ему элемента собственного вектора матрицы приоритетов, нормализованного к единице. Процедура определения собственных векторов матриц поддается приближению с помощью вычисления геометрической средней. Заполнив табл. 1.5, сначала определяются оценки компонент собственного вектора, которые получаются как произведение относительных весов критерия по горизонтали, возведенного в степень 1/5 (где 5 - количество критериев). Например, рассчитаем оценку собственного вектора для критерия "Удобство интерфейса":

(1*1/5*1/3*1/9*1/7*)1/5 = 0,254

Аналогично определяю остальные критерии.

Для того же критерия "Удобство интерфейса" рассчитаем нормализованные оценки вектора приоритета, разделив оценки собственного вектора на их сумму

0,254/7,840=0,032

Так же рассчитываем остальные критерии.

Весьма полезным побочным продуктом теории является так называемый индекс согласованности (ИС), который дает информацию о степени нарушения согласованности. Вместе с матрицей парных сравнений мы имеем меру оценки степени отклонения от согласованности. Если такие отклонения превышают установленные пределы, то тому, кто проводит суждения, следует перепроверить их в матрице.

ИС=(lmax-n)/(n-1)

где lmax - максимальное собственное значение матрицы, n - размерность матрицы.

ИС=(5,366-5)/(5-1)=0,091

Разделив ИС на число, соответствующее случайной согласованности матрицы пятого порядка, равного 1,12, получим отношение согласованности (ОС). Величина ОС должна быть порядка 10% или менее, чтобы быть приемлемой. В некоторых случаях допускается ОС до 20%, но не более, иначе надо проверить свои суждения.

ОС=0,091/1,12=0,082=8,2% < 10%,

т.е пересматривать суждения нет необходимости.

Согласно проведенному анализу и расчетам, сведенным в таблицу, а так же диаграмме, можно сделать вывод, что наибольшее внимание уделяется критерию "Защищенность".

Следующим шагом является выполнение сравнения информационных систем по каждому критерию отдельно. Данные об информационных системах по всем критериям были представлены в табл. 1.

Построим матрицу сравнений, сравнивая попарно альтернативу из строки с альтернативой из столбца по отношению к критерию "Удобство интерфейса". Сравнительные оценки систем по критерию "Удобство интерфейса" сведены в табл. 1.6. Никакие другие критерии при этом не учитываются. Результаты расчётов представлены на рис. 1.5.

---

Таблица 1.6

Сравнение систем по удобству интерфейса

Невский портье	Портье	Разрабатываемая ИС	Оценка компонентов собственного вектора	Нормализованные оценки вектора приоритета	Max
Невский портье	1	1/3	1/3	0,644	0,202	0,336
Портье	3	1	1/3	1,00	0,313	1,356
Разрабатываемая ИС	3	3	1	1,552	0,486	3,399
Итог	3,196	5,090

 

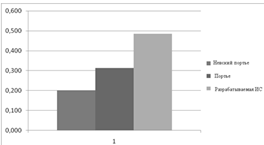
Рис. 1.5. 

---

Смотрите также файлы

• Средняя заработная плата, тыс.docx

• Норматив псп Боевое развертывание на ац с подачей одного гпс 600 на 2 рукава d 77.doc

• Анафилактикалы шок Анафилактикалы шок деп.docx

• Практикум для курсантов обучающихся по специальности.doc

• Итоговая тестовая работа по.docx