Номер периода	Период времени		Число вызовов
времени суток i	суток, ч		за период mi
1	[0;	4)	20
2	[4;	8)	17
3	[8; 12)		20
4	[12;	16)	18
5	[16;	20)	14
6	[20;	24)	25
Всего	[0; 24)		n = 114

4.3. Вычисляется средний уровень ряда динамики, т.е. среднее число вызовов, поступивших в течение четырехчасового периода времени суток:

			I	6
			mi		mi		n
			i1		i1			.	(17)
	m
			I
				6		6

---

Например, по данным табл. 4 среднее число вызовов ПП в городе, поступивших в течение четырехчасового периода времени суток, оказалось равным m = 114 / 6 = 19.
4.4. Динамика числа вызовов ПП по периодам времени суток отображается графически в виде радиальной круговой диаграммы. Для построения диаграммы проводится окружность с радиусом, пропорциональным среднему уровню ряда (m). Окружность делится на равные части по числу членов ряда (т.е. по числу I = 6 выделенных периодов времени в сутках) и из ее центра через конец каждой дуги проводится луч. Лучи последовательно нумеруются в направлении по часовой стрелке. Вдоль каждого луча с порядковым номером i от центра окружности откладывается отрезок, пропорциональный i-му уровню временного ряда m_i (i = 1, 2,..., I). Концы отрезков соединяются замкнутой ломаной линией.
Пример радиальной круговой диаграммы, построенной для города по данным табл. 4, показан на рис. 4.



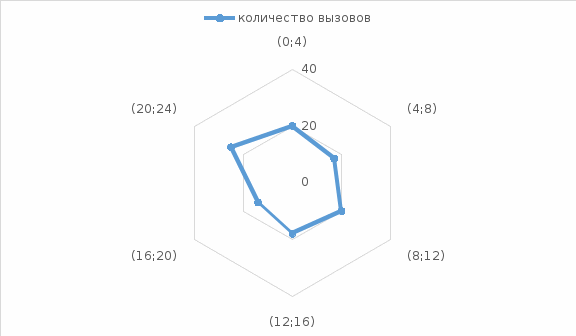
Рис.4. Радиальная круговая диаграмма динамики числа вызовов пожарных подразделений в городе по четырехчасовым периодам времени суток

Таблица 5

---

Распределение числа вызовов пожарных подразделений в городе

по месяцам 2020 года

Номер месяца j	Месяц года	Число mi вызовов
1	Январь	27
2	Февраль	31
3	Март	33
4	Апрель	23
Всего	2020 год	n = 114

Изобразим динамику числа вызовов ПП в городе по месяцам года графически в виде столбиковой диаграммы. Столбики на диаграмме, имеющие одинаковую ширину, соответствуют различным месяцам, а высота каждого столбика пропорциональна соответствующей частоте (числу вызовов ПП). Диаграмма может изображаться с сомкнутыми или с разомкнутыми столбиками.
На рис. 5 представлена построенная по данным табл. 5 столбиковая диаграмма, отображающая динамику числа вызовов ПП в городе по месяцам года.



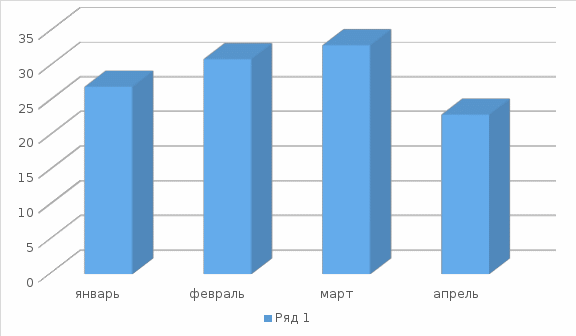
Рис. 5. Динамика числа вызовов пожарных подразделений в городе по месяцам года

5. 
   Проведем анализ изменчивости в уровнях временного ряда числа вызовов пожарных подразделений (ПП) в городе по месяцам года.
   

5.1. Исходными данными для анализа служат значения m_j числа вы-зовов ПП за разные месяцы года (j =1, 2, 3,..., J), подсчитанные по диспетчерскому журналу в процессе выполнения задания 4 и представленные в табл. 7 (по учебному диспетчерскому журналу статистическое исследование проводится лишь за четыре месяца года, то есть

---

J = 4).
Месяцы года содержат разное количество суток T_j, поэтому корректно сравнивать между собой не число m_j вызовов ПП в разные месяцы, а среднесуточное число Y_j вызовов ПП за разные месяцы, расчет которого производится по формуле

Yj m j Tj,

Исходные данные и результаты расчета среднесуточного число Y_j вызовов ПП для города Бор за разные месяцы года представлен в табл.6.
5.2. Производится расчет значений комплекса специальных показателей, характеризующих изменчивость в уровнях временного ряда (также называемого рядом динамики) и используемых для анализа временных рядов. В основе расчета показателей изменчивости лежит сопоставление того или иного уровня Y_j временного ряда с некоторым уровнем Y_баз, принятым за базу для сравнения. В качестве базового уровня Y_баз можно принять предшествующий уровень Y_j-1, начальный уровень Y₁ или средний уровень временного ряда Y.


Таблица 6
Показатели изменчивости уровней временного ряда среднесуточного числа вызовов пожарных подразделений в городе за четыре месяца 2020 года

Показатели изменчивости	Значения показателей за j-й месяц
уровней ряда динамики (цепные)	Январь	Февраль	Март	Апрель
	(j = 1)	(j= 2)	(j = 3)	(j = 4)
Число mj вызовов за j-й месяц	27	31	33	23
Число суток в j-м месяце	31	29	31	30
Среднесуточное число Yj вызовов за j-й месяц	0,871	1,068	1,064	0,766
Абсолютный прирост Aj = Yj - Yj -1	-	+0,197	+0,193	-0,105
Коэффициент роста Hj = Yj /Yj -1	-	1,226	1,221	0,879
Темп роста (%)	-	122,6	122,1	87,9
Коэффициент прироста Bj = Aj /Yj-1	-	0,226	0,221	-0,121
Темп прироста (%)	-	+22,6	+22,1	-12,1

---

• 
  показателям изменчивости относятся: абсолютный прирост, коэффициент (или темп) роста, коэффициент (или темп) прироста. Расчет этих показателей производится для каждого j-го месяца (j = 1, 2, ..., J), которому соответствует значение j-го уровня ряда Y_j.
  

Абсолютный прирост (A_j)определяется как разность между рассматриваемым уровнем ряда (Y_j) и уровнем, принятым за базу для сравнения
(Y_баз):

Aj Yj Yбаз = 1,068-0,871 = +0,197.

Значения абсолютного прироста A_i могут быть положительными (при Y_j> Y_баз),отрицательными(при Y_j< Y_баз),либо равными нулю(при Y_j=

Y_баз).
Коэффициент роста (H_j)определяется как отношение рассматриваемого уровня ряда (Y_j) к уровню, принятому за базу для сравнения (Y_баз):

• 
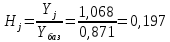
  зависимости от соотношений значений рассматриваемого и базового уровней значение коэффициента роста H_j может оказаться меньше еди-
  

ницы (при Y_j < Y_баз), равным единице (при Y_j = Y_баз) или больше единицы (при Y_j > Y_баз).
Коэффициент роста, выраженный в процентах, называется темпом роста.

Коэффициент прироста (B_j)определяется как отношение абсолютно-

го прироста (Aj) к уровню, принятому за базу для сравнения (Yбаз):

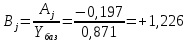
Произведем расчет следующих обобщенных показателей, которые используются при анализе временных рядов:
– средний уровень ряда (Y ), вычисляется по формуле:



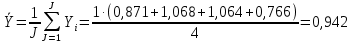
– стандарт ряда (S_Y), вычисляется по формуле:



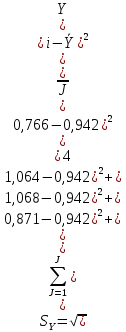
– коэффициент вариации ряда (ν), вычисляется по формуле:

---

Смотрите также файлы

• Инструкция Один человек выполняет подтягивания, другие участники ведут счет и время. Далее используя необходимые расчеты, определяют мощность.docx

• Фотосинтез и хемосинтез.doc

• Анамнез 1) Были ли вирусные инфекции (эпид паротит, вирусный гепатит, энтеровирус Коксаки В, инф мононуклеоз, краснуха, ветряная оспа, герпес, цмв, корь, грипп).docx

• Политологи я.ppt

• Педагогика оулы ббк 74. 00 П24.doc