Файл: Расчет химического равновесия по табличным термодинамическим данным Формулировка задачи.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 44
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Для анализа полученной зависимости нужно воспользоваться следующим дифференциальным уравнением:
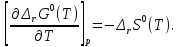(7)В нашем расчете изменение энтропии реакции (I) во всем расчетном интервале температур больше нуля. Следовательно, производная уравнения (7) отрицательна, что делает
убывающей функцией при росте температуры. Рисунок 4 это иллюстрирует.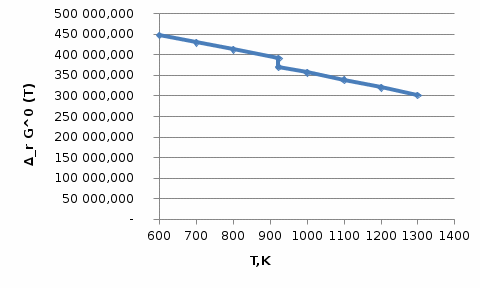
Рисунок 4 – Зависимость изменения энергии Гиббса реакции (I) от температуры
7. Расчет константы равновесия
Константа равновесия реакции (I) определяется из уравнения
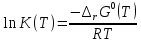. Расчет представим таблицей 6 и графиком (рисунок 5).Таблица 6 – Расчетные значения
реакции (I)| T, K | | 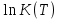| K(T) |
| 600 | 447 139,197 | -89,68 |  |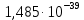
| 700 | 429 534,850 | -73,84 |  |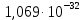
| 800 | 411 956,028 | -61,97 |  |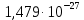
| 923 | 390 338,875 | -50,89 |  |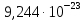
| 923 | 370 381,350 | -48,29 |  |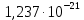
| 1000 | 356 336,551 | -42,88 |  |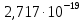
| 1100 | 338 085,480 | -36,99 |  |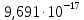
| 1200 | 319 817,340 | -32,07 |  |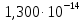
| 1300 | 301 527,006 | -27,91 |  |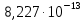
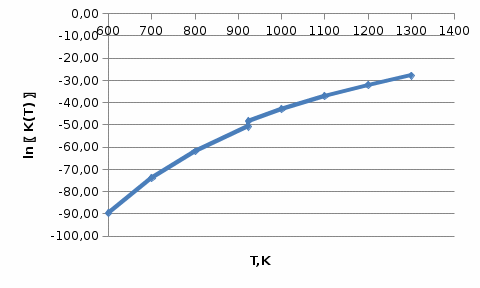
Рисунок 5 – Зависимость
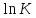реакции (I) от температурыНа рисунке 5 изображена логарифмическая зависимость константы равновесия реакции (I) по двум причинам: во-первых, этот график более нагляден; во-вторых, температурная зависимость константы равновесия реакции (I) – логарифмическая и описывается уравнением Вант-Гоффа:
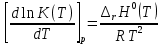. (8)Анализируя уравнение (8) приминительно к реакции (I), подтверждаем результаты нашего расчета: константа равновесия должна быть возрастающей функцией при увеличении температуры, так как
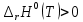.8. Расчет равновесного состава газовой фазы
В реакции присутствует одно газообразное вещество. При условии, что обш=щее давление системы постоянно (1 атм), необходимость расчета газовой фазы отпадает. Давление газообразного участника реакции при любой температуре равно 1 атм.
Расчет завершен. Поставленная задача выполнена. Для реакции
имеется весь набор термодинамических характеристик в интервале 600-1300 К и можно судить о ее направлении. Самопроизвольность процесса при условии
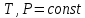определяется по второму закону термодинамики для необратимых процессов:
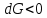(9)Неравенство (9) говорит о том, что если изменение энергии Гиббса положительно, то процесс в системе протекает обратимо. Обратимые процессы не могут протекать самопроизвольно в прямом направлении, однако обратная реакция идет самопроизвольно. Для системы с химической реакцией это означает, что исходные вещества не взаимодействуют друг с другом, и реакция протекает в обратном направлении.
.
9. Вывод
В интервале температур 600-1300 К изменение энергии Гиббса реакции M
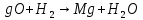положительно. Реакция протекает в обратном направлении.С практической точки зрения, на основании расчета, делаем следующее заключение: получить магний по реакции (I) можно, если систему нагреть до температуры не менее 600 К, а при 923 К магнийй изменит свое агрегатное состояние с твердого на жидкое.