Файл: Практикум (оудістемелік нсаулы) Шымкент 2018.docx

7. Штангенциркульдің (немесе микрометрдің) көмегімен серіппенің d диаметрін 5 рет өлшеңіз (серіппенің әртүрлі жерлерінде), бұл ретте серіппені оның бойлық осінің бойымен қолмен қысу керек. Жүргізілген өлшеулердің орташа мәні 1 кесте.

8. Микрометрдің көмегімен серіппенің әр түрлі жерлерінде 5 рет жасалған d сым диаметрін өлшеңіз. Жүргізілген өлшеулердің орташа мәнін 1-кестеге енгізіңіз.

9. Серіппе орамдарының N санын санаңыз.

10. Тербеліс кезеңін мына формула бойынша есептеңіз

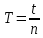
11. G жылжыту модулін келесі формуламен есептеңіз:

12. Формуланы пайдалана отырып жылжу модулін анықтаудың салыстырмалы қателігін бағалаңыз есептеу кезінде осы теңдікті пайдалануға болады
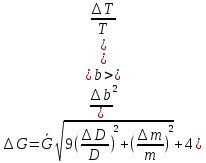
2 жаттығу . Серіппені созу әдісімен жылжу модулін анықтау.

1. 9 кронштейнін фотодатчикпен алып тастаңыз.

2. Серіппеге жинақ жүктің негізін 8 іліп, 6 сызғыштың көмегімен жүктің төменгі жазықтығының орналасуын Xo байқаңыз .

3. Оқытушының нұсқауы бойынша жиынтық жүктің негізіне салмағы m1 жүкті ілу. 6 сызғыштың көмегімен жүктің төменгі жазықтығының орналасуын өлшеу X1 . Алынған мәндерді 2-кестеге енгізіңіз.

4. m2= 2 m1 массасы жүкті серіппеге іліп қою . Сызғыштың көмегімен жүктің төменгі жазықтығының орналасуы X2 . Алынған мәндерді 2-кестеге енгізу.

5. m3= 3m1 салмағы бар жүкті серіппеге іліп қойыңыз . Сызғыштың көмегімен жүктің төменгі жазықтығының орналасуын X3 байқаңыз . Алынған мәндерді 2-кестеге енгізіңіз..

2-кесте.

№	m,кг		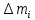х, мм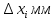
Серіппе 1,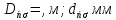
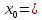1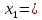
2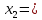
3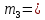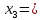
Серіппе 2,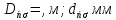
1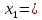
2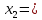
3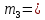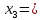

---

6. Серіппенің ұзаруын мына формула бойынша анықтау:

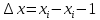
7. Формуланы пайдаланып 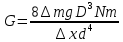серіппені созған кезде жылжу модулін есептеу, мұнда 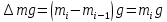серіппені созатын күш; N –серіппенің орамдарының саны; D серіппенің орташа диаметрі; d – сымның орташа диаметрі. Алынған мәліметтерді 2-кестеге енгізіңіз.

8. G-ның орташа мәнін және салыстырмалы қателігін есептеңіз мына формула арқылы есептеңіз.



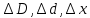тікелей өлшеулердің қателігі ретінде табылады. 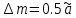(Стьюдент әдісі бойынша)

9. Басқа серіппе үшін 1-8 тармақтарын қайталаңыз.
Бақылау сұрақтары

1. Деформация түрлерін атаңыз.

2. Дене ішінде, серпімді және пластикалық деформацияларда пайда болатын күштер қандай болады?

3. Бұл деп аталады жылжуымен?

4. Бұл кернеуі деп аталады? Қалыпты кернеу модуліне формуланы жазыңыз. Жанама кернеу модулі үшін формуланы жазыңыз.

5. Серпімділік модульдерін атаңыз.

6. Материалды жылжыту модулі нені сипаттайды?

7. Созылу (сығылу) деформациясы үшін Гук заңын жазыңыз.

8. Жылжу деформациясы үшін Гук заңын жазыңыз.

9. Созылу деформациясы (сығылу) кезінде абсолюттік ұзаруы үшін Гук заңын жазыңыз.

10. Неге серіппенің ұзаруы бойынша жылжыту модулін табуға болады?

11. Серіппелі маятник дегеніміз не?

12. Циклдік жиілікке және серіппелі маятниктің тербеліс кезеңіне арналған формулаларды жазыңыз.

13. Материалдың Юнг модулі нені сипаттайды?

Әдебиет

1. Савельев И. В. 4 томдық жалпы физика курсы. Механика. Молекулалық физика және термодинамика: оқу құралы / И. В. Савельев; жалпы ред.В. И. Савельева. – М.: КНОРУС, 2009. 2.9, с.73-77.

2. Т. И. Трофимова. Физика курсы. Мәскеу. "Қазақстан жоғары мектебі". 2007, § 21, с. 42-45.

3. Қойшыбаев а. А., Яворский Б. М. физика Курсы. М.: Жоғары. мектеп, 2000, § 1.1, 1-т., 8-Б.; § 29.3, 2-т., 391-Б.; § 29.1, 3-т., 386-Б.
№9 зертханалық жұмыс

---

Сұйықтың тұтқырлық коэффициентін Стокс тәсілімен анықтау
Жұмыстың мақсаты: қарастырылып отырға нтәсілдің теориясымен танысу, өлшеу әдістерін меңгеру және кейбір себептердің эксперимент нәтижесіне тигізетін ықпалына талдау жасау.

Қажеттіқұрал-жабдықтар: таянышқа орнатылып, ішіне зерттелетін сұйыққұйылған цилиндр пішінді шыныыдыс, масштабты сызғыш, кішкене металл шарлар, секундөлшегіш.
Теориядан қысқаша түсінік

Тұтқырлық (ішкі үйкеліс) деп, аққыш денелердің (сұйық пен газдың) бір қабатынан екінші қабатына дененің орынауыстыруына кедергі жасайтын қасиетін айтамыз.
Сұйықтың жоғарғы және төменгі қабаттарын өзара параллель жазық екі пластина ж 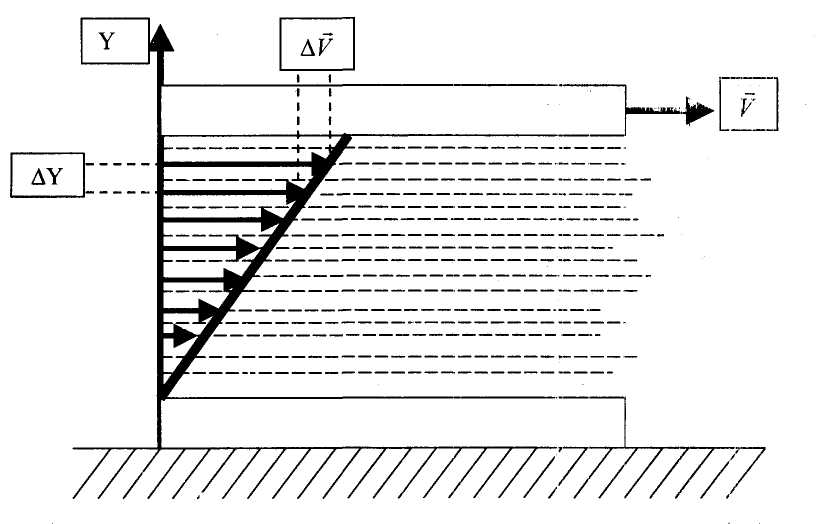әне олсол сияқты жұқа қабаттардан тұрады деп қарастырайық. (1- сурет). Егер жоғары пластинаны, төменгі пластинаға қатысты солдан оңға қарай жылжытсақ, онда оған жабысқан сұйық молекулалары пластинамен бірге дәл сондай жылдамдықпен қозғалады. Бұл молекулалар келесі қабаттың молекулаларын

1-сурет

ілестіреді де, процесс осылайша одан әрі жалғаса береді. Төменгі пластинаға жанасып жатқан молекулалар қабаты тыныштықта болады да, басқа қабаттар бірінің бетімен бірі сырғи отырып, орын ауыстырады. Төменгі қабаттан алыстаған сайын молекулалар қабатының жылдамдығы арта түседі. Сұйықтың тұтқырлығы жанасқан қабаттардың бір-біріне қарағанда ығысуына кедергі жасайтын күштің пайда болуы нәтижесінде байқалады. Бұл күштің табиғатын былай түсіндіруге болады: әртүрлі жылдамдықпен қозғалған сұйық қабаттары бір-бірімен молекулалар ауысады. Сонда жылдам қозғалатын қабаттағы молекулалар біраз қозғалыс мөлшерін баяу қозғалатын қабатқа береді. Ал баяу қозғалатын қабаттан шапшаң қозғалатын қабатқа өткен молекулалардың қозғалыс мөлшері артады. Соның нәтижесінде шапшаң қозғалатын молекулалар жылдамдығы баяулайды. Ал, ішкі үйкеліс күші сұйыққа баттарының қозғалу жылдамдықтарын теңестіруге тырысады. Сұйықтың тұтқырлығынан пайда болған кедергінің шамасы сұйық қабаттары жылдамдықтарының айырымына және олардың ара кашықтығына байланысты болады. Бір қабаттан екінші қабатқа өткен сұйық жылдамдығының өзгерісі артқан сайын, ішкі үйкелістің шамасы да артады. Сұйықтың көршілес екі қабатының жылдамдықтар айырымы сол қабаттардың жылдамдық бағытына түсірілген нормаль бойымен есептелінген ара қашықтығына ∆Ү қатынасының шегі:

---

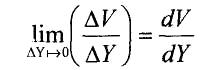
Жылдамдықградиентідепаталады.

Ламинарлық (құйынсыз) ағыста сұйықтың екі қабатының арасына әсер ететін ішкі үйкеліс күші олдардың жанасу бетінің ауданы мен жылдамдық градиентіне тура пропорционал болады:

- Ньютон формуласы (1)
Мұндағы сұйықтың табиғатына және оның күйіне (мысалы температурасына) байланысты болатын шама η – ішкі үйкеліс коэффициенті немесе динамикалық тұтқырлық коэффициентідепаталады.

Сұйықтың динамикалық тұтқырлығының, тығыздығына қатынасын кинематикалық тұтқырлық деп атаймыз: υ = η/ρ

Егер (1) формуладан dV/dY=1 жәнеS= 1 деп алсақ, онда η= F. Яғни тұтқырлық, сан жағынан, бір-бірімен салыстырғанда жылдамдық градиенті бірге тең қозғалыстағы екі қабаттың жанасу бетінің әрбір бірлік ауданында пайда болатын ішкі кедергі күшіне тең. СИ жүйесінде тұтқырлық бірлігі үшін модулі 1 м/с жылдамдық градиенті 1м жана су бетінде 1Н ішкі үйкеліс күшін туғызатын тұтқырлық алынады. Бұл бірлік Паскаль-секунд (Па·с) деп аталады. Тұтқырлық коэффициенті температураға тәуелді. Сұйық пен газ үшін бұл тәуелділіктің елеулі айырмашылығы баp. Сұйық температурасы жоғарылаған сайын оның тұтқырлығы күрт азаяды. Газда керісінше, температура жоғарылаған сайын тұтқырлық коэффициенті артады. Η коэффициентінің температураға байланысты бұлай өзгеруін сұйық пен газдың ішкі үйкеліс механизмінің әртүрлі болуынан деп түсіну қажет.

Кішкене шардың сұйық ішіндегі қозғалысы.

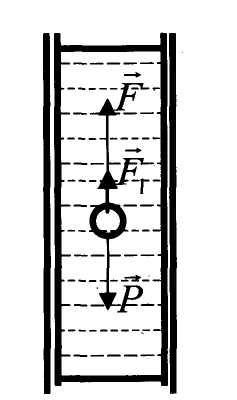
Сұйықтыңтұтқырлықкоэффициентінкішкенешардыңтұтқырортадағықозғалысы (Стокс тәсілі) бойынша анықтауға болады. Енді кішкене шардың тыныштықта тұрған тұтқыр сұйықтағы еркін түсуін қарастырайық (2-cypeт). Бұл жағдайда оған үш күш әсер етеді:

(2)
А уырлық күші: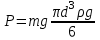

2-сурет
мұндағы d – кішкене шардың диаметрі, 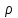- кішкене шардың

тығыздығы, g-еркін түсу үдеуі.
Кері итеруші күш (Архимед заңыбойынша):

---

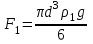
(3)

мұндағы ₁ - сұйық тығыздығы.

Сұйық қабаттардың арасындағы ішкі үйкеліс күшінің әсерінен пайда болатын, қозғалысқа қарсы бағытталған күш кедергі күші. Кішкене шардың бетіне жанасып тұрған сұйық қабат оған жабысады да, шармен бірге сондай жылдамдықпен қозғалады. Шарға жақын, іргелес жатқан сұйық қабаттары да қозғалысқа келеді. Бірақ кішкене шардан алыстаған сайын, сұйық қабаттарының жылдамдығы азая береді. Сондықтан ортаның кедергі күшін есептегенде, сұйық пен кішкене шар арасындағы үйкелісті ескермей-ақ, сұйық қабаттарының арасындағы үйкелісті есепке алу керек. Тәжірибе ортаның кедергі күші дененің қозғалыс жылдамдығына, оның геометриялық пішініне, сызықтық өлшемдеріне, бетінің күйіне және ортаның тұтқырлығына байланысты болатынын көрсетеді. Егер кішкене шар жан-жаққа шексіз жайылып жатқан сұйық ішінде, ешқандай құйын тудырмай (түсу жылдамдығы аз кішкене шар) түсетін болса онда Стокстың есептеуі бойынша кедергі күші мынаған тең:

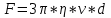(4)

мұндағы η-сұйықтық тұтқырлық коэффициенті, υ –кішкене шардың жылдамдығы, d - оның диаметрі.

Үш күш те вертикаль бойымен: ауырлық күші төмен, ал кері итеруші күш пен кедергі күші жоғары қарай бағытталған.(2 - сурет)

Бастапқы кезде кішкене шардың жылдамдығы арта түседі оның жылдамдығы артқан сайын кедергі күші де артады. Сәлден соң, ауырлық күшін (Р), Ғ және Ғ₁ күштердің қосындысы теңгереді. Сол мезеттен бастап, барлық күштердің қорытқы күші нөлге теңеледі, яғни:

Р-(Ғ₁ +Ғ) = 0 (5)

Әрі қарай кішкене шар υ=υ₀ жылдамдықпен бір қалыпты қозғалады. Мұндағы, тұтқырлық коэфицентін (5) формуладағы P,F₁және Ғ шамаларының мәңдерін қойып төмендегіше табуымызға болады:



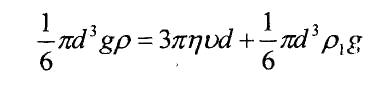
немесе:


б ұдан: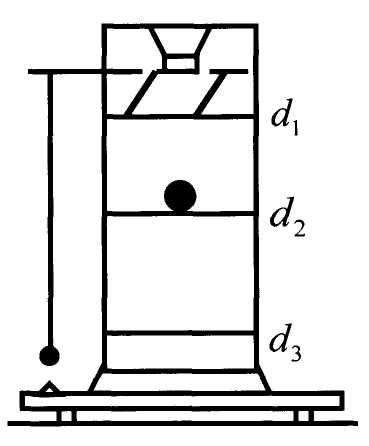




Кішкене шардың жылдамдығын l /τқатынасымен ауыстырсақ (мұндағы l -жол, τ-шардың бір қалыпты түсу уақыты), тұтқырлық коэффициентін есептеуге мүмкіндік беретін төмендегі өрнекті табамыз:

---