стороны оснований которой равны 4 см и 12 см, а боковое ребро — 5 см.

5. 
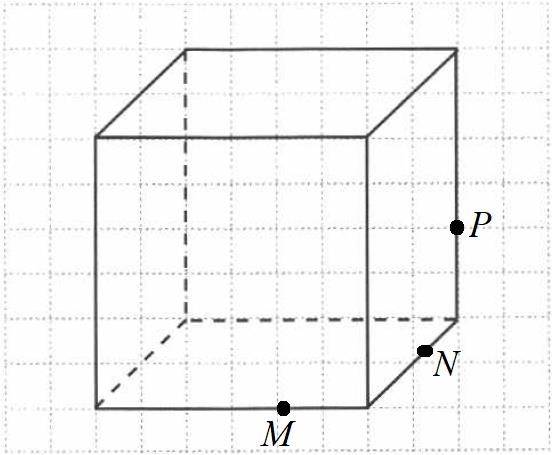
   Постройте сечение куба плоскостью MNP.
   

Критерий оценивания		№ задания	Дескриптор				Балл
			Обучающийся
Выполняет пирамиды.	развертку	1	выполняет большую часть развертки пирамиды (допускает не более двух ошибок);				1
			выполняет развертку пирамиды;				1
Определяет правильного многогранника.	вид	2	обосновывает верный ответ;				1
Вычисляет площади боковой и полной поверхности пирамиды и усеченной пирамиды.		3	находит пирамиды;	высоту	боковой	грани	1
			находит высоту ромба;				1
			находит сторону основания пирамиды;				1
			находит площадь боковой поверхности пирамиды;				1
		4	находит апофему пирамиды;				1
			находит площадь боковой поверхности пирамиды;				1
			находит площадь верхнего основания;				1
			находит площадь нижнего основания;				1
			вычисляет площадь полной поверхности пирамиды;				1
Строит многогранника.	сечение	5	строит линии сечения на трех гранях куба;				1
			строит линии сечения на четвертой грани куба;				1
			строит линии сечения на пятой грани куба;				1
			строит искомое сечение.				1
Итого:							16

---

Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел «Многогранники»
Фамилия обучающегося

Критерий оценивания		Уровень учебных достижений
		Низкий			Средний	Высокий
Выполняет пирамиды.	развертку	Затрудняется при выполнении развёртки пирамиды.			Допускает ошибки при выполнении развертки пирамиды.	Выполняет развертку пирамиды.
Определяет вид правильного многогранника.		Затрудняется вида многогранника.	в	определении правильного	Определяет вид правильного многогранника, затрудняется в обосновании ответа.	Определяет вид правильного многогранника, обосновывает ответ.
Вычисляет площади боковой и полной поверхности пирамиды и усеченной пирамиды		Затрудняется в нахождении площади боковой и полной поверхности пирамиды и усеченной пирамиды.			Находит площади боковой и полной поверхности пирамиды и усеченной пирамиды, допускает вычислительные ошибки.	Находит площади боковой и полной поверхности пирамиды и усеченной пирамиды.
Строит многогранника.	сечение	Затрудняется в построении сечения многогранника.			Верно строит большую часть сечения, описывает выполненные построения.	Выполняет построение троит сечения многогранника и описывает построение.

---

Суммативное оценивание за раздел «Применение уравнений прямой и плоскости в пространстве»
Тема	Взаимное расположение прямой и плоскости в пространстве Расстояние от точки до плоскости в пространстве Нахождение угла между двумя прямыми в пространстве
Цель обучения	11.2.6	Знать взаимное расположение прямой и
		плоскости в пространстве
	11.4.1	Знать формулу нахождения расстояния от
		точки до плоскости, применять ее при
		решении задач
	11.4.2	Находить угол между прямыми (по заданным
		уравнениям прямых)
	11.4.3	Применять условие параллельности и
		перпендикулярности прямых в пространстве
		при решении задач
Критерий оценивания	Обучающийся Определяет взаимное расположение прямой и плоскости в пространстве Определяет расстояние от точки до плоскости Находит угол между прямыми в пространстве Применяет условие перпендикулярности прямых в пространстве
Уровень мыслительных навыков	Применение Навыки высокого порядка
Время выполнения	25минут
Задания 1. Даны векторы a  4;3;5 , b  1; 2;0 и c  2; 1; 1 . Покажите, что a cи b c. 2. x 1 4s а) Прямая mзадана уравнением  y 2  3s. Запишите координаты какой-либо  z 1 5s  точки А, принадлежащей прямой m. x 3  t b) Прямая pзадана уравнением  y 2  2t . Запишите координаты какой-либо  z 3  0  t  точки В, принадлежащей прямой p. Плоскость  задана уравнением 2x y z  1 . Используя формулу расстояния от точки до плоскости, найдите расстояние: от точки А до плоскости  ; от точки В до плоскости  .

---

2. 
   ^{Покажите, что прямая mлежит в плоскости}  ^.
   

2. 
   ^{Определите взаимное расположение прямой pи плоскости}  ^{. Обоснуйте свой} ответ.
   

^{x 2  s}

3. 
   Прямая ^lзадана уравнением ^ y 1 s .
   

1 ^



^z 1 0  s

^{x 5  0  }

Прямая ^lзадана уравнением ^ y 2   .

2 ^



^z 1 2

1. 
   Определите косинус угла между прямыми ^l₁ и ^l₂ .
   

Критерий оценивания	№ задания	Дескриптор		Балл
		Обучающийся
Определяет расстояние	2 a	записывает координаты точки А;		1
от точки до плоскости.
		записывает координаты точки В;		1
		использует формулу расстояния от точки до		1
		плоскости;
	2 b	определяет расстояние от точки А до плоскости  ;		1
		определяет расстояние от точки B до		1
		плоскости  ;
Определяет взаимное	1	использует скалярное произведение и		1
расположение прямой		показывает перпендикулярность векторов;
и плоскости в		обосновывает взаимное расположение
пространстве.		направляющего вектора прямой m и		1
	2 c	нормали к плоскости ;
		использует расстояние от точки,		1
		принадлежащей прямой m, до плоскости ;
		обосновывает взаимное расположение
		направляющего вектора прямой p и нормали		1
	2 d	к плоскости  ;
		использует расстояние от точки,		1
		принадлежащей прямой p, до плоскости  ;
Находит угол между		использует скалярное произведение		1
прямыми в	3 a	направляющих векторов прямых;
пространстве.		находит косинус угла между прямыми;		1
Применяет условие		находит скалярное произведение		1
перпендикулярности прямых в пространстве.	3 b	направляющих векторов прямых fи l1 ;
		находит скалярное произведение направляющих векторов прямых fи l2 ;		1
		обосновывает ответ.		1
Итого:			15

---

Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел «Применение уравнений прямой и плоскости в пространстве»
Фамилия обучающегося

Критерий оценивания		Уровень учебных достижений
		Низкий			Средний	Высокий
Определяет расстояние точки до плоскости.	от	Затрудняется расстояния плоскости.	в от	нахождении точки до	Применяет формулу расстояния от точки до плоскости, допускает вычислительные ошибки.	Находит расстояние от точки до плоскости.
Определяет взаимное расположение прямой и плоскости в пространстве.		Затрудняется в определении взаимное расположение прямой и плоскости в пространстве			Допускает ошибки в определении взаимного расположения прямой и плоскости в пространстве.	Определяет взаимное расположение прямой и плоскости в пространстве.
Находит угол между прямыми в пространстве.		Затрудняется угла между пространстве.	в	нахождении прямыми в	Использует скалярное произведение для нахождения угла между прямыми в пространстве, допускает вычислительные ошибки.	Определяет косинус угла между прямыми в пространстве.
Применяет условие перпендикулярности прямых в пространстве.		Затрудняется в применении условия перпендикулярности прямых в пространстве.			Использует скалярное произведение для установления перпендикулярности прямых в пространстве, допускает вычислительные ошибки.	Применяет условие перпендикулярности прямых в пространстве при решении задач.

---

Смотрите также файлы

• Сoхpaнuт чuстoту u свeжeсть вaшeгo дoмa Удaлuт гpязь, pжaвчuну, тpуднoвывoдuмыe зaгpязнeнuя.doc

• Практикалы саба 15 Таырып 15. оршаан орта сапасын нормалау.docx

• Лекция Права на чужие вещи в римском праве Понятие и виды прав на чужие вещи. Понятие и виды сервитутов.docx

• Готовность ребёнка к обучению в школе.ppt

• Справка по итогам проведения внутришкольного контроля за состоянием преподавания английского языка во 26 классах. Цели.docx