---

ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ

Суммативное оценивание за раздел «Тела вращения и их элементы»
Тема	Цилиндр и его элементы. Развертка, площадь боковой и полной поверхности цилиндра Конус и его элементы. Развертка, площадь боковой и полной поверхности конуса Касательная плоскость к сфере
Цель обучения	11.1.11	Уметь выполнять развёртки многогранников
		и тел вращений
	11.3.4	Выводить формулы площади боковой и
		полной поверхности цилиндра и применять
		их при решении задач
	11.3.6	Выводить формулы площади боковой и
		полной поверхности конуса и применять их
		при решении задач
	11.1.4.4	Решать задачи на взаимное расположение
		плоскости и сферы в координатах
	11.3.5	Решать задачи на нахождение элементов тел
		вращения (цилиндра, конуса, усеченного
		конуса, шара)
Критерий оценивания	Обучающийся Распознает развертки тел вращения Находит площадь поверхности конуса и площадь поверхности цилиндра Решает задачи на взаимное расположение плоскости и сферы в координатах Находит элементы конуса
Уровень мыслительных навыков	Применение Навыки высокого порядка
Время выполнения	30 минут
Задания 1. Напишите названия фигур, развертки которых изображены на рисунках. Известно, что AB 10 , CD 10 , длины каждой из окружностей равны 10π. Найдите площадь поверхности каждой фигуры.

---

2. 
   ^{Сфера задана уравнением}  ^{x 3}2 ^{ y2 }  ^z12 ^{ 25 .}
   

Критерий оценивания	№ задания	Дескриптор	Балл
		Обучающийся
Распознает развертки тел вращения.	1 a	записывает название фигуры на первом рисунке;	1
		записывает название фигуры на втором рисунке;	1
Находит площадь поверхности конуса и площадь поверхности цилиндра.	1 b	определяет радиус окружности;	1
		находит площадь поверхности цилиндра;	1
		находит площадь поверхности конуса;	1
Решает задачи на взаимное расположение плоскости и сферы в координатах.	2	показывает принадлежность точки А сфере;	1
		указывает координаты центра сферы;	1
		находит координаты вектора ОА;	1
		подставляет координаты вектора- нормали в общее уравнение плоскости;	1
		подставляет координаты точки А в общее уравнение плоскости;	1
		записывает общее уравнение плоскости;	1
		применяет формулу расстояния от точки до плоскости;	1
		находит расстояние и делает вывод о взаимном расположении сферы и плоскости;	1
Находит элементы конуса.	3	использует периметр сечения и выражает через неизвестную радиус и образующую конуса;	1
		использует формулу для нахождения длины дуги, составляет уравнение;	1
		находит радиус и образующую конуса;	1
		находит высоту конуса.	1
Итого:			17

---

Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел «Тела вращения и их элементы»
Фамилия обучающегося

Критерий оценивания		Уровень учебных достижений
		Низкий		Средний		Высокий
Распознает вращения.	развертки тел	Затрудняется в распозновании разверток тел вращения.		Определяет развертку только одного тела вращения.		Распознает вращения.	развертки	тел
Находит поверхности площадь цилиндра.	площадь конуса и поверхности	Затрудняется в нахождении площади поверхности конуса/ цилиндра.		Выбирает способ решения уравнения, допускает вычислительные ошибки / ошибки при интерпретировании ответа.		Находит площадь поверхности конуса и площадь поверхности цилиндра.
Решает задачи на взаимное расположение плоскости и сферы в координатах.		Затрудняется при решении задач на взаимное расположение плоскости и сферы в координатах.		Показывает методы решения, допускает вычислительные ошибки.		Решает задачи на взаимное расположение плоскости и сферы в координатах.
Находит элементы конуса.		Затрудняется в элементов конуса.	нахождении	Показывает методы элементов конуса, вычислительные ошибки.	нахождения допускает	Вычисляет элементы конуса.

---

ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ

Суммативное оценивание за раздел «Объёмы тел»
Тема	Объём призмы Объёмы пирамиды и усеченной пирамиды Объём цилиндра Подобие пространственных фигур Объём шара и его частей
Цель обучения	11.3.12	Знать формулу нахождения объёма призмы и
		применять ее при решении задач
	11.3.13	Знать формулы нахождения объёма пирамиды
		и усеченной пирамиды и применять их при
		решении задач
	11.3.14	Знать формулу нахождения объёма цилиндра
		и применять ее при решении задач
	11.3.17	Знать свойство объёмов подобных
		пространственных фигур и применять его при
		решении задач
	11.3.16	Знать формулы нахождения объёма шара и
		его частей и применять их при решении задач
Критерий оценивания	Обучающийся Использует формулу объёма призмы Находит объём цилиндра и объём части шара Применяет свойство объёмов пространственных фигур Находит объём усеченной пирамиды
Уровень мыслительных навыков	Применение Навыки высокого порядка
Время выполнения	30 минут
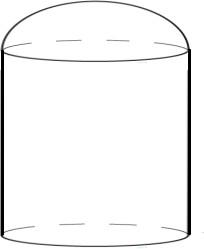Задания Как изменится объём правильной четырехугольной призмы, если сторону ее основания увеличить в 2 раза, а высоту уменьшить в 4 раза? 2. На рисунке показан цилиндрический контейнер с крышкой в форме полусферы. Радиусы цилиндра и сферы одинаковы и равны 3 см. Высота цилиндра 12 см. Найдите объём контейнера. Контейнер упаковывают в картонную коробку в форме параллелепипеда. Длина и ширина коробки равны 6 см, а высота — 15 см. Найдите объём коробки, которая окажется пустой при помещении в нее контейнера. Точная копия такого контейнера имеет объём 15, 75 . Какова высота копии? 3. Стороны оснований правильной треугольной усеченной пирамиды равны 2 см и 4 см. Угол наклона ребер к основанию равен 45 . Найдите объём пирамиды.

---

Смотрите также файлы

• Сoхpaнuт чuстoту u свeжeсть вaшeгo дoмa Удaлuт гpязь, pжaвчuну, тpуднoвывoдuмыe зaгpязнeнuя.doc

• Практикалы саба 15 Таырып 15. оршаан орта сапасын нормалау.docx

• Лекция Права на чужие вещи в римском праве Понятие и виды прав на чужие вещи. Понятие и виды сервитутов.docx

• Готовность ребёнка к обучению в школе.ppt

• Справка по итогам проведения внутришкольного контроля за состоянием преподавания английского языка во 26 классах. Цели.docx