Файл: Конспект лекций Дисциплина Статистика.doc

3. Балансовый метод изучения взаимосвязи.
Статистический баланс представляет собой систему показателей, которая состоит их 2-х сумм абсолютных величин, связанных между собой законом равенства:

Эту сумму можно представить следующим равенством: остаток на начало + приход = расход + остаток на конец.

Товары	Остаток на 1.01	Приход за квартал	Итого (баланс)	Продано в розницу	Продано оптом	Итого в расход	Остаток на 1.04	Баланс
А	1	2	3	4	5	6	7	8
1	5	12	17	8	3	11	6	17
2	8	15	23	18	-	18	5	23
3	2	8	10	5	2	7	3	10
Итого			50					50

Балансовый метод дает возможность не только анализировать показатели во взаимосвязи, но и осуществлять взаимный контроль данных и рассчитывать недостающие показатели.

Пример, продано в розницу = остаток на начало + приход – продано оптом – остаток на конец.
4. Измерение тесноты связи между атрибутивными признаками.
Коэффициент взаимной сопряженности Чупрова.
Для измерения тесноты связи согласованного варьирования атрибутивных варьирующих признаков применяются различные показатели, наиболее общим из них является коэффициент взаимной сопряженности Чупрова. Он применяется для сопряжения связи двух атрибутивных признаков, когда это варьирование образует 3 и более группы.

---

Пример, распределение 500 студентов заочников по оценкам на экзамене и характеру работы.

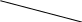Характер работы Оценки	По специальности	Не по специальности	Итого
Отлично	50	25	75
(в квадрате)	2500	625	0,15
(делим на итог)	7,1429	4,1666	11,3095
Хорошо	110	40	150
(в квадрате)	12100	1600	0,30
(делим на итог)	34,5714	10,6666	45,238
Удовлетворительно	180	65	245
(в квадрате)	32400	4225	0,492
(делим на итог)	92,5714	28,1666	120,738
Неудовлетворит.	10	20	30
(в квадрате)	100	400	0,0984
(делим на итог)	0,2857	2,6666	2,9523
Итого	350	150	500

1,0436 – эта сумма за вычетом единицы называется показателем взаимной сопряженности и обозначается , тогда коэффициент Чупрова рассчитывается:
,

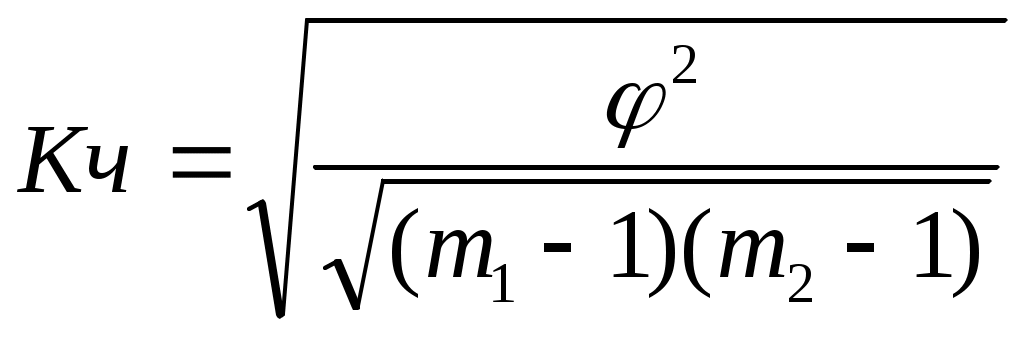где m – число групп по каждому признаку.
=0.1587
Кч изменяется от 1 до 0, но уже при значении 0,3 можно судить о тесной связи между вариацией изучаемых признаков.
Коэффициент ассоциации.

---

Если вариация обоих атрибутивных признаков ограничена двумя группами, то коэффициент Чупрова может быть определен проще, в виде коэффициента ассоциации. Для этого исходные данные сводятся в комбинированную четырех клеточную таблицу.

	1	2
1	a	b	a + b
2	c	d	c + d
	a + c	b + d

Ка рассчитывается по формуле:


Пример, распределение населения на городское и сельское по переписям.

Место жительства	39 г.			70 г.			89 г.
	г	н/г		г	н/г		г	н/г
Город	80,9	19,1	100	93,8	6,2	100	99,8	0,2	100
Село	50,6	49,4	100	84	16	100	99,5	0,5	100
	131,5	68,5		177,8	22,2		199,3	0,7

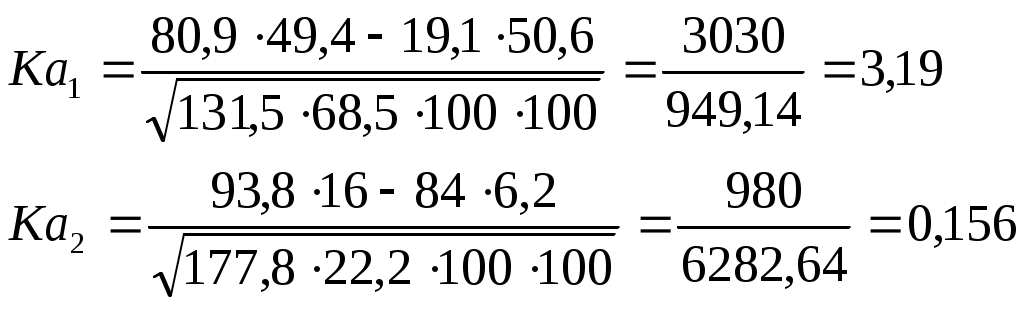
Ка изменяется от –1 до +1. Чем ближе он к крайним значениям, тем сильнее связаны между собой изучаемые признаки.

---

5. Метод сравнения параллельных рядов.
После того, как на основании теоретического анализа будет выявлено, что между изучаемыми явлениями существует взаимосвязь, необходимо выявить тесноту этой связи.

Это можно сделать с помощью параллельных рядов, для этого факторы, характеризующие результативный признак располагаются в возрастающем порядке, т.е. составляется ранжированный ряд, параллельно записываются признаки фактора.

Путем составления, расположенных таким образом рядов, определяются существенные связи и их направления.

Пример, уровни энерговооруженности (х) и производительности труда (у) по 15 заводам.

№ п/п	х	у	№ п/п	х	у	№ п/п	х	у
1	6,0	2	6	7,9	3	11	9,4	5
2	6,1	3	7	8,2	4	12	9,9	7
3	6,8	6	8	8,5	5	13	10,5	7
4	7,2	4	9	8,6	6	14	11,2	8
5	7,4	2	10	9,1	8	15	11,3	6

Рассматривая данные таблицы можно заметить, что с возрастанием признака х возрастает и признак у. Для сравнительного анализа параллельных рядов могут применяться элементарные показатели к которым можно отнести:

• 
  коэффициент Фехнера (К_ф), который оценивает связь на основе сравнения признаков с их средней арифметической.
  

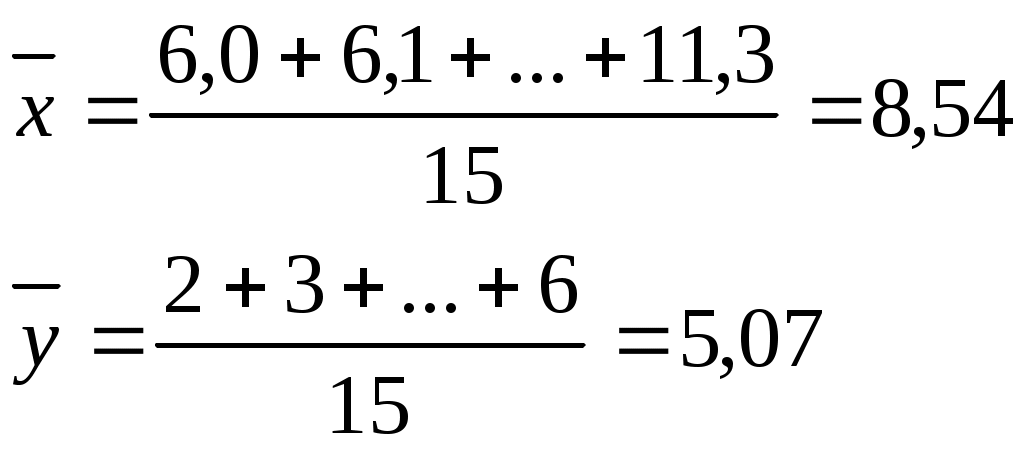
№ п/п	Знаки отклонений		№ п/п	Знаки отклонений		№ п/п	Знаки отклонений
	х	у		х	у		х	у
1	-	-	6	-	-	11	+	-
2	-	-	7	-	-	12	+	+
3	-	+	8	-	-	13	+	+
4	-	-	9	+	+	14	+	+
5	-	-	10	+	+	15	+	+

---

где С – число совпадений знаков х и у;

Н – число несовпадений знаков х и у
К_ф изменяются от +1 до –1. Если К_ф равен +1, то имеет место полностью согласованная прямая изменчивость.

Если коэффициент равен 0 – изменчивость не согласуется.

Если коэффициент равен –1, то полная обратная согласованная изменчивость.
- коэффициент корреляции рангов . он учитывает согласованность рангов, которые представлены в виде номеров, присвоенных единицам совокупности по каждому из признаков:

n – число единиц в совокупности;

d – разность рангов.
6. Метод аналитических группировок.
Значительно более сильно будет выделяться корреляционная зависимость, если применять метод группировки и сравнивать не индивидуальные значения, а групповые средние.

Такой прием единственно возможный, если нужно выявить зависимость на примере 100, 1000 единиц. При этом необходимо образовать такое количество групп, при котором в вариации групповых средних в максимальной степени будет проявляться влияние группировочного признака.

Чем больше групп образуется, тем больше увеличивается межгрупповая вариация, но при этом нельзя растягивать группировку, особенно при небольшом числе наблюдений. В этом случае группы получаются малочисленные и средние из них будут носить случайный характер, а межгрупповая вариация будет отражать не только влияние фактора признака, но и других факторов. Следовательно, нужно выбрать оптимальное число групп для конкретного случая, чтобы групповые средние перестали носить случайный характер и с каждой новой группой имели тенденцию к росту или снижению.

Составим группировку, состоящую из 4 групп: по энерговооруженности

Группы	х	у		Группы	у
6,0-7,325	26,1	15	3,75	6,0-7,1	11	2,2
7,33-8,65	32	14	3,5	7,1-8,2	9	1,8
8,65-9,98	37	26	6,5	8,2-9,3	23	4,6
9,98-11,31	33	21	5,25	9,3-10,4	12	2,4
		76	19		55	11

---