Файл: Методические указания к практическим работам по дисциплине б 16 Инженерная геодезия для направления 08. 03. 01 Строительство.docx

В геодезических расчетах знак суммы часто обозначают квадратными скобками [ ].


Задание 4. Обработка ряда равноточных измерений с применением формулы Бесселя
В соответствии с вариантом в приложении обработать результаты равноточных измерений угла наклона (число измерений n = 5):

3.1. Вычислить вероятнейшее значение измеренной величины (среднее арифметическое) - х_o . Для упрощения вычислений использовать способ «ложного нуля». Для этого наименьшее значение принимают за начало отсчета и вычисляют отклонения от наименьшего значения ε = х_i - х_min. Затем определяют вероятнейшее значение:

х_o = х_min + [ε] / n , где [ε] - сумма отклонений от наименьшего.

3.2. Вычислить среднюю квадратическую погрешность измерения - m ;

В таблице буквой δ обозначена вероятнейшая погрешность х_i - х_o (за истинное значение принято среднее арифметическое значение измеренной величины). Записать и использовать формулу Бесселя:
m =
3.3. Оценить точность определения среднего арифметического значения вычислением его средней квадратической погрешности М.

Номер изм-я	Угол хi	ε мин.	δ мин.	δ2	Средние квадратические погрешности, мин.
1
2					m =
3
4					M =
5

---

x_min=

[ε]=


[ε]/n= [δ]= [δ²]= x_o=
Задание 5. Оценка точности двойных равноточных измерений
С применением нивелира измерено шесть превышений по черным ( h ) и красным ( h' ) сторонам реек. Результаты измерений в виде статисти-ческого ряда двойных равноточных измерений сведены в таблицу. По этим данным вычислить среднеквадратическую погрешность m_h измерения превышения на станции по односторонним отсчетам, то есть каждого превышения.

Номер измерения	h, мм	h', мм	d, мм	d2
1	640	635
2	465	472
3	-370	-364
4	-865	-870
5	145	143
6	670	670

[d] = [d²] =

m_h =


Задание 6. Определение среднеквадратической погрешности функции измеренных величин
Задание 6.1. Вычислить площадь S прямоугольного участка на местности со сторонами а = 30,15 м и b = 40,09 м, а также и ее СКП, если размеры участка получены рулеткой с относительной погрешностью 1/1500. S = ab =

Записать выражение в общем виде для СКП:
m_s = ± √(dS/da)²*(m_a)²+(dS/db)²*(m_b)²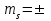

---

Вычислить частные производные по аргументу а и аргументу b:

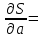
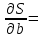
Вычислить СКП аргумента а и СКП аргумента b , используя понятие относительной погрешности: 1/N = 1/1500=m_a / a; 1/N= 1/1500 = m_b / b .

m_a= m_b =

Подставить числовые данные в выражение для m_s – средней квадратической погрешности измеренной площади прямоугольника:
m_s = ± √
Записать результат вычислений в виде: S = a*b ± m_s =

Задание 6.2 При определении высоты объекта Н теодолитом были измерены углы наклона на верхнюю и нижнюю точку сооружения υ_в = +25^о и υ_н = -5^о10^' cо средней квадратической погрешностью ± 0,2^’, а также измерено расстояние до сооружения d = 70м с относительной погрешностью 1/5000. Определить высоту объекта и ее СКП.

h₁

H

υ_в d

υ_н h₂
При вычислениях нужно использовать формулы тригонометрического нивелирования: Н = h₁+ h₂ = d tg υ_в + d tg υ_н.

Для первого и второго слагаемого в формуле Н получено выражение квадрата погрешности, которое следует поочередно применить к расчету:

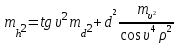, где

ρ´ = = ; m_υ = , m_d =
m_h = m_h1 + m_h2 =

Задание 7. Обработка неравноточных измерений

Обработать результаты определения высоты точки, полученной по четырем ходам.

Для определении весов отметок разных нивелирных ходов принимают вес каждого из результатов обратно пропорционально количеству превышений (штативов, станций) либо обратно пропорционально длине хода. В данной задаче для каждого хода рекомендуется принять вес р_i = 1 / n_i , где n_i – число превышений в ходе.

По примеру обработанной ведомости в соответствии с вариантом, дающим числа превышений в ходе, выполнить соответствующие вычисления. Использовать формулы, приведенные в приложении. При расчете среднего весового использовать «ложный нуль».
Пример обработки:

---

Высота	Число	Вес	δi = Hi - xo	pi δi	pi δi2
точки Нi , м	превы-	pi=1/ni	мм	мм
	шений ni
254, 383	4	0,25	2	0,5	1
, 379	2	0,5	-2	-1	2
, 385	3	0,33	4	1,3	5,2
, 378	5	0,2	-3	-0,6	1,8

					[p] = 1,28		[p δ] = 0,2	[p δ2] =10,0
Ho = 254,300 - -ложный нуль		[px] / [p] =				(0,25*83+ 0,5*79	+ 0,33*85 + 0,2*78) / 1,28 = 81, 2 мм.
хi = (Hi –Ho),мм			xо= Ho +			[px] / [p] = 254,381 м - среднее		весовое
						ω = 0,2 мм - погрешность округления xо
контроль вычислений:				ω[p] = 0,2·1,28 = 0,26 - примерно равно [p δ] и примерно равно нулю.

---

		- погрешность единицы веса, мм
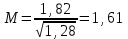		- средняя квадратическая погрешность весового среднего (мм)
Ведомость обработки ряда неравноточных измерений по варианту:
Высота			Число	Вес	δi = Hi - xo	pi δi		pi δi2
точки Нi , м			превы-	pi=1/ni	мм	мм
			шений ni
254, 383
, 379
, 385
, 378

---