Файл: Методические указания к практическим работам по дисциплине б 16 Инженерная геодезия для направления 08. 03. 01 Строительство.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 220
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Саратовский государственный технический университет
имени Гагарина Ю.А.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим работам
по дисциплине Б 1.1.16 «Инженерная геодезия»
для направления 08.03.01 «Строительство»,
профиль 1 «Производство строительных материалов, изделий и конструкций»
очная форма обучения

Саратов – 2021
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 3
1. ПР №1 «ОЦЕНКА ТОЧНОСТИ ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ» 4
1.1. Общие сведения 4
1.2. Основные формулы оценки точности равноточных измерений 7
1.3. Основные формулы оценки точности неравноточных измерений 8
1.4. Задания 9
1.5. Приложения 16
2. ПР №2 «ТЕОДОЛИТНАЯ СЪЕМКА» 20
2.1. Общие сведения 20
21
2.2. Задания 21
3. ПР №3 НИВЕЛИРОВАНИЕ ПОВЕРХНОСТИ (обработка материалов нивелирования по квадратам) 31
3.1. Общие сведения 31
3.2. Задания 34
3.3. Приложения 36
4. ПР №4 «НИВЕЛИРОВАНИЕ ТРАССЫ» (обработка журнала нивелирования трассы автодороги) 41
4.1 Задания 41
4.2. Приложения 44
СПИСОК ЛИТЕРАТУРЫ 49
ВВЕДЕНИЕ 3
1. ПР №1 «ОЦЕНКА ТОЧНОСТИ ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ» 4
1.1. Общие сведения 4
1.2. Основные формулы оценки точности равноточных измерений 7
1.3. Основные формулы оценки точности неравноточных измерений 8
1.4. Задания 9
1.5. Приложения 16
2. ПР №2 «ТЕОДОЛИТНАЯ СЪЕМКА» 20
2.1. Общие сведения 20
2.2. Задания 21
3. ПР №3 НИВЕЛИРОВАНИЕ ПОВЕРХНОСТИ (обработка материалов нивелирования по квадратам) 31
3.1. Общие сведения 31
3.2. Задания 34
3.3. Приложения 36
4. ПР №4 «НИВЕЛИРОВАНИЕ ТРАССЫ» (обработка журнала нивелирования трассы автодороги) 40
4.1 Задания 40
4.2. Приложения 43
СПИСОК ЛИТЕРАТУРЫ 47
ВВЕДЕНИЕ
Каждая из 4-х практических работ занимает 4 часа аудиторного времени. Результаты работ оформляются в рабочей тетради с использованием бланков, приведенных в заданиях к методическим указаниям.
Студенты должны знать основные виды погрешностей измерений, основные формулы расчета случайных погрешностей, что возможно только после решения и усвоения практических задач, которые приведены в заданиях к практическим работам по теме «Оценка точности геодезических измерений».
При выполнении работы «Теодолитная съемка»
студенты обрабатывают полевой журнала угловых измерений и заполняют ведомость координат. Обработка ведомости координат предусматривает предварительное вычисление дирекционных углов для 5 сторон полигона и решение прямой геодезической задачи для вычисления координат опорных точек.
В методические указания к практической работе «Нивелирование поверх-ности» включены краткие сведения о нивелировании поверхности, после которых излагается способ обработки результатов геометрического нивелирования участка по квадратам, приводятся расчетные формулы и даются необходимые пояснения для построения плана вертикальной съемки.
Практическая работа «Нивелирование трассы (обработка журнала технического нивелирования)» состоит из двух заданий: обработка журнала нивелирования, в который внесены данные по нивелированию трассы; расчет главных точек круговой горизонтальной кривой относительно вершины угла поворота, отмеченного в пикетажной книжке. В рабочей тетради прикладываются материалы обработки, выполненные по своему варианту: расчет главных точек круговой кривой с указанием варианта и журнал нивелирования.
1. ПР №1 «ОЦЕНКА ТОЧНОСТИ ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ»
1.1. Общие сведения
Цель работы – освоение учащимися способов определения погрешностей измерений, оценка влияния погрешностей на полученные результаты измерений. На выполнение заданий отводится 4часа.
Как бы тщательно не выполнялось измерение и как бы ни были совер-шенны инструменты измерений, всякое измерение неизбежно сопровождается погрешностью. Любое измерение имеет так называемую истинную погрешность измерения:
Δi = li - X ,
где li - результат измерения, Х - истинное значение измеряемой величины.
Точность измерений можно увеличить двумя способами:
- применением более точных, более совершенных приборов,
- измерением одной и той же величины несколько раз для того, чтобы исключить грубые и уменьшить систематические и случайные погрешности.
Критерии оценки точности измерений:
1.Средняя погрешность θ - вычисляется как среднее арифметическое из абсолютных значений погрешностей:
θ =
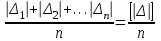
Эта величина не является надежным критерием особенно при коротком ряде наблюдений, потому что она не дает представления о разбросе значений ряда относительно средней величины ряда измерений (в статистике – относительно «математического ожидания»).
2. Вероятная погрешность r - такое значение случайной погрешности в данном ряду измерений, по отношению к которому одинаково возможны погрешности как больше этого значения по модулю, так и меньше. Если погрешности расположить в порядке возрастания, или убывания то вероятная погрешность будет находиться в середине ряда. В теории вероятностей доказано, что вероятная погрешность связана со средней квадратической погрешностьюm соотношением: r = 2 m / 3 = 0.67 m .
3. Средняя квадратическая погрешность m - погрешность, квадрат которой равен среднему арифметическому из суммы квадратов истинных случайных погрешностей:
m² =
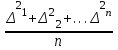 или m =
или m = 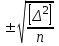
Эта погрешность Гаусса лучше, чем средняя погрешность, характеризует точность измерений, хорошо отражает степень отклонения от среднего значения ряда, то есть хорошо характеризует разброс значений относительно среднего, дисперсию ряда. Доказано, что для геодезических измерений можно ограничиться числом измерений n = > 8 . При этом величина m будет удовлетворять требуемой точности. Этот критерий принят в качестве основного в России.
Предложенная выдающимся математиком Гауссом формула для оценки точности предусматривает использование случайных истинных погрешностей, тогда как на практике чаще нам неизвестно истинное значение, которое входит в формулу Δi = li -X. В качестве истинного значения принимается арифметическая средина хо, и в расчете используется так называемая вероятнейшая погрешность δi = li - хo . В этом случае должна быть использована формула Бесселя : m =
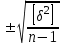 .
.4. Предельная погрешность Δпр связана с величиной m. Из теории ошибок следует, что случайная погрешность может превышать по модулю удвоенную среднюю квадратическую погрешность только в 5 случаях из 100 и утроенную в 3 случаях из 1000. Следовательно, почти невероятно, чтобы случайная погрешность измерения превысила утроенную величину
m. Поэтому эту величину и считают предельной, то есть: Δпр = ± 3 m . Для ограниченного числа измерений и в том случае, когда требования к точности принимаются более жесткими, принимают Δпр = ± 2 m.
Все рассмотренные погрешности - истинные, средние, средниеквадра-тические, вероятные и предельные являются абсолютными погрешностями и имеют размерность измеренных величин. Каждая из них находит применение в практике. В разных странах предпочтение отдается какой-то одной. В России чаще всего используют среднюю квадратическую погрешность.
Однако, все абсолютные погрешности иногда оказываются недостаточными (иначе говоря, слабыми) при оценке точности. Для более точной оценки точности бывает необходимо соотнести абсолютную погрешность измерения с измеренным значением.
5. Относительная погрешность - отношение какой-либо из абсолютных погрешностей к принятому результату измерения. Выражается эта погрешность в виде простой дроби с единицей в числителе:
fотн =
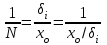 ;
; 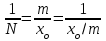 ;
; 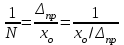
Соответствующие инструкции регламентируют допустимые относительные погрешности. Например, при измерении расстояний 20-метровой стальной лентой:
- для благоприятных условий измерений - 1 / 2000;
- для неблагоприятных условий (высокая растительность, много неровностей или камней) - 1 / 1000.
- для некоторых условий измерений принимают 1/1500.
Выполнив измерения, вычисляют фактические относительные погрешности и сравнивают их с допустимыми.
Относительная погрешность служит мерой для предварительной оценки точности измерений. Например, при измерениях с относительной погрешностью 1/2000 абсолютная погрешность в виде средней квадратической погрешности (СКП) не должна превышать 5 см на каждые 100м и 10 см на 200м.
Почти все геодезические измерения оцениваются относительной погрешностью, кроме угловых измерений, погрешность которых не зависит от величины измеренного угла. Однако, иногда приходится иметь дело с оценкой совместных измерений (как угловых, так и линейных), когда надо сопоставить влияние угловой и линейной составляющей на точность совместных измерений. Тогда используют и понятие относительной погрешностиизмерения угла (направления),
за которую принимают простую безразмерную дробь:
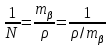 .
.Измерения, выполненные в условиях, при которых результаты можно считать одинаково надежными, то есть измерения одним и тем же мерным прибором или приборами одинаковой точности, исполнителями одинаковой квалификации и при одинаковых внешних условиях называются равно-точными. В противном случае измерения признаются неравноточными.