Файл: Курсовая работа по дисциплине Прогнозирование эксплуатационной надежности автотранспортных средств.docx
Добавлен: 17.01.2024
Просмотров: 90
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования РФ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Волгоградский Государственный технический университет»
Факультет автомобильного транспорта
Кафедра «Техническая эксплуатация и ремонт автомобилей»
Курсовая работа
по дисциплине «Прогнозирование эксплуатационной надежности автотранспортных средств»
Тема: «Составление вероятностной модели распределения наработки технического объекта с целью возможности дальнейшего прогнозирования отказов и выработки ресурса»
Выполнил: ст.гр. ТЭРА-2Н
Матрёнин В.В.
Номер зачетной книжки: 19102033
Проверил: доцент
Чернышов К.В.
Волгоград, 2020
Оглавление
Исходные данные………………………………………………………………….3
Этап 1. Определение закона распределения наработки, основных функциональных зависимостей распределения наработки и показателей надежности первого элемента……………………………………………………4
Этап 2. Определение основных функциональных зависимостей и показателей надежности остальных элементов технического объекта……………………..24
Этап 3. Определение функции надежности технического объекта в целом и вероятности отказа объекта за время t* по структурной схеме надежности…37
Исходные данные
Таблица 1 - Исходные данные (Вариант 13)
| | Номер элемента | t* | |||||||||||||||||
| 1 | 2 | 3 | 4 | ||||||||||||||||
| Время наблюдения 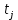 , мес | 1,5 | 3,0 | 4,5 | 6,0 | 7,5 | 9,0 | 10,5 | 12,0 | 13,5 | - | n | Вейб | Эксп | Норм | 3 | ||||
| Число отказов 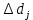 | 5 | 23 | 22 | 20 | 12 | 10 | 2 | 1 | 1 | - | 100 | 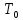 2 | 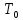1 | 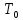2 | |||||
| Число приостановок 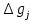 | 0 | 1 | 0 | 2 | 1 | 0 | 1 | 0 | 0 | - | 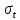 1,5 | 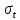1 | 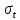2,5 | ||||||
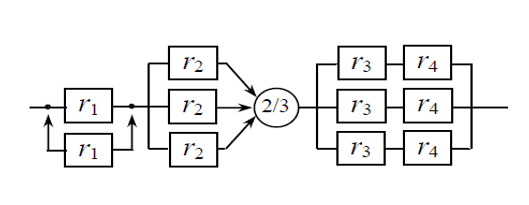
Рисунок 1 – Структурная схема надежности
Этап 1. Определение закона распределения наработки, основных функциональных зависимостей распределения наработки и показателей надежности первого элемента
Для построения графиков зависимостей заполним таблицу, где
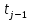и 
соответственно левая и правая границы j-го интервала времени,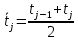 
- середина j-го интервала, 
– количество отказавших объектов в j-м интервале времени, 
- количество объектов, выбывших из испытаний по каким-либо причинам в j-м интервале времени,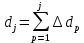 
- суммарное количество отказов от начала испытаний до конца j-го интервала времени,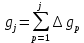 
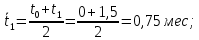
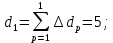
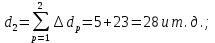
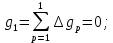
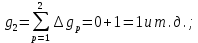
Эти величины являются исходными, подлежащими обработке.
Для определения необходимых зависимостей используем метод Джонсона. Для каждого интервала определяется суммарное прогнозируемое количество отказов по формуле
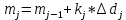
где
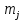– прогнозируемое количество отказов к концу предыдущего интервала (для первого интервала 
); 
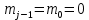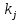– коэффициент приращения отказа в j-м интервале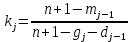
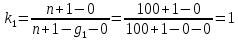
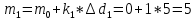
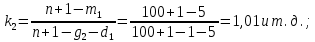
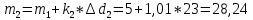
Далее вычислим прогнозируемое число отказов в каждом j-ом интервале
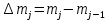
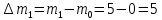
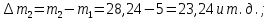
Зная значения
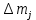определим статистическое значение вероятности отказа (относительную частоту отказа) в каждом j-м интервале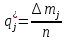
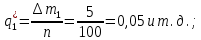
Таблица 2
 |  | |  | |  | |  |  |
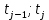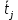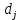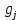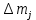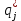| 0;1,5 | 0,75 | 5 | 5 | 0 | 0 | 5 | 5 | 0,05 |
| 1,5;3 | 2,25 | 23 | 28 | 1 | 1 | 23,24 | 28,24 | 0,2324 |
| 3;4,5 | 3,75 | 22 | 50 | 0 | 1 | 22,23 | 50,47 | 0,2223 |
| 4,5;6 | 5,25 | 20 | 70 | 2 | 3 | 21,05 | 71,53 | 0,2105 |
| 6;7,5 | 6,75 | 12 | 82 | 1 | 4 | 13,10 | 84,63 | 0,1310 |
| 7,5;9 | 8,25 | 10 | 92 | 0 | 4 | 10,92 | 95,54 | 0,1092 |
| 9;10,5 | 9,75 | 2 | 94 | 1 | 5 | 2,73 | 98,27 | 0,0273 |
| 10,5;12 | 11,25 | 1 | 95 | 0 | 5 | 1,36 | 99,64 | 0,0136 |
| 12;13,5 | 12,75 | 1 | 96 | 0 | 5 | 1,36 | 101 | 0,0136 |
Статистическую функцию распределения наработки строят на основании данных вариационного ряда по точкам, находящимся на границах интервалов этого ряда:
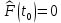
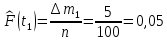
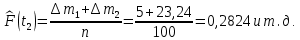
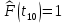
Таблица 3
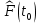 | 0 |
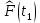 | 0,05 |
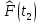 | 0,2824 |
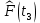 | 0,5047 |
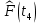 | 0,7153 |
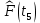 | 0,8463 |
Продолжение таблицы 3
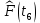 | 0,9554 |
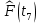 | 0,9827 |
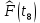 | 0,9964 |
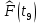 | 1 |
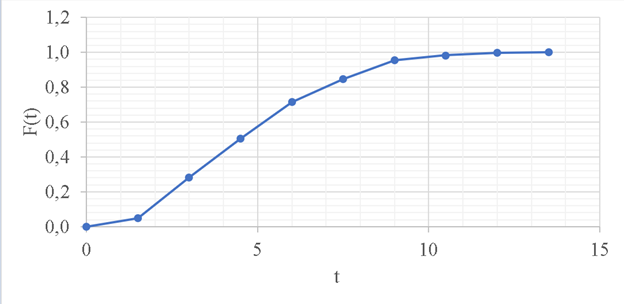
Рисунок 2 - График статистической функции распределения наработки
При построении статистической функции надежности определяют значения функции надежности на границах интервалов ряда:
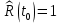
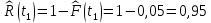
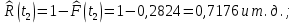
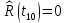
Таблица 4
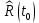 | 1 |
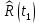 | 0,95 |
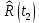 | 0,7176 |
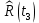 | 0,4953 |
Продолжение таблицы 4
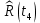 | 0,2847 |
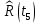 | 0,1537 |
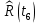 | 0,0446 |
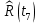 | 0,0173 |
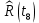 | 0,0036 |
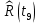 | 0 |
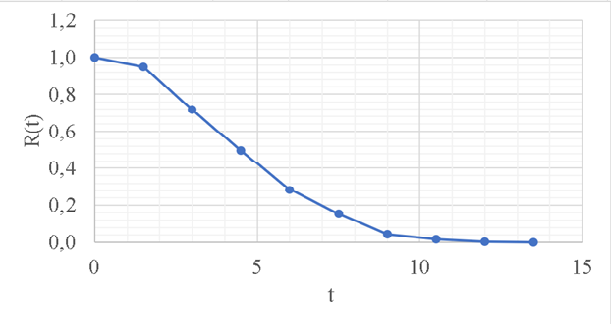
Рисунок 3 - График статистической функции надежности
Гистограмма представляет собой статистический график плотности распределения наработки и поэтому строится как производная от графика функции распределения. Высота расположения j-го отрезка определяется по формуле
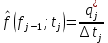
где
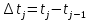– величина j-го интервала.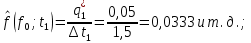
Таблица 5
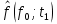 | 0,0333 |
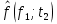 | 0,1549 |
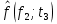 | 0,1482 |
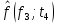 | 0,1404 |
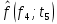 | 0,0873 |
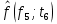 | 0,0728 |
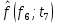 | 0,0182 |
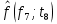 | 0,0091 |
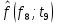 | 0,0091 |