Файл: Курсовая работа по дисциплине Прогнозирование эксплуатационной надежности автотранспортных средств.docx
Добавлен: 17.01.2024
Просмотров: 92
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
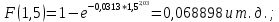
Таблица 8
| t |  |  |
| 0 | 0 | 0 |
| 1,5 | 0,0500 | 0,068 |
| 3 | 0,2824 | 0,252 |
| 4,5 | 0,5047 | 0,485 |
| 6 | 0,7153 | 0,695 |
| 7,5 | 0,8463 | 0,846 |
| 9 | 0,9554 | 0,933 |
| 10,5 | 0,9827 | 0,975 |
| 12 | 0,9964 | 0,992 |
Продолжение таблицы 12
| 13,5 | 1 | 0,997 |
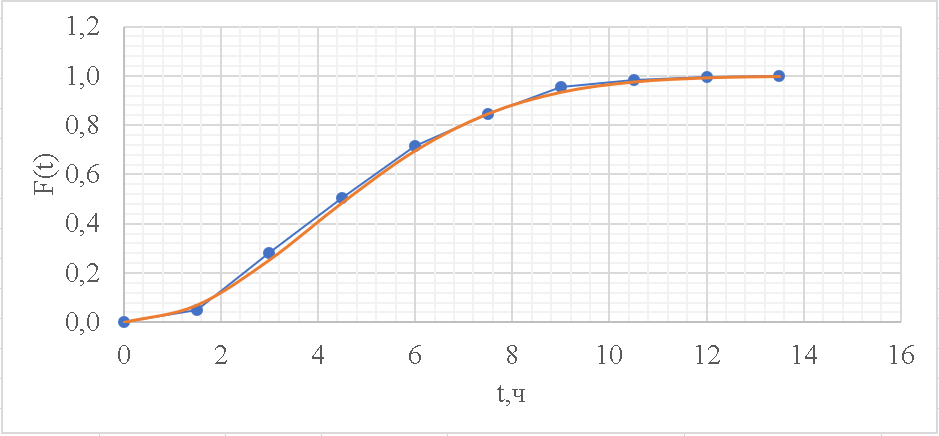
Рисунок 6 - Функция распределения наработки;
- ; 
- 
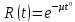
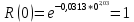
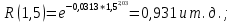
Таблица 9
| t |  |  |
| 0 | 1 | 1 |
| 1,5 | 0,95 | 0,931102 |
| 3 | 0,717 | 0,747106 |
| 4,5 | 0,495 | 0,514783 |
| 6 | 0,285 | 0,304 |
| 7,5 | 0,154 | 0,1536 |
| 9 | 0,045 | 0,066 |
| 10,5 | 0,017 | 0,0245 |
| 12 | 0,0036 | 0,007 |
| 13,5 | 0 | 0,002 |
Рисунок 7 - Функция надежности;
- ; - 
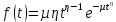
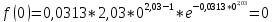
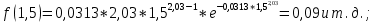
Таблица 10
| t |  |  |
| 0 | 0 | 0 |
| 1,5 | 0,0333 | 0,09 |
| 3 | 0,1549 | 0,1474 |
| 4,5 | 0,1482 | 0,1542 |
| 6 | 0,1404 | 0,1225 |
| 7,5 | 0,0873 | 0,0779 |
| 9 | 0,0728 | 0,0406 |
| 10,5 | 0,0182 | 0,0176 |
| 12 | 0,0091 | 0,0064 |
| 13,5 | 0,0091 | 0,0019 |
Рисунок 8 - Плотность распределения наработки;
- 
; - 
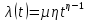
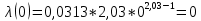
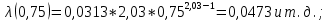
Таблица 11
| t |  |  |
| | - | 0 |
| 0,75 | 0,0342 | 0,0473 |
| 2,25 | 0,1858 | 0,1466 |
| 3,75 | 0,2444 | 0,2482 |
| 5,25 | 0,3599 | 0,3510 |
| 6,75 | 0,3983 | 0,4548 |
| 8,25 | 0,7339 | 0,5592 |
| 9,75 | 0,5881 | 0,6642 |
| 11,25 | 0,8690 | 0,7697 |
| 12,75 | 0,9724 | 0,8756 |
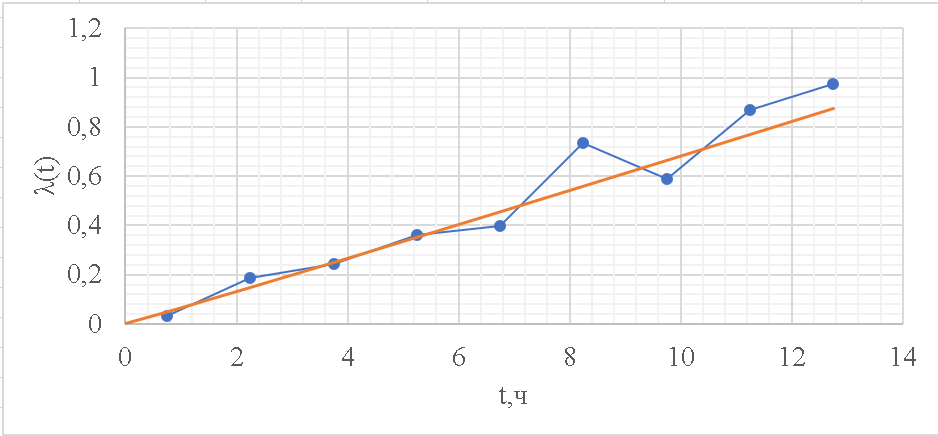
Рисунок 9 - Интенсивность отказов;
- ; - Оценим распределения Вейбулла с помощью критерия согласия Пирсона.
Для распределения Вейбулла
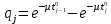
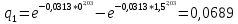
Таблица 12
 | 0,0689 |
 | 0,1840 |
 | 0,2323 |
 | 0,2108 |
 | 0,1503 |
 | 0,0873 |
 | 0,0419 |
 | 0,0168 |
 | 0,0057 |
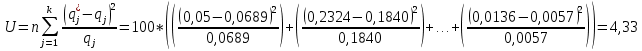
Для распределения Вейбулла
, тогда
Используя таблицу квантилей
определяем, что вероятность данного распределения 0,57.Большим уровнем значимости обладает распределение Вейбулла.
Этап 2. Определение основных функциональных зависимостей и показателей надежности остальных элементов технического объекта
Вторым элементом системы является распределение Вейбулла. Определим параметр формы и коэффициент масштаба
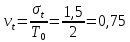
По таблице зависимости получаем
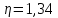
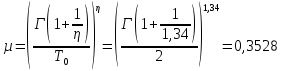
Основные функциональные зависимости:
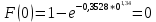
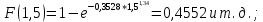
Таблица 17
| t | |
| 0 | 0 |
| 1,5 | 0,4552 |
| 3 | 0,7851 |
| 4,5 | 0,9292 |
| 6 | 0,9796 |
| 7,5 | 0,9947 |
| 9 | 0,9988 |
| 10,5 | 0,9997 |
| 12 | 0,9999 |
| 13,5 | 1 |
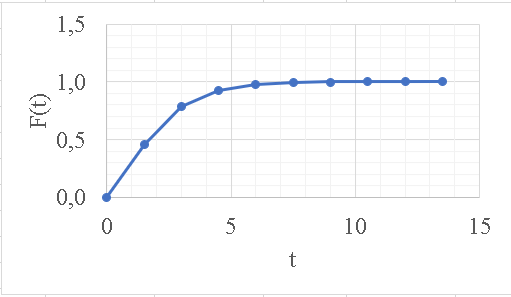
Рисунок 14 - Функция распределения наработки
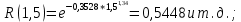
Таблица 13
| t | |
| 0 | 1 |
| 1,5 | 0,5448 |
| 3 | 0,2149 |
| 4,5 | 0,0708 |
| 6 | 0,0204 |
| 7,5 | 0,0053 |
| 9 | 0,0012 |
| 10,5 | 0,0003 |
| 12 | 0,0001 |
| 13,5 | 0,0000 |